Учебная презентация (сдвиг, срез, смятие)
реклама
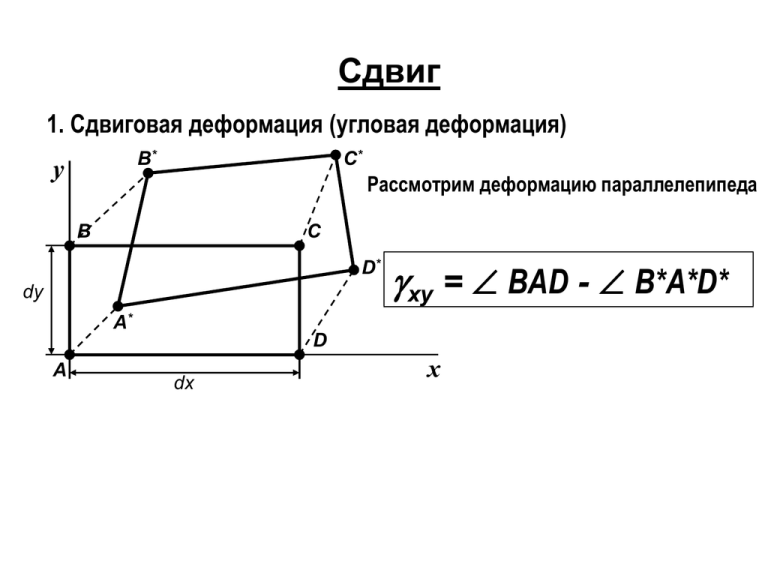
Сдвиг 1. Сдвиговая деформация (угловая деформация) В* y С* Рассмотрим деформацию параллелепипеда В С D* dy xy = BAD - B*A*D* А* D А dx x 2. Обобщенный закон Гука При воздействии x : y x x x E y y y ; y x y y ; x y x x x x z x x z x x x E x E Аналогично для других напряжений y ; y z y y y E E E z z z z z z z z z ; x z ; x z E E E 2. Обобщенный закон Гука Используя принцип суперпозиции: x = x x+ xy + xz = x E 1 x x ( y z ) E 1 y y ( x z ) E 1 z z ( x y ) E ( y E z E ) Обобщенный закон Гука для изотропного тела 2. Объемный закон Гука y Рассмотрим изменение объема единичного кубика: dy 1 V0 = 1 1 dz 1 z dx После деформации размеры кубика равны: x V1 = (1 + x)(1 + y)(1 + z) = x + y + z + x y + y z + z x + x y z =1+ Ввиду малости относительных деформаций (10-3…10-5) V1 = 1 + x + y + z; ΔV = ΔV1 – V0 = x + y + z V V x y z V0 2. Объемный закон Гука Используем обобщенный закон Гука: V = 1/E[x + y + z -n(y + z + x + z + x + y )] = (1 – 2n)/E (x + y + z) V = (1 – 2n)/E (x + y + z) Обозначим: Тогда: Обозначим: 0 = 1/3 (x + y + z) (1 2n )3 V 0 E E 3(1 2n ) Объемный закон Гука - среднее напряжение - объемный модуль упругости Видно, что nпред = 0.5 3. Сдвиг П клей заклепка П П сварка 3. Сдвиг Рассмотрим состояние т.н. чистого сдвига – прямоугольный элемент не испытывает удлинения сторон, на ┴ площадках действуют только Ранее было получено: +900 = xcos2 + sin2 - yxsin2 y y1x1 = ½(x - ) sin2 + yxcos2 y В нашем случае на исходных площадках: x = = 0, yx = - y = 0 при = 0, n/2 = sin2 (1) y1x1 = - cos2 Всегда = - +90 Закон «парности» нормальных напряжений при чистом сдвиге 3. Сдвиг Ранее было получено: 1 x x ( y z ) E 1 y y ( x z ) E 1 z z ( x y ) E Из (1): или 1 1 1 ( 2 3 ) E 1 2 2 ( 1 3 ) E 1 3 3 ( 1 2 ) E 1 > 2 > 3 max = при = 450 1 = , 2 = 0, 3 = - min = - при = - 450 3. Сдвиг Рассмотрим деформацию элементарного квадрата: y а А yx В ΔS В1 а 3 1 D = a 2 2 Δd = dAC = da 2 ΔS С1 Δd cos450 1 d 1 ( 3 ) 1 E E С С2 d Δd = C2C1 = ΔS x E 2(1 ) 3. Сдвиг Рассмотрим аналогию: E E G 2(1 ) G - модуль сдвига или «модуль упругости второго рода» 3. Сдвиг Полная сводка уравнений для пространственного напряженного состояния: 1 x x ( y z ) E 1 y y ( x z ) E 1 z z ( x y ) E xy yz zx xy G yz G zx G 4. Расчет заклепочных соединений «Внахлест» «Встык» Рассмотрим работу одной заклепки. Срез заклепки. Р Р Р Р Р Р P Р 2 d Аср n 4 где n – количество заклепок, d – диаметр заклепки R з ср где Rзср – расчетное сопротивление заклепки срезу 4P nср 2 з d Rср Смятие заклепки Условная поверхность смятия см Р з Rсм dtn t P nсм з dtRсм d Реально n = nmaxnср, nсм Разрушение основного материала t d d b N Aнетто P R t (b md ) Сварка hш 0.7hш P P Aш 0.7 hl0 l0










