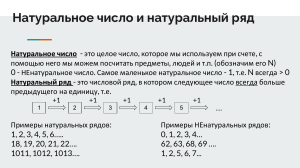
Задания отборочного тура юниорской олимпиады по математике 2013 -2014 учебный год

Задания отборочного тура юниорской олимпиады по математике
2013 -2014 учебный год
Первый уровень
1. На доске написано 30 последовательных натуральных чисел. Известно,
что сумма десяти из них – число простое. Может ли сумма оставшихся
20 чисел быть простым числом?
2. Найдите наименьшее натуральное число, произведение цифр которого
равно 2000.
3. В компании из 20 человек некоторые знакомы друг с другом.
Оказалось, что среди любых 13 человек этой компании число пар
знакомых одно и то же. Сколько всего пар знакомых может быть во
всей компании?
4. Из
шахматной
доски
8×8
вырезали
12
доминошек
(доминошка−прямоугольник 1×2). Верно ли что в оставшейся части
всегда можно вырезать прямоугольник 1× 3 ?
5. Если идти вниз по движущемуся эскалатору, то на спуск потратишь 1
минуту. Если увеличить собственную скорость в два раза, то
спустишься за 45 секунд. За какое время можно спуститься, стоя на
этом эскалаторе неподвижно?
Второй уровень
1. Площадь равностороннего треугольника, построенного на гипотенузе
прямоугольного треугольника, вдвое больше площади прямоугольного
треугольника. Найти меньший угол прямоугольного треугольника.
2. Найти три натуральных числа таких, что сумма всевозможных
двузначных чисел, составленных из этих цифр, равняется 231.
3. В куче лежит 75 спичек. Двое играющих берут по очереди от одной до
десяти спичек за ход. Взявший последнюю спичку получает
премиальный коробок с 60 спичками. Выигрывает тот, у кого с учетом
премии в сумме окажется больше спичек. Докажите, что начинающий
игрок может играть так, чтобы не проиграть, независимо от ходов
соперника.
4. Муравей находится в вершине проволочного куба и хочет попасть в
противоположную вершину, сделав ровно 5 «ходов» по ребрам.
Сколькими способами он может это сделать? (По одному ребру можно
ходить и несколько раз).
5. Двое по очереди ставят крестики в клетки доски размером
4×4.Проигрывает тот, после чьего хода образуется квадрат 2×2, в
каждой клетке которого стоит крестик. Кто выиграет: начинающий
или его партнер, и как нужно играть, чтобы выиграть?
Третий уровень
1. Найти наименьшее натуральное n , такое, что 2n можно представить в
виде суммы пяти различных простых чисел.
2. Десятичная запись некоторого натурального числа содержит 2013
единиц, 2013 двоек, 2013 четверок и столько же нулей. Может ли
такое число быть четвертой степенью натурального числа?
3. Числа от 1 до 12 разбили на две группы по шесть чисел в каждой.
Пусть A и B произведение чисел в каждой группе. Известно, что A
𝐴
делится на B .Найти все возможные значения .
𝐵
4. Сколько решений имеет уравнение
𝑥[𝑥]{𝑥}=a, 0<a<1,
если 0 < x < 2013.
5. Сколько существует двадцатизначных натуральных чисел таких, что
если его цифры записать в обратном порядке, то полученное число
будет ровно в три раза больше первоначального.