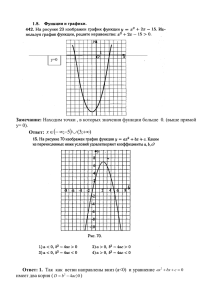
Даны вершины треугольника АВС
реклама

Даны вершины треугольника АВС. Составить уравнения медианы, высоты угла А, а также
уравнения прямых, проходящих через вершины треугольника и параллельных его
сторонам.
А(1; -1), В(4; 0); С (-2; 3).
Решение
1) Точка Е лежит между точками С и В, следовательно, ее координаты равны полусумме
координат этих точек Е(1; 3/2). По точкам А и Е проводим медиану - прямую АЕ:
x xA
y yA
y ( 1)
x 1
x 1 y 1
AE :
;
;
; x-1=0
xE x A yE y A
1 1 3 / 2 ( 1)
0
5/ 2
АЕ: x-1=0.
2) Найдем вектор СВ ={xВ-xС;yВ-yС}={ 4-(-2); 0 -3} = {6;-3}. Используем координаты точки
А(1; -1) и вектор СВ ={6;-3} как вектор нормали, находим уравнение высоты АД:
АД: 6(х-1)-3(y-(-1))=0; 6х-6-3y-3=0; 6x-3y-9=0
АД: 2х-y-3=0;
3) Найдем уравнения сторон:
x xA
y yA
AB :
;
xB x A yB y A
x 1 y ( 1)
x 1 y 1
;
; x-1=3y+3
4 1 0 ( 1)
3
1
АВ: x-3y-4=0.
x xA
y yA
y ( 1)
x 1
x 1 y 1
AС :
;
;
; 4x-4=-3y-3
xС x A yС y A
2 1 3 ( 1)
3
4
АС: 4x+3y-1=0.
x xB
y yB
x4
y 0
x4 y
BС :
;
;
; 3x-12=-6y
x С xB y С yB
24 30
6
3
ВС: x+2y-4=0.
Уравнения прямых, проходящих через вершины треугольника и параллельных его
сторонам, будут отличаться от полученных уравнений свободным членом, который
определим, подставляя координаты соответствующей вершины.
а) Параллельно АВ
x-3y+F=0, подставляя координаты С(-2; 3), получаем:
-2-3*3+F=0 или F=11,
Следовательно, искомое уравнение имеет вид: x-3y+11=0
б) Параллельно АС
4x+3y+F=0, подставляя координаты В( 4; 0), получаем:
4*4+3*0+F=0 или F=-16,
Следовательно, искомое уравнение имеет вид: 4x+3y-6=0
c) Параллельно ВС
x+2y+F=0, подставляя координаты А(1; -1), получаем:
1+2*(-1)+F=0 или F=1,
Следовательно, искомое уравнение имеет вид: x+2y+1=0