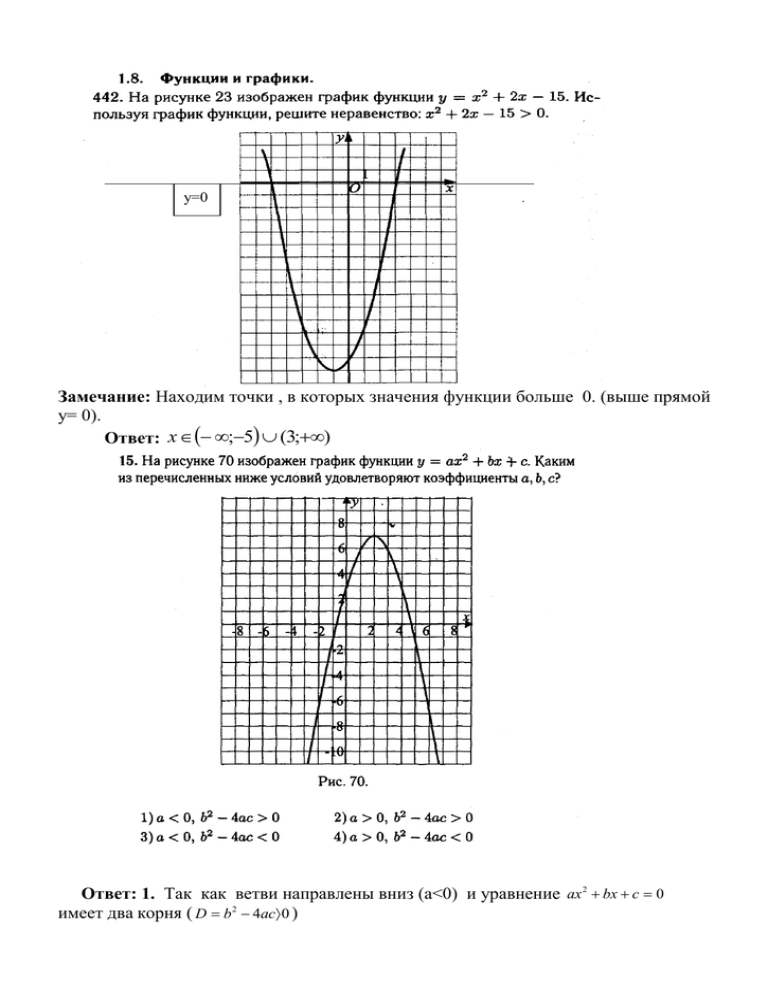
  ) ;

y=0
Замечание: Находим точки , в которых значения функции больше 0. (выше прямой
у= 0).
Ответ: x   ;5  (3;)
Ответ: 1. Так как ветви направлены вниз (а<0) и уравнение ax 2  bx  c  0
имеет два корня ( D  b2  4ac 0 )
Замечание: Область определения функции ( D(y) ) – это все значения переменной
х , которые определяются по графику функции.
Область значений функции ( E(y) ) – это все значения переменной у,
которые определяются по графику функции.
Ответ:
1)
А ; 2)
В ; 3)
Б
y=0
Замечание: Находим точки , в которых значения функции больше 0. (выше
прямой у= 0).
Ответ: x   3;1  2;4
Замечание: при нахождений нужного графика , подставляя значения
переменной х в заданные функций, определяем точки на координатной плоскости
и соответствующие графики.
Ответ: 1)
Б
; 2)
В
;
3)
А
у=-1
Замечание: Находим точки , в которых значения функции больше - 1. (выше
прямой у= - 1).
Ответ: x   3;1  1;4
Замечание: Определяем промежутки времени и пути ,пройденные за эти
промежутки и находим скорости в этих промежутках. Например, ВС=3 часам, а
путь 1 км, тогда скорость равна 1/3 км/час.
Ответ: Наибольшая скорость на промежутке времени АВ. ( 4 км/час.) .
Замечание: при нахождений нужного графика , подставляя значения
переменной х в заданные функций, определяем точки на координатной плоскости
и соответствующие графики.
Ответ: 1)
А
; 2)
В
;
3)
Б
Замечание: Решить систему уравнений , значит надо найти пару чисел ,
удовлетворяющей данной системе уравнений. Такие пары чисел определяют точки
пересечения графиков функций, т.е. их координаты.
В данном случае определяем координаты точек пересечения. Это точка (0;2), но
она есть на двух рисунках. При нахождений нужного графика , подставляя значения
переменной х в заданные функций, определяем точки на координатной плоскости
и соответствующие графики.
Ответ: график 1).
Решение:
Прямая y= k x + b проходит через точки А ( 1 ; 1 ) и В ( 0 ; 4 ). Напишите уравнение
этой прямой .Подставляем в уравнение прямой значения координат заданных точек
и получаем систему уравнении.
 1  k 1  b
1 k 4
b  4

k  3
4  k  0  b
y = k x +b ; подставляем значения k и b , и получаем уравнение прямой :
y  3 x  4
Ответ: y  3 x  4
Решение: 1) ветви направлены вниз , значит а<0.
2) точка пересечения с осью ОУ имеет координаты (0;-1).
-1=а*0+b*0+c
c = -1 отсюда с <0.
3) вершина ( -1,7;2) -1,7=-b/2a и а<0 , отсюда b<0. (m=-b/2a ; n=y(m)вершина)
Ответ : a<0 ; b<0; c<0.
Решение: Метод определения коэффициентов и свободного члена.
2
График функции y= ax  bx  c проходит через точки с координатами (-3;-5) , (1;-5) , (-2;-6).
Составим систему уравнений , подставляя координаты данных точек.
 9a  3b  c  5..............................

 a  b  c  5..........................
4a  2b  c  6  c  4a  2b  6

 a  (3) 2  b  (3)  c  5

2
 a  (1)  b  (1)  c  5
a  (2) 2  b  (2)  c  6

9a  3b  4a  2b  6  5
Подставляем в первые два уравнения. 
 a  b  4a  2b  6  5
 5a  b  1
 3a  b  1
Сложим эти два уравнения 
2а=2
а=1
9 1  3b  c  5
Подставляем значение а в первые два уравнения. 
1  b  c  5......
Вычтем из 1-го уравнения 2-ое. -2b=-8
b=4
Подставляем значения а и b в 1-ое уравнение 9*1-3*4+с=-5
с =-2
Отсюда следует a=1 b=4 c=- 2
1), 2), 3) не подходят при проверке. Значит ответ 4) является решением. (Ответ
виден из рисунка , x1  0,5.......x2  4,5 )
Ответ : 4).
2
Решение: График функции y= ax  bx  c имеет вершину (-2 ; -6 ). Отсюда
2
следует m=-2 n= -6 , а m=-b/2a
n= a(m)  b(m)  c
2
n= a(2)  b(2)  c
-2 = - b / 2a
- 6 = 4a – 2b+c
b= 4a
-6 = 4a -8a +c
c = 4a - 6
2
подставляем значения в выражение y= ax  bx  c .
- 6  a  - 2   4a  (2)  4a  6
 a 1
 b  4 1  4
 c  4  1  6  2
2
1), 2), 3) не подходят при проверке. Значит ответ 4) является решением. (Ответ
виден из рисунка , x1  0,5.......x2  4,5 )
Ответ : 4).
Замечание: Отсюда функция будет задана формулой.
2
y= ax  bx  c
y  1 x2  4x  2
y  x2  4x  2
Решение : выразим переменную у через переменную х для каждого уравнения
y  2x  2  y  2x  2
x 5

2 2
Найдем точку пересечения графиков этих функций , координаты которой являются
решениями данной системы уравнении : х = -3 у = -4 .
Ответ: ( -3 ; -4 )
2 y  x  5  2 y  x  5  y 
 x2  2x  3  0
Решение: Преобразуем неравенство
 ( x 2  2 x  1)  4  0
 ( x  1) 2  4  0.....  3
 ( x  1) 2  7  3
Находим промежуток , где график квадратичной функции выше прямой у=3 .
x   1;3 или – 1 < x < 3
Ответ: 3).
1
5
x
3
3
Умножаем обе части уравнения на 3 и
получаем уравнение 3у = х – 5 или
х – 3у = 5, т.е. получаем данную систему.
Решаем данную систему уравнении
графическим методом .( Решением системы
уравнении являются соответствующие
координаты точек пересечения этих
графиков). Такими точками будут точки с
координатами (0 ; 5 ) и (- 4 ; - 3 ). Отсюда
система уравнении имеет два решения.
Преобразуем уравнение y 
x1  0.................x2  4
y1  5................ y2  3
Ответ : ( 0 ; 5 ) и ( - 4 ; - 3 )
Замечание: при нахождений нужного графика , подставляя значения
переменной х в заданные функций, определяем точки на координатной плоскости
и соответствующие графики.
Графики функций параллельны , так как угловые коэффициенты у них равны 2.
И соответствуют рисунку А. ( система уравнении не имеет решения.)
Надо помнить , что уравнение прямой имеет вид y = kx + b , где k – угловой
коэффициент прямой и равен тангенсу угла наклона прямой к оси ОХ , k = tg 
1  острый... угол  tg1  0  k  0...(отрицат.)
 2  острый... угол  tg 2  0  k  0...(положит.)
Ответ: А.
Графики на ГИА…