ОРДЕНА ДРУЖБЫ НАРОДОВ РОССИЙСКИЙ УНИВЕРСИТЕТ ДРУЖБЫ НАРОДОВ
реклама
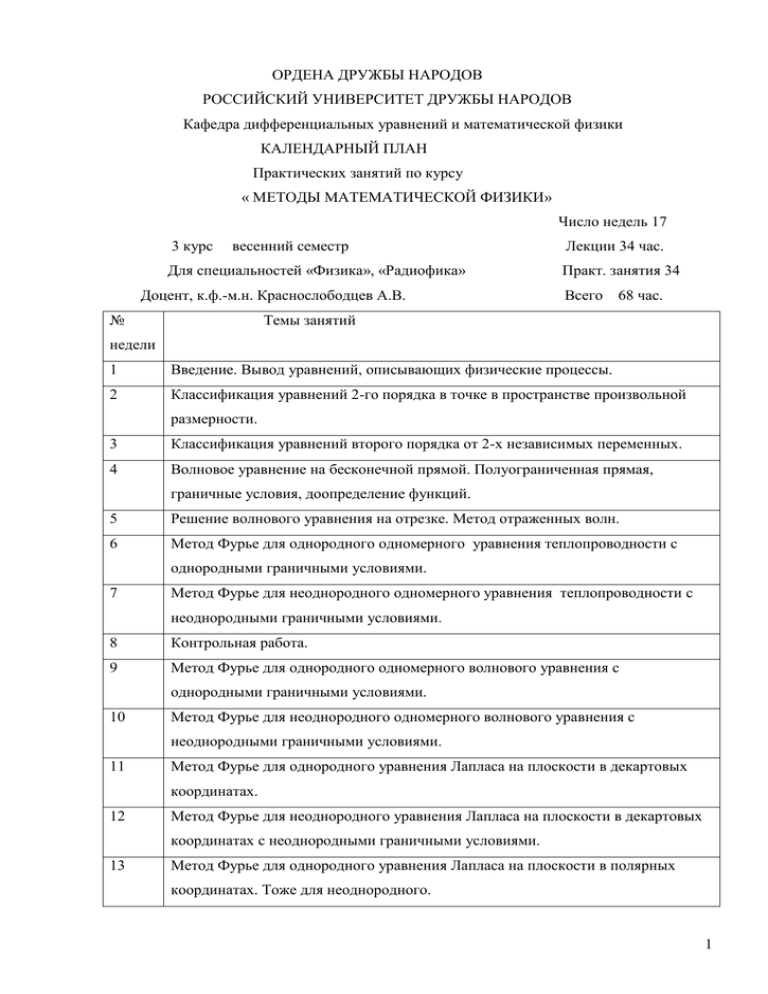
ОРДЕНА ДРУЖБЫ НАРОДОВ РОССИЙСКИЙ УНИВЕРСИТЕТ ДРУЖБЫ НАРОДОВ Кафедра дифференциальных уравнений и математической физики КАЛЕНДАРНЫЙ ПЛАН Практических занятий по курсу « МЕТОДЫ МАТЕМАТИЧЕСКОЙ ФИЗИКИ» Число недель 17 3 курс весенний семестр Для специальностей «Физика», «Радиофика» Доцент, к.ф.-м.н. Краснослободцев А.В. № Лекции 34 час. Практ. занятия 34 Всего 68 час. Темы занятий недели 1 Введение. Вывод уравнений, описывающих физические процессы. 2 Классификация уравнений 2-го порядка в точке в пространстве произвольной размерности. 3 Классификация уравнений второго порядка от 2-х независимых переменных. 4 Волновое уравнение на бесконечной прямой. Полуограниченная прямая, граничные условия, доопределение функций. 5 Решение волнового уравнения на отрезке. Метод отраженных волн. 6 Метод Фурье для однородного одномерного уравнения теплопроводности с однородными граничными условиями. 7 Метод Фурье для неоднородного одномерного уравнения теплопроводности с неоднородными граничными условиями. 8 Контрольная работа. 9 Метод Фурье для однородного одномерного волнового уравнения с однородными граничными условиями. 10 Метод Фурье для неоднородного одномерного волнового уравнения с неоднородными граничными условиями. 11 Метод Фурье для однородного уравнения Лапласа на плоскости в декартовых координатах. 12 Метод Фурье для неоднородного уравнения Лапласа на плоскости в декартовых координатах с неоднородными граничными условиями. 13 Метод Фурье для однородного уравнения Лапласа на плоскости в полярных координатах. Тоже для неоднородного. 1 14 Дифференцирование обобщенных функций. Замена переменных в обобщенных функциях. 15 Решение простейших алгебраических уравнений в обобщенных функциях. 16 Контрольная работа. 17 Повторение пройденного материала. Ведущий дисциплину Краснослободцев А.В. Зав. кафедрой Скубачевский А.Л. 2









