Учебно-тематические планы лекционных занятий по курсу

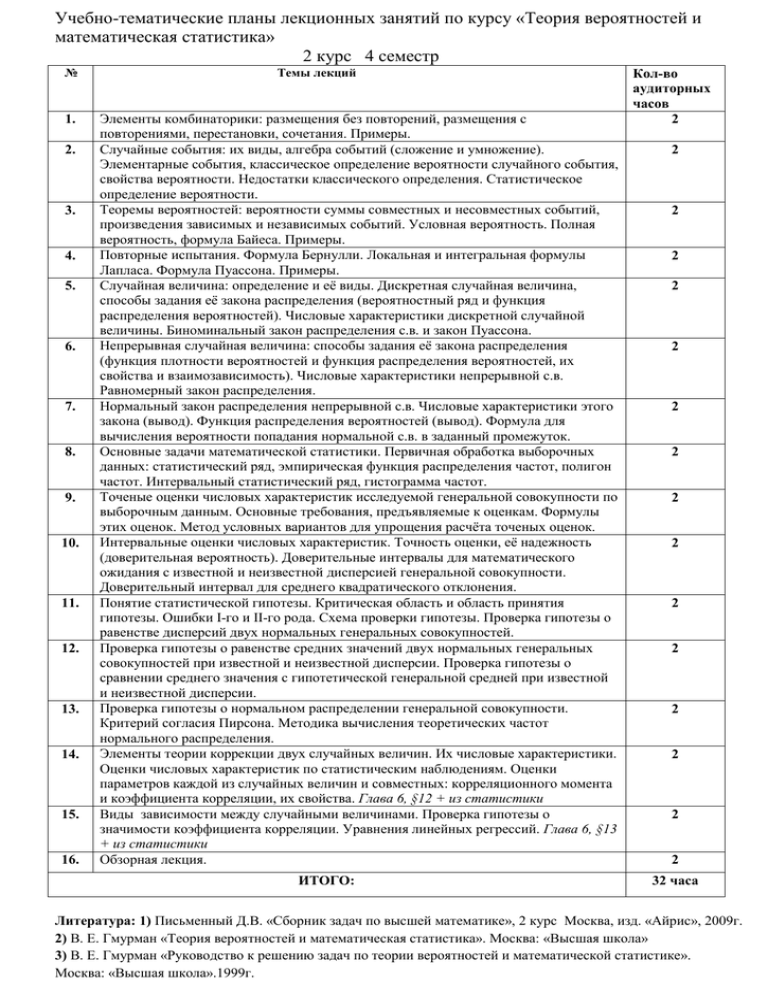
Учебно-тематические планы лекционных занятий по курсу «Теория вероятностей и
математическая статистика»
2 курс 4 семестр
№
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
Темы лекций
Элементы комбинаторики: размещения без повторений, размещения с
повторениями, перестановки, сочетания. Примеры.
Случайные события: их виды, алгебра событий (сложение и умножение).
Элементарные события, классическое определение вероятности случайного события,
свойства вероятности. Недостатки классического определения. Статистическое
определение вероятности.
Теоремы вероятностей: вероятности суммы совместных и несовместных событий,
произведения зависимых и независимых событий. Условная вероятность. Полная
вероятность, формула Байеса. Примеры.
Повторные испытания. Формула Бернулли. Локальная и интегральная формулы
Лапласа. Формула Пуассона. Примеры.
Случайная величина: определение и её виды. Дискретная случайная величина,
способы задания её закона распределения (вероятностный ряд и функция
распределения вероятностей). Числовые характеристики дискретной случайной
величины. Биноминальный закон распределения с.в. и закон Пуассона.
Непрерывная случайная величина: способы задания её закона распределения
(функция плотности вероятностей и функция распределения вероятностей, их
свойства и взаимозависимость). Числовые характеристики непрерывной с.в.
Равномерный закон распределения.
Нормальный закон распределения непрерывной с.в. Числовые характеристики этого
закона (вывод). Функция распределения вероятностей (вывод). Формула для
вычисления вероятности попадания нормальной с.в. в заданный промежуток.
Основные задачи математической статистики. Первичная обработка выборочных
данных: статистический ряд, эмпирическая функция распределения частот, полигон
частот. Интервальный статистический ряд, гистограмма частот.
Точеные оценки числовых характеристик исследуемой генеральной совокупности по
выборочным данным. Основные требования, предъявляемые к оценкам. Формулы
этих оценок. Метод условных вариантов для упрощения расчёта точеных оценок.
Интервальные оценки числовых характеристик. Точность оценки, её надежность
(доверительная вероятность). Доверительные интервалы для математического
ожидания с известной и неизвестной дисперсией генеральной совокупности.
Доверительный интервал для среднего квадратического отклонения.
Понятие статистической гипотезы. Критическая область и область принятия
гипотезы. Ошибки I-го и II-го рода. Схема проверки гипотезы. Проверка гипотезы о
равенстве дисперсий двух нормальных генеральных совокупностей.
Проверка гипотезы о равенстве средних значений двух нормальных генеральных
совокупностей при известной и неизвестной дисперсии. Проверка гипотезы о
сравнении среднего значения с гипотетической генеральной средней при известной
и неизвестной дисперсии.
Проверка гипотезы о нормальном распределении генеральной совокупности.
Критерий согласия Пирсона. Методика вычисления теоретических частот
нормального распределения.
Элементы теории коррекции двух случайных величин. Их числовые характеристики.
Оценки числовых характеристик по статистическим наблюдениям. Оценки
параметров каждой из случайных величин и совместных: корреляционного момента
и коэффициента корреляции, их свойства. Глава 6, §12 + из статистики
Виды зависимости между случайными величинами. Проверка гипотезы о
значимости коэффициента корреляции. Уравнения линейных регрессий. Глава 6, §13
+ из статистики
Обзорная лекция.
ИТОГО:
Кол-во
аудиторных
часов
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
32 часа
Литература: 1) Письменный Д.В. «Сборник задач по высшей математике», 2 курс Москва, изд. «Айрис», 2009г.
2) В. Е. Гмурман «Теория вероятностей и математическая статистика». Москва: «Высшая школа»
3) В. Е. Гмурман «Руководство к решению задач по теории вероятностей и математической статистике».
Москва: «Высшая школа».1999г.