Лабораторная работа №6 МО БородинМ

Министерство образования и науки Российской Федерации
Государственное образовательное учреждение высшего профессионального
образования
«Национальный исследовательский Томский политехнический университет»
Институт – Кибернетики
Кафедра – ИПС
ЛАБОРАТОРНАЯ РАБОТА № 6
«Линейное программирование»
Вариант №1
Выполнил
студент группы 8В83
М.С. Бородин
Проверил
О.В. Березняк
Томск 2011
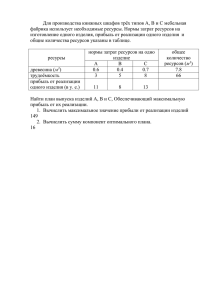
Задание
Для производства столов и шкафов мебельная фабрика использует
необходимые ресурсы. Нормы затрат ресурсов на одно изделие данного вида,
прибыль от реализации и общее количество имеющихся ресурсов каждого
вида приведены в следующей таблице:
Тип ресурса
Древесина I вида (куб. м)
Древесина II вида (куб. м)
Трудоемкость (человеко-часов)
Прибыль от реализации одного
изделия (тыс. руб.)
Нормы затрат ресурсов на
единицу продукции
стол
Шкаф
0.2
0.1
0.1
0.3
1.2
1.5
600
800
Наличие ресурсов
40
60
371.4
Определить, сколько столов и шкафов фабрике следует изготовить,
чтобы прибыль от их реализации была максимальной.
Ход работы
При выпуске продукции, на каждый товар тратится древесина разного
вида и рабочее время. Решение задачи сводится к определению числа
товаров обоих видов продукций так, чтобы ресурсы на их изготовление не
превышали имеющееся количество этих ресурсов. Также необходимо
выполнение основного условия – достижения максимальной прибыли.
Для решения составим систему неравенств. Примем за a и b искомые
количества произведенных товаров.
𝑎≥0
𝑏≥0
0.2 ∙ 𝑎 + 0.1 ∙ 𝑏 ≤ 40
0.1 ∙ 𝑎 + 0.3 ∙ 𝑏 ≤ 60
1.2 ∙ 𝑎 + 1.5 ∙ 𝑏 ≤ 371.4
{
Общая стоимость всей продукции описывается уравнением:
𝐹 = 600 ∙ 𝑎 + 800 ∙ 𝑏
Имеем задачу линейного программирования, заданную в стандартном
виде. Для решения надо систему представить в виде:
𝑎=0
𝑏=0
0.2 ∙ 𝑎 + 0.1 ∙ 𝑏 = 40
0.1 ∙ 𝑎 + 0.3 ∙ 𝑏 = 60
1.2 ∙ 𝑎 + 1.5 ∙ 𝑏 = 371.4
{
2
Имеем систему уравнений с двумя неизвестными. Систему можно
решить геометрическим способом. Каждое уравнение из системы
𝑎≥0
𝑏≥0
0.2 ∙ 𝑎 + 0.1 ∙ 𝑏 ≤ 40
0.1 ∙ 𝑎 + 0.3 ∙ 𝑏 ≤ 60
1.2 ∙ 𝑎 + 1.5 ∙ 𝑏 ≤ 371.4
{
представляет собой линию на плоскости aOb. Эта линии ограничивают
некоторые области. Построив их, получим геометрическую фигуру. После
этого нужно исследовать граничные точки, и затем можно будет сделать
вывод о наиболее эффективном количестве производимой продукции.
Можно сделать вывод, что оптимальное решение следует искать на
границе многогранника, ограниченного прямыми b1(a), b2(a), b3(a), a=0, b=0.
Вектор g указывает направление возрастания формы.
400
360
320
b1( a )280
b2( a )240
b3( a )
200
b4( a )
160
bx( a )
120
g
80
40
0
0
60
120
180
240
300
360
420
480
540
600
a
Рисунок 1 – График линий
Тогда при оптимальных значениях a и b получаем максимально
возможное значение прибыли F:
𝐹 = 600 ∗ 102 + 800 ∗ 166 = 194000
3
Для убеждения в правильности полученного результата, подтвердим
данные вычисления, вычислениями, проделанными в Mathcad.
2 1
M   1 3 


 12 15 
X  0
0
 400 
T   600 


 3714 
X  0
1
f ( X)  600 X  800 X
0
1
Given
X0
M X  T
G  Maximize( f X)
 102 

 166 
G
5
f ( G)  1.94  10
Вывод
В ходе лабораторной работы мы изучили принципы линейного
программирования на задаче об оптимальном плане выпуска продукции. Для
решения задачи был выбран геометрический метод, в котором мы
определяем решение в области допустимых значений, заданной тремя
прямыми. Двигаясь в направлении вектора g, мы получили оптимальные
значения x1 и x2, необходимые для достижения максимального значения F.
Отличие графического метода от дифференциальных состоит в том,
что графический позволяет находить значения на границах области. Это
необходимо при решении задач линейного программирования.
4