Примеры задач по теме «Основы термодинамики.... Задача: процесс, показанный на рисунке. За цикл... теплоты Q

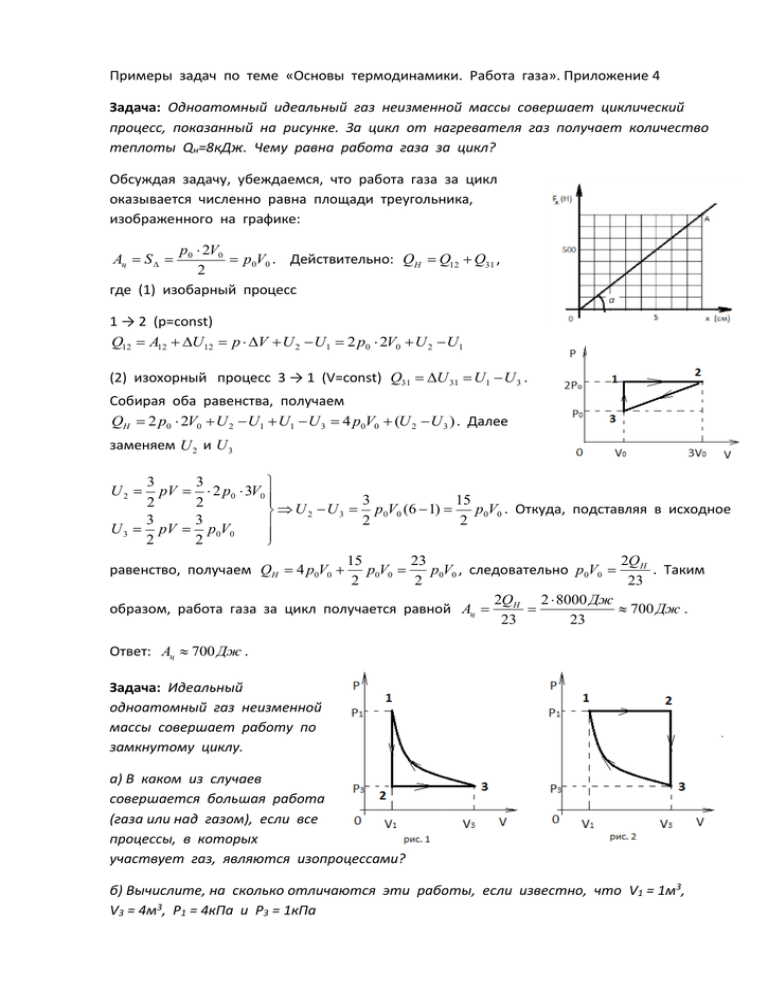
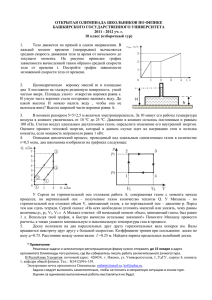
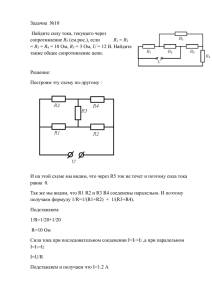
Примеры задач по теме «Основы термодинамики. Работа газа». Приложение 4
Задача: Одноатомный идеальный газ неизменной массы совершает циклический
процесс, показанный на рисунке. За цикл от нагревателя газ получает количество
теплоты Qн=8кДж. Чему равна работа газа за цикл?
Обсуждая задачу, убеждаемся, что работа газа за цикл
оказывается численно равна площади треугольника,
изображенного на графике:
p0  2V0
 p0V0 . Действительно: QH  Q12  Q31 ,
2
где (1) изобарный процесс
Ац  S  
1 → 2 (р=const)
Q12  A12  U12  p  V  U 2  U1  2 p0  2V0  U 2  U1
(2) изохорный процесс 3 → 1 (V=const) Q31  U 31  U1  U 3 .
Собирая оба равенства, получаем
QH  2 p0  2V0  U 2  U1  U1  U 3  4 p0V0  (U 2  U 3 ) . Далее
заменяем U 2 и U 3
3
3

pV   2 p0  3V0 
3
15

2
2
p0V0 . Откуда, подставляя в исходное
  U 2  U 3  p0V0 (6  1) 
3
3
2
2

U 3  pV  p0V0

2
2
2QH
15
23
p0V0 , следовательно p0V0 
равенство, получаем QH  4 p0V0  p0V0 
. Таким
23
2
2
2QH 2  8000 Дж

 700 Дж .
образом, работа газа за цикл получается равной Ац 
23
23
U2 
Ответ: Ац  700 Дж .
Задача: Идеальный
одноатомный газ неизменной
массы совершает работу по
замкнутому циклу.
а) В каком из случаев
совершается большая работа
(газа или над газом), если все
процессы, в которых
участвует газ, являются изопроцессами?
б) Вычислите, на сколько отличаются эти работы, если известно, что V1 = 1м3,
V3 = 4м3, Р1 = 4кПа и Р3 = 1кПа
а) Рассматривая графики изопроцессов, вспоминаем, что это отрезки в случае
изобарного и изохорного процессов и фрагмент гиперболы, если процесс
изотермный. Далее, рассуждая аналогично предыдущей задаче, получаем, что работа
за цикл численно равна площади замкнутого криволинейного треугольника,
ограниченного гиперболой на участке 1→3 и отрезками 1→2 и 2→3. Сравниваем
качественно площади двух треугольников, считая точки 1 и 3 одинаковыми на обоих
графиках и используя свойство выпуклости гиперболы, очевидно, получаем, что во
втором случае площадь внутри треугольника больше, значит работа, выполняемая
газом, также оказывается больше (рис.2).
Для ответа на вопрос (б) воспользуемся умениями, приобретенными учащимися
при изучении темы «Вычисление площадей с помощью интегралов» на уроках
алгебры 11 класса. Рассматриваем функции p  р(V ) , здесь при расчете работы над
4
(функция, задающая гиперболу при
V
изобарном процессе при условиях, что р (1)  4 и р (4)  1 ) и прямая р=1 (при
газом (рис. 1) используем функцию р 
изобарном процессе), где V изменяется от 1 до 4 (пределы интегрирования).
Получаем, что площадь в первом случае рассчитывается как определенный интеграл
4

S     1dV . Рассуждая аналогично, получаем интеграл для расчета площади
V

1
4
4

второго треугольника: S    4  dV . Проведя необходимые вычисления, получим
V
1
4
результат, записанный в кДж.
4
4 
Имеем S1     1dV  4 ln V V  1  4 ln 4  4  4 ln 1  1  4 ln 4  3 и
V

1
4
4
4

S 2    4  dV  4V  4 ln V  1  16  4 ln 4  4  4 ln 1  12  4 ln 4 . Разницу для двух
V
1
4
работ находим вычитанием 12  4 ln 4  (4 ln 4  3)  15  8 ln 4  4 . Получили, что при
заданных числовых условиях работа, совершаемая над газом (рис. 2) больше, чем
работа газа (рис. 1) на ≈ 4кДж.
Ответ: работа, совершаемая над газом больше на ≈ 4кДж.