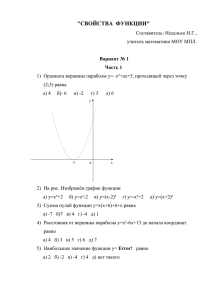
ЕН.Ф.3.Физика (новое окно)
реклама

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное автономное образовательное учреждение высшего профессионального образования «Дальневосточный федеральный университет» (ДВФУ) ФИЛИАЛ ДВФУ В Г. ПЕТРОПАВЛОВСК-КАМЧАТСКИЙ УЧЕБНО - МЕТОДИЧЕСКИЙ КОМПЛЕКС ДИСЦИПЛИНЫ Физика Специальность 140104.65 " Промышленная теплоэнергетика" Форма подготовки (очная/заочная) курс _1,2/2,3___семестр __2,3,4___ лекции __96/24__ (час.) практические занятия__78/12___час. лабораторные работы___60//20___час. всего часов аудиторной нагрузки____234/60____ (час.) самостоятельная работа ____316/490_____ (час.) контрольные работы (количество) _______/2 курсовой проект_________ экзамен____2,3,4_семестр/2,3 курс Учебно-методический комплекс составлен в соответствии с требованиями государственного образовательного стандарта высшего профессионального образования (209 тех/дс от 27.03.2000 г.). Учебно-методический комплекс дисциплины обсужден на заседании Методической комиссии ___ протокол № 9________от_____«01» __09__2011__г. Зам. председателя Методической комиссии ___________Т.И. Горева Составитель (ли):_____ к.ф.-м.н., профессор Кролевец А.Н._________________________ АННОТАЦИЯ Цель изучения дисциплины - обеспечение фундаментальной подготовки по физике, позволяющей будущим специалистам ориентироваться в научнотехнической информации, использовать физические принципы и законы, а также результаты физических открытий в практической деятельности в области промышленной теплоэнергетики. Изучение дисциплины должно способствовать формированию у студентов основ научного мышления, в том числе: пониманию гра-ниц применимости физических понятий и теорий; умению оценивать степень достоверности результатов теоретических и экспериментальных исследований; умению планировать физический и технический эксперимент и обрабатывать его результаты с использованием методов теории размерности, теории подобия и математической статистики. Изучение дисциплины на практических занятиях позволит студентам освоить методы постановки и выбора алгоритмов решения конкретных задач из различных областей физики. Студенты приобретут начальные навыки для самостоятельного овладения новыми методами и теориями, необходимыми в практической деятельности современного инженера. Студенты ознакомятся с техникой современного физического эксперимента, научатся использовать средства компьютерной техники при расчетах и обработке экспериментальных данных. На практических занятиях студенты закрепляют и конкретизируют полученные теоретические знания путем решения прикладных качественных и количественных задач, получают навыки моделирования процессов и явлений. Изучаемые в курсе «Физика» разделы являются базой для изучения теоретической механики, электротехники и электроники, технической термодинамики и термодинамического анализа циклов, тепломассообмена и др. 2 2. Начальные требования к освоению дисциплины Приступая к изучению физики, студент должен знать математику, химию, читать и конспектировать специальную литературу, иметь навыки работы с периодическими изданиями. 3. Требования к уровню освоения содержания дисциплины Студенты должны: знать: – наиболее общие свойства различных видов материи и форм их существования; – методы исследования, используемые в физике; – формулировки физических законов. уметь: – строить физические модели и решать конкретные задачи; – видеть естественно - научное содержание физических проблем, возникающих в практической деятельности специалиста. Студенты должны быть ознакомлены: – с противоречивостью развития физических гипотез и теорий; – с логической связью различных разделов физики; – с теоретическими методами физики. Студенты должны получить целостную систему знаний физики, формирующую физическую картину окружающего мира. 3 4. Объем дисциплины и виды учебной работы 4.1 Очная форма обучения Вид учебной работы Общая трудоемкость дисциплины Лекции (ЛК) Практические занятия (ПЗ) Лабораторные работы Контрольные работы (кол-во) Всего самостоятельная работа: Вид итогового контроля Всего часов 550 96 78 60 234 Семестр 2 Семестр 3 Семестр 4 34 16 16 28 28 28 - 34 34 16 - экзамен экзамен экзамен 4.2. Заочная форма обучения Вид учебной работы Общая трудоемкость дисциплины Лекции (ЛК) Практические занятия (ПЗ) Лабораторные работы Контрольные работы (кол-во) Всего самостоятельная работа: Вид итогового контроля Всего часов 550 24 12 20 2 490 Курс2 Курс 3 12 4 12 1 12 8 8 1 экзамен экзамен 4 5. Содержание дисциплины 5.1. Распределение учебного материала по видам занятий № п/п Раздел дисциплины Лек ПЗ ЛЗ СРС 2 2 10 10 10 4 2 4 6 6 6 4 14 14 16 10 34 16 16 54 7 7 7 7 28 7 7 7 7 28 7 7 7 7 28 22 24 22 22 90 6 6 10 6 24 4 10 10 6 6 6 4 34 96 16 60 4 2 34 78 14 16 20 20 90 234 2 СЕМЕСТР 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Введение Физические основы механики Элементы СТО Механика жидкостей и газов Физические основы молекулярной физики и термодинамики ИТОГО: 3 СЕМЕСТР Электростатика Постоянный электрический ток Электромагнетизм Электромагнитные колебания и волны ИТОГО: 4 СЕМЕСТР Оптика Взаимодействие электромагнитных волн с веществом Основы квантовой механики Квантовая статистика Зонная теория твердых тел Элементы атомной и ядерной физики ИТОГО: ВСЕГО: 5.2.Содержание лекционного курса Раздел 1 Физические основы механики 1..Место физики в системе наук о природе, эксперимент и теория в физических исследованиях. Физические модели. Пространство и время как формы существования движущейся материи. Физически основы механики. 2. Физические основы механики. Кинематика материальной точки. Понятие состояния в классической механике. Уравнения движения. Относительность движения. Системы отсчета. Координатная и векторная формы описания движения материальной точки. Перемещение, скорость, ускорение. Тангенциальное и нормальное ускорения. Кинематика движения по криволинейной траектории. Движение по окружности. Угловая скорость и угловое ускорения и их связь с линейными характеристиками движения. Кинематика материальной точки в движущейся системе координат. Преобразования Галилея. Классический закон сложения скоростей. 3.Динамика материальной точки. Взаимодействие материальных тел. Инерциальные и неинерциальные системы отсчета. Законы Ньютона. Масса. Сила.. Уравнения движения. Роль начальных условий. Принцип относительности Галилея. Фундаментальные взаимодействия в природе. Силы в классической механике. Закон всемирного тяготения. Свойства сил тяжести, упругости, трения. Движение материальной точки в неинерциальной системе отсчета. Силы инерции. Неинерциальность системы координат, связанной с Землей, ее проявления в геофизических явлениях. 5 4. Законы сохранения. Кинематика и динамика твердого тела. Понятие замкнутой системы. Импульс материальной точки, системы материальных точек. Законы сохранения. Центр масс системы материальных точек и закон его движения. Реактивное движение. Работа сил. Кинетическая энергия материальной точки. Потенциальные и не потенциальные силы в механике. Потенциальная энергия системы взаимодействующих тел. Момент импульса материальной точки и системы материальных точек. Момент силы. Движение твердого тела. Динамика вращательного движения твердого тела относительно неподвижной оси. Момент инерции твердых тел разной формы. Теорема Штейнера. Тензор инерции. Главные оси инерции. Уравнение моментов. Кинетическая энергия вращающегося тела. Плоское движение твердого тела. Раздел 2 Физика колебаний и волн 1. Колебания и волны .Колебательное движение. Уравнение свободных колебаний модельных систем (груз на пружине, математический и физический маятники). Гармонический и ангармонический осциллятор. Применение модели гармонического осциллятора к колебаниям молекул. Сложение колебаний. Затухающие колебания, их характеристики. Вынужденные колебания, явление резонанса. Понятие о колебаниях систем со многими степенями свободы. Нормальные колебания. Физический смысл спектрального разложения. 2.Волны в упругих средах. Кинематика волновых процессов. Волновое уравнение. Уравнение монохроматической бегущей волны, основные характеристики волн. Явление интерференции. Поток плотности энергии, связанный с бегущей волной. Стоячие волны. Явление дифракции волн. 3.Элементы гидро и аэродинамики жидкостей и газов. Движение идеальной жидкости, поле скоростей, линии и трубки тока. Уравнение Бернулли. Течение вязкой жидкости, формула Пуазейля. Ламинарные и турбулентные потоки. 4.Законы механики в движущихся системах отсчета. Основы релятивистской механики. Обобщенный принцип относительности. Основные постулаты специальной теории относительности Эйнштейна. Преобразование Лоренца. Раздел 3 Молекулярная физика и термодинамика 1.Молекулярная физика. Основные представления молекулярно-кинетической теории. Предмет и методы молекулярной физики. Статистический и термодинамический подходы. Случайные величины и их описание. Плотность вероятности. Средние значения, флуктуации. Термодинамические функции состояния. Равновесные состояния и процессы. Идеальный газ как модельная термодинамическая система. Основное уравнение молекулярно-кинетической теории идеального газа. Уравнение Клапейрона-Менделеева. Классическая и квантовая статистика. Распределение молекул идеального газа по скоростям (распределение Максвелла) и в поле потенциальных сил (распределение Больцмана). Барометрическая формула. Атмосфера Земли и других планет. Кинетические явления. Средняя длина свободного пробега. Явления переноса: диффузия, внутреннее трение и теплопроводность. 2. Термодинамики. Внутренняя энергия идеального газа. Термодинамические функции состояния. Работа термодинамической системы. Количество теплоты. Теплоемкость. Закон равнораспределения энергии по степеням свободы молекул. Три начала термодинамики. Обратимые и необратимые процессы. Циклические процессы. Цикл Карно. Коэффициент полезного действия тепловых машин. Энтропия и ее статистическая интерпретация. Возрастание энтропии при неравновесных процессах. Границы применимости второго закона термодинамики. Представление о термодинамике открытых систем. Фазовые равновесия и превращения. Конденсированное состояние. Порядок и беспорядок в природе. 3.Реальные газы. Силы молекулярного взаимодействия. Реальные газы. Уравнение Ван-дерВаальса. Переход из газообразного состояния в жидкое. Критические параметры. Эффект Джоуля-Томсона. Сжижение газов. 6 Раздел 4 Электричество и магнетизм 1. Электричество. Электростатика в вакууме и веществе. Электрический заряд. Закон Кулона. Напряженность электрического поля. Системы заряженных частиц. Принцип суперпозиции. Потенциал. Разность потенциалов. Диэлектрик в электрическом поле. Диполь. Дипольный момент. Вектор поляризации. Электростатическая теорема Гаусса. Вектор электрической индукции. Уравнение Пуассона. Условия на границе раздела двух сред. Проводник в электрическом поле. Распределение зарядов на проводнике. Электрическое поле внутри и вне проводника. Электростатическая защита. Электрическая емкость. Конденсаторы. Энергия электрического поля. Плотность энергии электростатического поля. 2.Постоянный электрический ток. Сила и плотность тока. Закон Ома для участка цепи и замкнутого контура. Сторонние силы. Электродвижущая сила. Закон Ома в дифференциальной форме. Разветвленные электрические цепи. Правила Кирхгофа. Работа и мощность электрического тока. Закон Джоуля-Ленца. Превращения энергии в электрических цепях. 3. Магнетизм. Магнитное поле. Магнитостатика в вакууме и веществе. Магнитное поле тока. Законы Био-Савара-Лапласа и Ампера. Сила Лоренца. Вектор магнитной индукции. Поток вектора магнитной индукции через замкнутую поверхность. Теорема о циркуляции вектора индукции магнитного поля. Магнитные свойства вещества. Молекулярные токи. Диа-, пара- и ферромагнетики. Вектор намагниченности. Магнитная восприимчивость и магнитная проницаемость. Представление о ядер-ном магнитном резонансе и электронном парамагнитном резонансе. Электромагнитная индукция. Закон Фарадея. Прави-ло Ленца. Индуктивность. Самоиндукция. Плотность энергии магнитного поля. Взаимоиндукция. Трансформатор. 4.Электропроводность твердых тел.Зависимость сопротивления металлов от температуры. Сверхпроводимость. Полупроводники. Эффект Холла. Электронная и дырочная проводимости, р-ппереходы. Диод, транзисторы, интегральные схемы. 5.Переменный электрический ток. Квазистационарные токи. Переходные процессы в цепях с емкостью и индуктивностью. Условие квазистационарности. Закон Ома для цепей переменного тока с омическим сопротивлением, емкостью и индуктивностью. Реактивное сопротивление. Колебательный контур. Свободные колебания. Собственная частота. Затухающие колебания. Вынужденные колебания. Явление электрического резонанса. 6.Связь электрического и магнитного полей. Обобщения теории Максвелла. Вихревое электрическое поле. Ток смещения. Уравнение непрерывности. Система уравнений Максвелла в интегральной и дифференциальной форме. Материальные уравнения. Электромагнитные волны. Волновое уравнение. Скорость распространения электромагнитных волн. Энергия и импульс электромагнитного поля. Теорема Пойнтинга. Шкала электромагнитных волн. Радиовещание, телевидение. Принцип относительности в электродинамике. Электромагнитное поле в движущейся системе координат. Релятивистские преобразования полей. Раздел 5 Оптика 1. Световые волны. Волновая оптика. Электромагнитная природа света. Оптический и видимый диапазоны электромагнитных волн. Волновое уравнение. Скорость света. Гармоническая волна. Плоские и сферические волны. Волновой фронт. Поляризация электромагнитных волн. Линейная, круговая, эллиптическая поляризации. Естественный свет. Энергетические и фотометрические характеристики светового потока. 2. Распространение света в изотропных средах. Дисперсия света. Электронная теория дисперсии. Нормальная и аномальная дисперсии. Линии поглощения. Закон Бугера. Отражение и преломление света на границе раздела диэлектриков. Формулы Френеля. Законы отражения и преломления. Поляризация света при отражении и преломлении. Угол Брюстера. Коэффициенты отражения и преломления света. Оптическое изображение. 3. Интерференция света. Интерференция монохроматических волн. Двулучевая интерференция. Суперпозиция плоских волн. Разность хода. Условия интерференционных максимумов и минимумов. Стоячие волны. Интерференция в тонких пленках. Полосы равной толщины и равного наклона. Просветление оптики. Интерференционные приборы. Бипризма. Билинза. Интерферометр Майкельсона. Применение интерференционных приборов. 7 4. Дифракция света. Принцип Гюйгенса-Френеля. Метод зон Френеля. Дифракция Френеля на круглом отверстии. Зонная пластинка. Пятно Пуассона. Дифракция Фраунгофера. Дифракция света на щели. Дифракционная расходимость. Гауссов пучок. Ближняя и дальняя зоны дифракции, приближение геометрической оптики. Дифракционная решетка. Дисперсионная область. Разрешающая способность. 5. Оптика анизотропных сред. Двойное лучепреломление в анизотропных кристаллах. Построение Гюйгенса. Поляризация света при двойном лучепреломлении. Поляризационные фильтры. Интерференция поляризованных волн. Прохождение света через кристаллическую пластинку. Поляризациионные приборы. 6. Генерация света. Квантовая оптика. Элементарная кванто-вая теория излучения света. Атом Бора. Спонтанное и вынужденное излучение. Лазеры. Инверсная населенность. Условия ген ерации. Принцип работы и конструкция лазера. Свойства лазерного излучения. Принцип голографии. 7. Рентгеновские лучи. Природа рентгеновских лучей. Сплошной спектр и характеристическое излучение. Дифракция рентгеновских лучей на кристаллической решетке. Формула Вульфа-Брегга. Раздел 6 Атомная и ядерная физика 1. Тепловое излучение. Законы Кирхгофа, Стефана-Больцмана, Вина. Формулы Рэлея- Джинса и Планка, квантовый характер излучения. Фотоны. 2. Взаимодействие фотонов с электронами. Внешний фото-эффект. Работы А.Г. Столетова. Уравнение Эйнштейна. Эффект Комптона. Давление света, опыт П.Н. Лебедева. 3. Теория атома по Бору. Спектры излучения и поглощения света для атомов и молекул. Опыты Резерфорда. Постулаты Бора. Опыт Франка и Герца. 4.Волновые свойства частиц. Опыт Девиссона и Джермера. Гипотеза де Бройля. Принцип неопределенности. Квантовая оптика. Квантовые состояния. Квантовые уравнения движения. Уравнение Шредингера. Корпускулярно-волновой дуализм в микромире. Фотоны. Волновая функция и ее статистическое толкование. Квантование энергии и момента импульса. Прохождение частиц через потенциальный барьер. Гармонический осциллятор в квантовой механике. Операторы физических величин. 5. Физика атомов. Строение атома. Магнетизм микрочастиц. Атомы водорода и щелочных металлов. Спин электрона. Магнитный момент атома. Эффект Зеемана. Квантовая статистика. Принцип Паули. Периодическая система элементов Д.И. Менделеева. Молекулярные спектры. Электроны в кристаллах. Взаимодействия атомов. Природа химической связи. Молекулы и кристаллы. 6. Атомное ядро. Состав ядра атома. Взаимодействие нуклонов в ядре. Ядерные силы и модели атомного ядра. Естественная и искусственная радиоактивность. Ядерные реакции, деление ядер. Цепные реакции. Использование ядерной энергии. 7. Элементарные частицы. Основные виды частиц, методы их регистрации. Систематика элементарных частиц. Типы взаимодействия. Кварки. 8. Эволюция Вселенной. Возраст Вселенной. Современная физическая картина мира. Иерархия структур материи. Теория расширения Вселенной. Основные представления и идеи общей теории относительности и ее следствия. Физическая картина мира как философская категория. 8 5.3. Содержание практических занятий № п/п часов 1 2 3 4 5 6 7 8 9 10 2 2 2 2 1 1 2 1 2 1 11 12 13 14 7 7 7 7 15 16 17 8 8 8 18 19 6 4 Наименование практических занятий 2 СЕМЕСТР Кинематика поступательного движения Кинематика вращательного движения Динамика поступательного движения Динамика вращательного движения Законы сохранения Специальная теория относительности Механика жидкостей и газов Уравнение состояния идеального газа Молекулярно-кинетическая теория Первое начало термодинамики 3 СЕМЕСТР Законы Кулона, напряженность электрического поля Работа, потенциал Проводники. Конденсаторы Постоянный ток. Законы Ома, правила Кирхгофа 4 СЕМЕСТР Постоянный ток. Мощность. Закон Джоуля – Ленца Магнитное поле в вакууме. Закон Био-Савара-Лапласа Магнитное поле в вакууме. Расчеты магнитных полей. Поток магнитной индукции Электрические колебания и волны. Уравнение волны Электрические колебания. Затухающие колебания в LCR контуре 9 5.4. Содержание лабораторных занятий № п/п номер раздела 1 2 3 4 5 2 2 2 2 4 6 7 8 4 4 5 9 10 5 5 11 6 12 7 13 14 7 7 15 16 17 18 19 20 8 8 9 9 10 10 21 10 22 23 24 10 10 10 25 26 27 11 14 15 Наименование лабораторной работы ( практического занятия ) 2 СЕМЕСТР Элементы теории ошибок физических измерений (2 часа) Изучение основного закона динамики на маятнике Обербека (4 часа) Нахождение момента инерции тела сложной формы (4 часа) Нахождение массы тела с переменным моментом инерции (4 часа) Определение коэффициента внутреннего трения жидкости методом Стокса (2 часа) 3 СЕМЕСТР Проверка уравнения неразрывности (4 часа) Определение расхода жидкости (4 часа) Изучение закона распределения Максвелла по скоростям для мельчайших частиц (4 часа) Изучение закона Джоуля – Томсона для реальных газов (4 часа) Определение отношений теплоемкостей воздуха методом Клемана и Дезорма (4 часа) Моделирование плоскопараллельного электростатического поля в проводящем листе (4 часа) Измерение сопротивления и определение удельного сопротивления проводника (4 часа) 4 СЕМЕСТР Измерение заряда и определение емкости конденсатора (2 час) Определение температурного коэффициента сопротивления проводника и ширины запрещенной зоны полупроводника. (2 часа) Изучение эффекта Холла в полупроводниках (2 часа) Исследование магнитного поля на оси цилиндрической катушки. ( 4часа) Вынужденные колебания и резонансы в электрических цепях (4 часа) Исследование затухающих колебаний в электрических цепях (2 часа) Определение радиуса кривизны линзы.(2 часа) Определение минимума и максимума интерференции с помощью колец Ньютона (2часа) Определение длины световой волны при помощи дифракционной решетки (2 часа) Определение периода дифракционной решетки (2часа) Проверка закона Малюса (2 часа) Изучение спектра ртутной лампы с измерением длины волны спектральных линий (2 часа) Изучение поляризации света (2 часа) Определение величины запрещенной зоны полупроводника (2часа) Изучение спектра водорода (2 часа) 6. Курсовое проектирование не предусмотрено. 10 7. Учебно-методическое обеспечение дисциплины 8.1 Основная литература 1. Т.И. Трофимова. Курс физики. М.: Изд. Высшая школа 2004 2. А.С.Кингсел, Г.Р.Локшин, О.А.Ольхов. Курс общей физики. М.: Изд. Физматлит 2004 3. А.АДетлаф, Б.М.Яварский. Курс общей физики. М.: Изд-во Высшая школа 2005 4. Зисман Г.А., Тодес О.М. Курс общей физики в 3-х т. М.: Изд. Наука 2003 5. Сивухин Д.В. Общий курс физики т.т. 1-5. М.: Изд. Наука 2005. 6. Иродов И.Е. Задачи по общей физике. М.: Изд. Наука – Физматлит 2004 7. Савельев И.В. Сборник вопросов и задач по общей физике. М.: Изд. Астрель 2004 8. Сабирова Ф.М Лекции по курсу общей физики. Квантовая физика: Учебно-методическое пособие http://window.edu.ru/resource/704/57704 9. Терлецкий И.А., Каменев О.Т. Физика. Часть 4. Атомная физика: Учебное пособие http://window.edu.ru/resource/124/45124 10. Лунин Л.С., Благин А.В., Баранник А.А Лекции по физике. Ч.1. Механика, молекулярная физика и термодинамика http://window.edu.ru/resource/757/61757 8.1.2 Дополнительная: 1. Акоста В., Кован К., Грэм Б. Основы современной физики. М.: Изд. Просвещение 2001 2. Матвеев А.Н. Электричество и магнетизм. М.: Изд. Высшая школа 2002 3. Матвеев А.Н. Оптика. М.: Изд. Высшая школа 2003 9. Контрольные задания и методические указания по изучению дисциплины 9.1 Методические указания для студентов очной формы обучения Студентам очной формы обучения предлагается в качестве формы самостоятельной работы выполнение следующих контрольных работ: Примеры контролирующих заданий к первой части курса физики Модуль 1 (Механика) 1. 2. 3. 4. 5. Вариант 1 Точка движется по окружности радиуса R = 2 м согласно уравнению = Аt3, где А = 2м/с3. В какой момент времени нормальное ускорение точки будет равно тангенциальному? Определить полное ускорение точки в этот момент времени. Шар массой m1 = 1.0 кг движется со скоростью V1 = 4.0 м/с и сталкивается с шаром массой m2 = 2.0 кг, движущемуся навстречу ему со скоростью V2 = 2.0 м/с. Найти скорости шаров после удара. Удар считать абсолютно упругим, прямым, центральным. Камень массы m бросили горизонтально с башни высотой h c начальной скоростью V0. Пренебрегая сопротивлением воздуха найти работу силы тяжести через t секунд после броска. Обруч и сплошной цилиндр, имеющие одинаковую массу m = 2.0 кг, катятся без скольжения с одинаковой скоростью V = 5.0 м/с. Найти кинетические энергии этих тел. На краю платформы в виде диска диаметром D = 2 м , вращающейся по инерции вокруг вертикальной оси с частотой n1 = 8 об/мин, стоит человек стоит человек массой m = 70 кг. Когда человек перешел в центр платформы, она стала вращаться с частотой n2 = 10 об/мин. 11 6. 7. 8. 9. Определить массу платформы. Момент инерции человека рассчитывать как для материальной точки. Имеется прямоугольный треугольник, у которого один катет 1 м, а угол между этим катетом и гипотенузой 30. Найти в системе отсчета, движущейся со скоростью 0.5 с вдоль другого катета длину гипотенузы. Мюоны, рождаясь в верхних слоях атмосферы, пролетают до распада 6 км при скорости 0.995 с. Определить время жизни мюона для наблюдателя на Земле. Какую скорость (в долях скорости света) нужно сообщить частице, чтобы ее кинетическая энергия равнялась удвоенному значению энергии покоя. Покоящаяся частица распалась на новую частицу массой m и на фотон с энергией .. Определить массу М распавшейся частицы. Модуль 2 (Молекулярная физика и термодинамика) 1. 2. 3. 4. 5. 6. 7. Вариант 1 Определить массу газа в баллоне емкостью 90 л при температуре 295 К и давлении 510 5 Па , если его плотность при нормальных условиях 1.3 кг/м3. Водород находится при температуре 30 К. Найти среднюю кинетическую энергию вращательного движения одной молекулы, а также суммарную кинетическую энергию всех молекул этого газа, количество вещества водорода 0.5 моль. 2 кг азота охлаждают при постоянном давлении от 400 до 300 К. Определить изменение внутренней энергии, работу и количество выделенной теплоты. Водород массой 40 г , имевший температуру 300 К , адиабатически расширился , увеличив объем в 3 раза. Затем при изотермическом сжатии объем газа уменьшился в 2 раза. Определить полную работу и конечную температуру газа. Тепловая машина с двумя молями двухатомного газа совершает цикл, состоящий из изохоры, изотермы и изобары. Максимальный объем газа в 3 раза больше минимального, изотермический процесс протекает при 450 К. Найти к.п.д. цикла и работу, совершаемую за цикл. Газ, являясь рабочим веществом в цикле Карно, получил от нагревателя теплоту 4.38 кДж и совершил работу 2.4 кДж. Определите температуру нагревателя, если температура охладителя 273 К. Найдите изменение энтропии и количество теплоты, переданное азоту массой 4 г, находящемуся при нормальных условиях. В результате изобарического расширения объем газа изменяется от 5 л до 9 л. Вопросы к экзамену по первой части курса физики: 1. Принцип относительности Галилея. Преобразования Галилея. Принцип относительности Эйнштейна. 2. Преобразования Лоренца Следствия из преобразований Лоренца (сокращение длины, замедление времени). 3. Инвариантные величины в релятивистской механике. Интервал. 4. Кинетическая энергия в релятивистском случае. Связь между релятивистским импульсом и полной энергией. 5. Сложение скоростей в теории относительности. 6. Основное уравнение динамики вращательного движения. 7. Момент инерции. Теорема Штейнера. 8. Момент импульса. Закон сохранения момента импульса. 12 9. Характеристики вращательного движения. Кинетическая энергия вращательного движения. 10. Распределение Максвелла. 11. Опытные законы идеального газа. 12. Основное уравнение молекулярно- кинетической теории идеальных газов. 13. Барометрическая формула. Распределение Больцмана. 14. Степени свободы. Закон равного распределения энергии по степеням свободы. 15. 1 начало термодинамики. Работа газа. Теплоемкости газа при постоянном объеме и постоянном давлении. 16. Адиабатический процесс, уравнения адиабаты. 17. Применение 1 начала термодинамики к изопроцессам. 18. 2 и 3 начала термодинамики. 19. Статистический и термодинамический смысл энтропии. Закон возрастания энтропии. 20. Тепловые двигатели и холодильные машины. К.п.д. цикла. Цикл Карно. Примеры контролирующих заданий ко второй части курса физики Модуль 3 (Электростатика и постоянный ток) 1. 2. 3. 4. 5. 6. 7. 8. 9. Вариант 1 В вершине равностороннего треугольника находятся одинаковые положительные заряды 2 нКл. Найти напряженность поля в середине одной из сторон. Сторона треугольника 10 см. Решение пояснить рисунком. Две параллельно расположенные плоскости заряжены разноименно: одна с поверхностной плотностью 0.4 10 –6 Кл /м2, а другая -0.6 10 –6 Кл /м2. Определить напряженность поля между плоскостями и за ними. Найти напряженность поля на оси тонкого кольца радиуса R, заряженного зарядом Q как функцию расстояния до центра кольца. Электростатическое поле создается шаром радиуса 1 м, равномерно заряженным с общим зарядом 50 нКл. Определить разность потенциалов для точек поля, лежащих на расстоянии 0.3 и 0.8 м от центра шара. Найти разность потенциалов между центрами тонких колец, радиуса R, заряженных зарядами +Q и – Q. Центры колец лежат на одной оси, расстояние между ними H. Найти зависимость напряженности и потенциала электрического поля, создаваемого бесконечным цилиндрическим диэлектрическим слоем с проницаемостью как функцию расстояния до оси цилиндров (в перпендикулярном оси направлении). Цилиндрический слой заряжен с объемной плотностью . Внешний и внутренний радиусы цилиндров a и b. В пространстве наполовину заполненном парафином ( =2 ) создано однородное электрическое поле, напряженность которого в воздухе Е1 =2 В/м. Вектор Е1 образует угол 60 с границей раздела парафин – воздух, которую можно считать плоской. Найти 1) вектор D в парафине, 2) поверхностную плотность связанных зарядов, 3) вектор Е2 в парафине. Плоский конденсатор с площадью пластин S заполнен двумя слоями диэлектрика с диэлектрическими проницаемостями 1 и 2 и толщинами l1 и l2 соответственно. Найти емкость конденсатора. Две концентрические сферы радиуса 20 см и 50 см заряжены одноименно с зарядом 100 нКл. Найти энергию электрического поля, локализованного между сферами. Модуль 4: (Электромагнетизм) Вариант 1 13 1. 2. 3. 4. 5. 6. 7. Круговой виток диаметром 200 мм намотан из 100 витков тонкого провода, по которому течет ток силой 50 мА. Найти индукцию магнитного поля в центре витка и на оси витка на расстоянии 10 см от центра. Коаксиальный кабель состоит из внутреннего и внешнего цилиндров с радиусами соответственно R1 и R2 . Вдоль поверхностей этих цилиндров в противоположных направлениях течет ток. Найдите магнитное поле Н на расстоянии r от оси кабеля в случаях, когда: а) R1 r R2 б) r R2 Изолированный провод диаметром (с изоляцией) 0,3 мм намотан так, что образует плоскую спираль из N = 100 витков. Радиус внешнего витка R = 30 мм. Каким магнитным моментом обладает эта спираль, когда по ней идет ток силы I = 10 мА? Чему равна в этом случае напряженность магнитного поля в центре спирали? Электрон и протон, удалённые друг от друга на значительное расстояние, находятся в однородном магнитном поле. Зная, что каждый из них движется по окружности, найти отношение их угловых скоростей. Масса протона в 1935 раз больше массы электрона. (Никакие силы, кроме силы Лоренца, на электрон и протон не действуют). В однородном магнитном поле с индукцией В = 0,84 Тл с небольшой скоростью вращается квадратная рамка со стороной а = 5 см, состоящая из небольшого числа витков медной проволоки сечением S = 0,5 мм2. Концы рамки соединены накоротко. Максимальное значение силы тока, индуцируемого в рамке при вращении, I = 1,9 А; а) определите число оборотов рамки в секунду; б) скажите, как нужно изменить скорость вращения рамки, чтобы при замене медной проволоки железной сила тока в цепи осталась неизменной. Модуль 5: Колебания и волны Вариант 1 1. Некоторая точка движется вдоль оси х по закону х = А sin2(t-/4). Найти: а) амплитуду и период колебаний; Изобразить график х(t); б) проекцию скорости vx как функцию координаты х; изобразить график vx(х). 2. Найти графически амплитуду А колебаний, которые возникают при сложении следующих колебаний одного направления: х1 = 3,0 cos(t + /3), х2 = 8,0 sin(t + /6); 3. В контуре, добротность которого Q = 50 и собственная частота колебаний 0 = 5,5 Гц, возбуждаются затухающие колебания. Через сколько времени энергия, запасенная в контуре, уменьшится в = 2,0 раза? 4. Амплитуды смещений вынужденных гармонических колебаний при частотах 1 = 400 с-1 и 2 = 600 с-1 равны между собой. Найти частоту , при которой амплитуда смещения максимальна. 5. К сети с действующим напряжением U = 100 В подключили катушку, индуктивное сопротивление которой XL = 30 Ом и импеданс Z = 50 Ом. Найти разность фаз между током и напряжением, а также тепловую мощность, выделяемую в катушке. 6. Плоская звуковая волна возбуждается источником колебаний частоты ,равной 100 Гц, амплитуда колебаний равна 4 мм. Скорость звуковой волны принять равной 400 м/с. Записать выражение (х, t), описывающее данную звуковую волну, если в начальный момент смещение точек источника максимально. 7. Определить разность фаз колебаний источника волн, находящегося в упругой среде, и точки этой среды, отстоящей на Х = 2 м от источника. Частота колебаний равна 5 Гц, скорость распространения волны 40 м/с. 14 Вопросы к экзамену по второй части курса физики (третий семестр обучения) 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30. 31. 32. 33. Электрический заряд. Его свойства. Закон Кулона. Электрическое поле. Напряженность электрического поля. Принцип суперпозиции. Теорема о циркуляции вектора E . Потенциал. Потенциал поля точечного заряда, системы зарядов. Свойства потенциала. Связь между потенциалом и вектором E . Поток вектора. Теорема Гаусса для вектора E . Расчет электростатического поля с помощью теорема Гаусса. Поле электрического диполя. Дипольный момент. Электрическое поле в диэлектриках. Типы диэлектриков. Поляризованность. Вектор электрического смещения D . Теорема Гаусса для вектора D . Связь между D, P и E . Диэлектрическая проницаемость. Граничные условия для E, D . Электрическое поле в проводниках. Напряженность электрического поля вблизи заряженного проводника. Потенциал проводника. Электроемкость. Конденсаторы. Энергия электрического поля. Э.Д.С., электрический ток, плотность тока. Законы Ома, Джоуля – Ленца в интегральной и дифференциальной формах. Взаимодействие движущихся зарядов. Магнитное поле. Вектор магнитной индукции – основная характеристика магнитного поля. Закон Био-Савара-Лапласа. Поле прямого тока. Поле в центре кругового тока. Закон полного тока (теорема о циркуляции вектора В) Поле прямого тока. Поле соленоида, тороида. Сила Лоренца. Движение электрического заряда в магнитном поле. Сила Ампера. Взаимодействие параллельных токов. Магнитный поток. Теорема Гаусса для магнитного поля. Работа по перемеще6ию проводников с током в магнитном поле. Явление электромагнитной индукции. Опыты Фарадея. Закон электромагнитной индукции. Правило Ленца. Индуктивность. Самоиндукция. Взаимная индукция. Принцип действия трансформатора. Теория Максвелла для электромагнитного поля. Вихревое электрическое поле. Ток смещения. Дифференциальное уравнение свободных незатухающих колебаний и его решения. Гармонический осциллятор. Пружинный маятник. Математический и физический маятники. Колебательный контур. Сложение гармонических колебаний. Метод векторных диаграмм. Разложение Фурье. Сложение колебаний одного направления: 1) с одинаковыми частотами; 2) с разными, но близкими частотами (биения). Сложение взаимно перпендикулярных колебаний с одинаковыми частотами. Дифференциальное уравнение затухающих колебаний и его решение. Характеристики затухания, коэффициент затухания, логарифмический декремент, добротность. Затухающие колебания пружинного маятника и колебательного контура. Дифференциальное уравнение вынужденных колебаний и его решение. Амплитуда установившихся вынужденных колебаний. Резонанс. Классификация и характеристики волн. Уравнение плоской волны. волновое уравнение. Фазовая скорость. Механические волны в упругих средах. Электромагнитные волны в вакууме. Главные свойства электромагнитных волн. Энергия электромагнитных волн. Вектор Умова-Пойнтинга. 15 34. Излучение электромагнитных волн. Излучение диполя. Излучение контура. Шкала ЭМВ. Примеры контролирующих заданий к третьей части курса физики Модули 6 и 7: («Оптика. Введение в квантовую механику, атомную физику и физику твердого тела») Примеры вариантов контрольной работы. Контрольная работа состоит из трех частей, которые проводятся 1 раз в месяц по мере прохождения материала. Часть 1 1. 2. 3. 4. 5. 6. Вариант 1 -частица движется по окружности радиусом 8.3мм в однородном магнитном поле, напряженность которого равна 18.9кА/м. Найти длину волны де Бройля -частицы. На щель шириной 20 мкм падает нормально параллельный пучок монохроматического света с длиной волны 500 нм. Найти ширину изображения щели (ширину главного максимума) на экране удаленном от щели на расстояние 1 м. Кинетическая энергия электрона в атоме водорода около 10эВ. Используя соотношение неопределенности оценить минимальные линейные размеры атома. Электрон находится в потенциальном ящике шириной 0.5нм. Определить наименьшую разность энергий энергетических уровней электрона. Принимая коэффициент черноты угля при температуре 600 К равным 0.8, определить энергию, излучаемую с поверхности угля площадью 5 см2 за время 10 мин. Постоянная дифракционной решетки в n = 4 раза больше длины световой волны монохроматического света, нормально падающего на ее поверхность. Определить угол между двумя первыми симметричными дифракционными максимумами. Часть 2 1. 2. 3. Вариант 1 Выразить среднюю скорость <v> электронов в металле при Т=0 К через максимальную скорость vmax . Вычислить <v> для металла, уровень ферми которого при 0 К равен 6 эВ. Имеется образец германия n-типа, легированного примесью с концентрацией 1015см-3. Концентрация собственных электронов зависит от температуры по закону ni2 3.110 32 T 3 exp 9100 / T , [см-6]. При температурах 100 К и 300 К найти: а) концентрацию электронов и дырок, б) положение уровня ферми, в) удельную проводимость. Считать, что при 100 К ионизировано 50% примеси, а при 300 К вся примесь, подвижности n=0.39 м2/(Вс), р=0.19 м2/(Вс). Пользуясь выражением для ВАХ идеального диода и определением температурного коэффициента тока (ТКI), TKI (1 / I (T0 )) (dI / dT ) T T , рассчитать ТКI для германиевого диода 0 4. (Еg=0.67эВ) при следующих условиях: прямое U=0.3В, Т=300К. Значение кТ/е=26мэВ при 300 К. Имеется образец полупроводника в виде кубика со сторонами 1см характеризующийся: n=1200 см2/(Вс), р=500 см2/(Вс), Na=1015см-3, Еа=0.05эВ, Nd=1015см-3, Еd=0.02эВ. К противоположным граням кубика приложено напряжение 1В. Нарисовать с соблюдением масштаба зависимость фототока, обусловленного примесями, от длины волны падающего на кубик излучения. 16 Часть 3 1. 2. 3. 4. Вариант 1 Для прекращения фотоэффекта в при облучении платиновой пластинки необходимо приложить задерживающую разность потенциалов 3.7 В. Если же вместо платиновой использовать другую пластинку, то под действием излучения с той же длиной волны максимальная энергия фотоэлектронов будет 6 эВ. Определит работу выхода из этой пластинки, если для платины она равна 6.3 эВ. Исходя из модели свободных электронов, определить число соударений, которое испытывает электрон за 1с, находясь в металле, если концентрация свободных электронов равна 10-29м-3. Удельная проводимость металла 10мсм/м. За какое время распадается четверть начального количества ядер радиоактивного изотопа, если период его полураспада 24 часа? Найти энергию ядерной реакции 147 N 01n146 C 11p , если энергия связи исходного ядра азота 104.66 МэВ, а энергия связи ядра углерода 105.29 МэВ. Пренебрегая кинетическими энергиями азота и нейтрона и считая их суммарный импульс равным нулю, найти также и кинетические энергии продуктов. Вопросы к экзамену по третьей части курса физики: (вопросы по содержанию 6 и 7 модулей, выносимые на аттестационный экзамен) 1. Оптика. Волновая природа света. Интерференция света. Способы получения когерентных волн. Расчет интерференционной картины от двух источников. Интерференция в тонких пленках Интерференция, дифракция. 2. Дифракция света. Принцип Гюйгенса – Френеля. Метод зон Френеля. Дифракция на малом отверстии и диске. Дифракционная решетка. 3. Поляризация света. Состояние поляризации. прохождение света через два поляроида. Закон Малюса. Дисперсия света. 4. Тепловое излучение. Характеристики и законы теплового излучения. 5. Волновые свойства вещества. Волны де Бройля. Соотношение неопределенностей. Волновая функция. Физический смысл квадрата модуля волновой функции. Уравнение Шредингера. 6. Электрон в потенциальной яме с бесконечно высокими стенками. Квантование энергии. 7. Туннельный эффект. 8. Атом водорода. Квантовые числа. Гиромагнитное отношение. Опыт Штерна-Герлаха. Спин электрона. Принцип Паули. Фермионы и бозоны. 9. Элементы зонной теории твердого тела. Диэлектрики, полупроводники, металлы. Динамика электрона в кристаллической решетке. Эффективная масса. 10. Функция распределения Ферми-Дирака. Уровень Ферми. Вырожденный и невырожденный электронный газ. Электронный газ в металлах. 11. Концентрация электронов и дырок в полупроводниках. 12. Зависимость электропроводности полупроводников и металлов от температуры. 13. Радиоактивность. Закон радиоактивного распада. 14. Строение ядра. Ядерные реакции. 17 10. Лабораторные занятия по дисциплине проводятся в лабораториях университета. Имеются лабораторные установки по механики, молекулярной физике, электричеству, магнетизму, оптики. Работы проводятся на стендах и установках, при этом на одной установке работает группа студентов в составе не более трех человек. 11. Текущий и итоговый контроль по дисциплине 11.1 Формы и методы текущего контроля Основными формами контроля текущей успеваемости студентов по дисциплине «Физика» являются: 1. Контрольная работа – индивидуальный контроль. 2. Экзамен – индивидуальный контроль. Основными методами текущей успеваемости студентов по дисциплине «Физика» являются: метод индивидуального контроля, метод устного и письменного контроля. 18 11.2 Перечень типовых экзаменационных вопросов 2 семестр Предмет механики. Представления Ньютона о свойствах пространства и времени. Системы отсчета. Понятие мате-риальной точки. Радиус - вектор. 2. Векторы перемещения , скорости. Проекции вектора ско-рости на координатные оси. 3. Вектор ускорения. Проекции вектора ускорения на коор-динатные оси. Тангенциальная и нормальная составля-ющие ускорения. 4. Траектория движения и пройденный путь. Вычисление пройденного пути. Принцип независимости движений. 5. Равномерное и равноускоренное прямолинейное дви- жение. 6. Движение точки по окружности. Угловое перемещение , угловая скорость , угловое ускорение. Связь линейных и угловых величин. Векторы угловой скорости и углового ускорения. 7. Первый закон Ньютона. Инерциальные системы отсче-та. Понятие о силе. Принцип независимости действия сил. Силы в природе. Фундаментальные взаимодейст-вия. 8. Второй закон Ньютона. Масса и ее измерение , аддитив-ность массы. 9. Импульс силы. Импульс тела. Закон сохранения импуль-са. 10. Принцип относительности Галилея. Третий закон Нью-тона. Границы применимости механики Ньютона. 1 1. Работа силы , мощность , энергия. 12. Связь силы с потенциальной энергией. Закон сохранения и превращения механической энергии. 13. Применение законов сохранения импульса и энергии к анализу упругого и неупругого соударений. 14. Система материальных точек. Силы внешние и внутрен-ние. Замкнутая система. Центр масс. Движение центра масс. Координаты центра масс. 15. Движение тела с переменной массой. 16. Энергия системы материальных точек. Консервативные и неконсервативные системы. Закон сохранения механи-ческой энергии в консервативной системе. 17. Твердое тело как система материальных точек. Абсолют-но твердое тело. 18. Поступательное и вращательное движение абсолютно твердого тела. 19. Момент силы. Момент силы относительно точки оси. Мо-мент пары сил. 20. Момент инерции. Теорема Штейнера. 21. Основное уравнение динамики вращательного движения твердого тела. 22. Кинетическая энергия твердого тела. Работа и мощность внешних сил при вращении твердого тела. 23. Момент импульса материальной точки. Момент импульса твердого тела. 24. Закон сохранения момента импульса твердого тела. 25. Условие равновесия твердого тела. Виды равновесия. Центр тяжести. 26. Неинерциальные системы отсчета. Силы инерции. Силы инерции в прямолинейно движущейся НИСО. 27. Равномерно вращающиеся НИСО. Центробежная сила инерции. 28. Сила Кориолиса. Проявления сил инерции на Земле. 29. Упругие свойства твердых тел. Виды упругих дефор-маций. Закон Гука. 30. Движение под действием упругих и квазиупругих сил. Колебательное движение. Гармонические колебания. Ам-плитуда , частота , фаза колебаний. 31. Смещение , скорость , ускорение при гармоническом ко-лебательном движении. Связь колебательного и враща-тельного движений , векторные диаграммы. 32. Сложение колебаний одного направления с одинаковыми и разными частотами. Биения. 33. Сложение взаимно перпендикулярных колебаний. Фигу-ры Лиссажу. 34. Математический и физический маятники. Кинетическая , потенциальная и полная энергия колеблющегося тела. 35. Затухающие колебания. 36. Вынужденные колебания. Резонанс. Волны. Распространение колебаний в однородной упругой среде. Продоль-ные и поперечные волны. Фазовая скорость волны. Урав-нение плоской гармонической бегущей волны. 37. Интерференция волн. Стоячие волны. 38. Всемирное тяготение. Закон тяготения Ньютона, постоян-ная тяготения и ее измерение. 1. 19 Гравитационная и инертная масса. 39. Напряженность и потенциал поля тяготения. 40. Первая , вторая и третья космические скорости. 41. Механика жидкостей и газов. Давления в жидкостях и газах. Измерение давления. Распространение давления в покоя-щихся жидкостях и газах. Закон Паскаля. Сила Архимеда. 42. Идеальная жидкость. Уравнение неразрывности струи. Уравнение Бернулли для идеальной жидкости и его след-ствие. Формула Торричелли. 43. Движение вязкой жидкости. Ламинарное и турбулентное течение. Число Рейнольдса. 44. Постулаты Эйнштейна. Одновременность событий. 45. Релятивистская кинематика. Собственное время. Преобра-зования Лоренца. 46. Релятивистское сокращение длин и сложение скоростей. Релятивистская динамика. 47. Импульс и энергия в специальной теории тносительности. 48. Статистический и термодинамический методы. Опытные законы идеального газа. 49. Молекулярные представления о веществе. Эксперимен-тальное обоснование молекулярнокинетической теории. 50. Идеальный газ. Основное уравнение молекулярно-кине-тической теории. 51. Температура. Абсолютная шкала температур. 52. Уравнение Клапейрона - Менделеева. 53. Внутренняя энергия. Распределение энергии по степеням свободы. 54. Распределение Максвелла. Распределение молекул по ско-ростям. 55. "Средние" скорости. Распределение молекул по энергиям. 56. Барометрическая формула. Распределение Больцмана. 57. Средняя длина свободного пробега. 58. Явления переноса в газах. Уравнение теплопроводности. 59. Явления переноса в газах. Уравнение диффузии. 60. Явления переноса в газах. Уравнение вязкости. 61. Количество теплоты. Теплоемкости Ср и Су. 62. Работа газа при расширении. 63. Первый закон термодинамики в применении к зопроцессам. 64. Адиабатический процесс. Уравнение адиабаты. 65. Работа в адиабатном процессе. Политропический про-цесс. 66. Обратимые и необратимые процессы. Круговые процессы. 67. Энтропия. Энтропия замкнутой системы. 68. Статистический смысл энтропии. 69. Второй закон термодинамики. Статистическая трактовка второго закона термодинамики. 70. Теорема Нернста. 71. Теорема Карно. Цикл Карно. КПД цикла Карно. 72. Холодильная машина. Холодильные коэффициенты. 73. Силы и потенциальная энергия межмолекулярного взаимодействия. 74. Уравнение Ван-дер-Ваальса. 75. Изотермы Ван-дер-Ваальса и их анализ. Изотермы реальных газов. 76. Внутренняя энергия реального газа. Адиабатическое рас-ширение газа в вакуум. 77. Эффект Джоуля-Томсона. Сжижение газов. 78. Свойства жидкостей. Поверхностное натяжение. 79. Смачивание. 80. Давление под искривленной поверхностью жидкости. 81. Капиллярные явления. 82. Насыщенный пар. 83. Твердые тела. Моно- и поли кристаллы. Анизотропия. Аморфные тела. 84. Закон Дюлонга и Пти. Зависимость теплоемкости твер-дых тел от температуры. 85. Фазовые переходы 1 и II рода. 86. Диаграммы фазового состояния. Тройная точка. 3 семестр 1. 2. 3. 4. 5. Электрический заряд. Взаимодействие электрических зарядов. Закон Кулона. Электростатическое поле. напряженность, линии напря-женности электростатического поля. Принцип суперпозиции. Поле диполя. Поток вектора напряженности. Теорема Гаусса. Напряженность поля бесконечной однородно заряжен-ной плоскости , двух плоскостей. 20 6. Напряженность поля бесконечного однородно заряжен-ного цилиндра. 7. Напряженность поля однородно заряженной сферы , шара. 8. Работа сил электростатического поля. 9. Циркуляция вектора напряженности электростатическо-го поля. 10. Потенциал электростатического поля. 11. Вычисление разности потенциалов по напряженности поля плоскости , двух плоскостей. 12. Вычисление разности потенциалов по напряженности по-ля сферы. 13. Вычисление разности потенциалов по напряженности поля шара. 14. Вычисление разности потенциалов по напряженности по-ля бесконечного цилиндра. 15. Связь напряженности поля и потенциала. Эквипотенци-альные поверхности. 16. Типы диэлектриков. Поляризация диэлектриков. 17. Описание электростатического поля в диэлектриках. Поляризованность. 18. Вектор электрического смещения. Теорема Гаусса для поля в диэлектрике. 19. Условия на границе разделов диэлектриков. 20. Проводники во внешнем электростатическом поле. Электрическая емкость. 21. Конденсаторы. Соединения конденсаторов. 22. Энергия системы зарядов. Энергия уединенного провод-ника. 23. Энергия заряженного конденсатора. Энергия электроста-тического поля. 24. Постоянный электрический ток. Сила тока. Плотность тока. 25. Сторонние силы. Электродвижущая сила. Напряжение. 26. Закон Ома для неоднородного участка цепи. Закон Ома для замкнутой цепи. 27. Закон Ома для однородного участка цепи. Соединения проводников. 28. Работа и мощность тока. Закон Джоуля - Ленца. КПД источника тока. 29. Правила Кирхгофа для разветвленных цепей. 30. Магнитное поле в вакууме. Опыт Эрстеда. Магнитная индукция. 31. Закон Био - Савара - Лапласа. 32. Магнитное поле прямого тока. Магнитное поле в центре кругового проводника с током. 33. Циркуляция вектора В магнитного поля в вакууме. 34. Магнитное поле соленоида. Магнитное поле тороида. 35. Закон Ампера. Взаимодействие параллельных токов. 36. Действие магнитного поля на движущийся заряд. 37. Эффект Холла. 38. Поток вектора магнитной индукции. Теорема Гаусса для магнитного поля. 39. Работа по перемещению проводника и контура с током в магнитном поле. 40. Электромагнитная индукция. ЭДС индукции. Токи Фуко. 41. Вращение рамки в магнитном поле. 42. Явление самоиндукции. Индуктивность. Индуктивность соленоида. 43. Экстратоки замыкания и размыкания. 44. Взаимная индукция. Коэффициент взаимной индукции. 45. Трансформаторы. 46. Магнитные моменты электронов и атомов. Диа и парамагнетизм. 47. Магнитное поле в веществе. Намагниченность. Закон полного тока. 48. Условия на границе раздела двух магнетиков. 49. Ферромагнетики и их свойства. 50. Энергия магнитного поля. 51. Основы теории Максвелла для электромагнитного поля. Ток смещения. 52. Система уравнений Максвелла в интегральной и диффе-ренциальной форме. 53. Гармонические электромагнитные колебания и их харак-теристики. 21 54. Затухающие электромагнитные колебания. Дифферен-циальное уравнение затухающих колебаний и его реше-ние. 55. Вынужденные электромагнитные колебания. Резонанс. 56. Квазистационарные токи. Переменный электрический ток. 57. Плоская электромагнитная волна. Уравнение бегущей волны. 58. Энергия электромагнитной волны. Вектор Умова-Пойнтинга. 59. Излучение диполя. 4 семестр 1. Развитие взглядов на природу света. Электромагнитная природа света. Световые волны. 2. Принцип Ферма. Оптическая длина пути. Законы отраже-ния и преломления. 3. Отражение и преломление плоской волны на границе двух диэлектриков. 4. Коэффициенты пропускания и отражения. 5. Геометрическая оптика- частный случай волновой. Зер-кала. Линзы. 6. Интерференция световых волн. Условия наблюдения ин-терференции. Двухлучевая интерференция. 7. Временная и пространственная и когерентность. Длина , радиус и объем когерентности. 8. Способы наблюдения интерференции. (Интерференцион-ные схемы. ) 9. Интерференция света в тонких пленках. Полосы равного наклона и равной толщины. 10. Кольца Ньютона. 11. Многолучевая интерференция. 12. Интерференционные приборы. Применение интерферен-ции. 13. Явление дифракции. Принцип Гюйгенса-Френеля. Зоны Френеля. Зонная пластинка. 14. Дифракция Френеля и Фраунгофера. Дифракция Френеля на круглом отверстии. 15. Дифракция Френеля и Фраунгофера. Дифракция Френеля на круглом экране. 16. Дифракция Френеля и Фраунгофера. Дифракция Френеля на краю полубесконечного экрана. 17. Дифракция Френеля и Фраунгофера. Дифракция Фраунго-фера на щели. 18. Дифракция Френеля и Фраунгофера. Дифракционная ре-шетка. 19. Угловая , линейная дисперсия и разрешающая сила диф-ракционной решетки. Критерий Рэлея. 20. Дифракция рентгеновских лучей. Формулы Лауэ. Форму-ла Вульфа-Брэгга. 21. Голография. Применение голографии. 22. Поляризованный свет и неполяризованный свет. Линей-ная, эллиптическая и круговая поляризация. 23. Способы получения поляризованного света. Степень по-ляризации. Закон Малюса. 24. Поляризация света при отражении и преломлении от диэ-лектрика. Закон Брюстера. 25. Поляризация света при двойном лучепреломлении. 26. Анализ поляризованного света. 27. Интерференция поляризованного света. Поляризационные приборы. 28. Искусственная анизотропия. Эффект Керра. Вращение плоскости поляризации. 29. Дисперсия света. Групповая и фазовая скорость волн. 30. Электронная теория нормальной дисперсии. 31. Поглощение света. Линейный коэффициент поглощения. Закон Бугера - Ламберта. 32. Рассеяние света. Закон Рэлея. 33. Эффект Вавилова - Черенкова. 34. Оптика движущихся сред. Способы определения скорос-ти света. Эффект Доплера. 35. Законы фотоэффекта. Объяснение фотоэффекта с класси-ческой и квантовой точек зрения. 36. Эффект Комптона. 37. Характеристики теплового излучения. Свойства равно-весного теплового излучения. Закон Кирхгофа. 38. Связь испускательной способности абсолютно черного тела с объемной плотностью равновесного теплового излучения в полости. 39. Квантование энергии излучения. Формула Планка. 40. Закон смещения Вина. Закон Стефана-Больцмана. 41. Устройство и принцип действия оптического пирометра. 42. Опыты по дифракции электронов : Дэвиссона и Джер-мера, Томпсона. 22 43. Соотношение неопределенностей Гейзенберга. 44. Гипотеза де Бройля. Корпускулярно-волновой дуализм. Волновая функция и ее физический смысл. 45. Уравнение Шредингера. 46. Частица в бесконечно глубокой потенциальной яме. 47. Квантовый линейный гармонический осциллятор. 48. Эффект туннелирования 49. Опыты Резерфорда. Планетарная модель атома. 50. Теория атома водорода по Бору. Историческая роль мо-дели атома Резерфорда - Бора. 51. Спектральные серии излучения атомарного водорода. 52. Квантово-механическая интерпретация постулатов Бора. Схема уровней энергии атома водорода. 53. Принцип соответствия Бора. 54. Опыты Франка и Герца. 55. Связь магнитного момента с моментом количества дви-жения. (Теорема Лармора). Магнетон Бора. 56. Опыты Штерна и Герлаха. Спин электрона. Пространст-венное квантование. 57. Полный набор квантовых чисел электрона в атоме. 58. Принцип Паули. Периодическая система элементов Д.И. Менделеева. 59. Природа характеристических рентгеновских спектров. Закон Мозли. 60. Химическая связь. Валентность. Образование молекул. 61. Условия поглощения или усиления света веществом. Устройство и принцип действия лазера. Свойства лазер-ного излучения. 62. Образование энергетических зон в кристаллах. 63. Классификация твердых тел. Металлы, диэлектрики, по- лупроводники. Энергия Ферми. Уровень Ферми в метал-лах. 64. Электроны и дырки в полупроводниках. Проводимость полупроводников. 65. Квантовая теория теплоемкости кристаллов. Теплоем-кость металлов. Фотоны. 66. Квантовые статистики. 67. Атомное ядро, его состав и характеристики. Изотопы. 68. Взаимодействие нуклонов. Понятие о ядерных силах. Несостоятельность протонноэлектронной теории ядра. 69. Протонно-нейтронная модель ядра. Энергия связи ядра. Дефект массы. 70. Ядерные и термоядерные реакции. 71. Элементарные частицы. ( систематика ) 72. Естественная радиоактивность. Физические основы ядер-ной и термоядерной энергетики. 73. Ускорители, методы получения и регистрации элементар-ных частиц. Посещаемость занятий учитывается поправочным коэффициентом, равным отношению количества часов посещенных занятий к плановым. 12. Тестовые задания по разделам курса I МЕХАНИКА ПРИНЯТЫЕ ОБОЗНАЧЕНИЯ Aа, а - работа rвектор и модуль ускорения, r12 - радиус – вектор вектор перемещения 23 линейный размер а, а - вектор и модуль тангенциального ускорения Еполная механическая энергия ех, единичные вектора в еy,еz, направлении осей x, y, z и еr радиус-вектора r gускорение свободного падения Iмомент инерции Ic момент инерции тела относительно оси, проходящей через центр масс kконстанта квазиупругой силы L, L - вектор и модуль момента импульса lдлина М, М mNР, р - вектор и модуль момента силы масса сила нормального давления вектор и модуль импульса R- радиус r- расстояние, смещение, s- путь Т- кинетическая энергия t- время UV,v - потенциальная энергия, вектор и модуль скорости vc - скорость центра масс x, y, z - координата, смещение , , , - вектор и модуль углового ускорения гравитационная постоянная коэффициент трения скольжения вектор и модуль угла поворота вектор и модуль угловой скорости ТЕСТОВЫЕ ЗАДАНИЯ 1. Что нужно поставить вместо многоточия в предложении: “Система отсчета, в которой тело ……., называется инерциальной.” а) движется с постоянным ускорением по отношению к другим системам отсчета; б) движется прямолинейно по отношению к другим системам отсче24 та; в) движется равномерно по отношению к другим системам отсчета; г) находится в состоянии покоя или равномерного прямолинейного движения. 2. Принцип относительности Галилея утверждает: а) все инерциальные системы отсчета по своим механическим свойствам эквивалентны друг другу; б) во всех инерциальных системах отсчета все законы механики записываются одинаковым образом; в) во всех инерциальных системах отсчета свойства пространства и времени одинаковы; г) все приведенные утверждения эквивалентны друг другу. 3. Радиус-вектор, определяющий положение материальной точки в пространстве, изменяется со временем по закону r = 3tex + 4tey + 7ez. Чему равен модуль скорости? а) 74 м/с; б) 25 м/с; в) 14 м/с; г) 8,6 м/с; д) 5 м/с. 4. Установите соответствие между потенциальной энергией тела в поле различных сил и ее математическим выражением. Математическое выражение Потенциальная энергия а) потенциальная энергия тела в поле консервативных сил 1) mgz б) потенциальная энергия тела в поле силы тяжести 2) Error! в) потенциальная энергия тела в поле упругой силы 3) Error! г) потенциальная энергия тела в гравитационном поле 4) Error!Fdr а) ; б) ; в) ; г) . 5. Момент инерции стержня длиной l относительно оси, проходящей через конец стержня, равен а) Error!; б) Error!; в) Error!; г) Error!; д) ml2. 6. Установите соответствие для моментов инерции однородных тел относительно оси zc, проходящей через центр масс тела. Твердое тело Ось zc Момент инерции 25 а) тонкий стержень длины a 1) ma2 б) сплошной цилиндр радиуса a 2) Error! в) тонкий диск радиуса a 3) Error! г) шар радиуса a 4) Error! д) обруч радиуса a 5) Error! а) ; б) в) ; г) ; ; д) . 7. Установите соответствие между силой и ее математическим выражением. Математическое выражение 1) F = N 2) F = rv 3) F = Error! Сила а) сила гравитационного взаимодействия б) сила тяжести в) сила упругости г) сила трения скольжения д) сила сопротивления 4) F = mg 5) F = kr а) ; б) ; в) ; г) ; д) . 8. Как изменится момент инерции двух материальных точек массами m, если ось OO перевести: (1) в положение I; (2) в положение II? I О m II m О а) увеличится, не изменится; в) увеличится, увеличится; д) увеличится, уменьшится; ж) уменьшится; не изменится; б) не изменится, увеличится; г) не изменится, не изменится; е) уменьшится; увеличится; з) не изменится; уменьшится. 26 9. Как изменится момент инерции свинцового цилиндра относительно оси, совпадающей с его геометрической осью симметрии, если цилиндр сплющить в диск? а) не изменится; б) увеличится; в) уменьшится. 10. Установите соответствие между физическим законом и его математическим выражением. Математическое выражение 1) Error!Ii i = const Закон а) второй закон Ньютона б) закон всемирного тяготения 2) E = T + U = const в) закон сохранения импульса 3) F = Error!er г) закон сохранения механической энергии 4) F = Error! 5) Error!miVi = const д) закон сохранения момента импульса а) ; б) ; в) ; г) ; д) . 11. В каком из приведенных ниже выражений допущена ошибка? а) V = r ; б) L = [r p]; в) M = [r F]; г) dr = [d r]; д) a = [ r]. 12. Какое из приведенных ниже выражений определяет перемещение материальной точки? г) r = Error! а) r12 = r2 – r1; б) r = xex + yey + zez; в) r = Vdt; Error!miri. 13. Какое из приведенных ниже выражений есть определение момента силы относительно точки? а) Error!; б) M = [r F]; в) M = I ; г) M = rF sin . 14. Какое из приведенных ниже выражений есть определение момента импульса относительно оси? а) L = [r P]; б) L = [r P] cos; в) L = I ; г) L = rpsin . 15. Кинетическая энергия твердого тела, вращающегося вокруг неподвижной оси, рассчитывается по выражению: а) Error!; б) Error!; в) Error!; г) Error! + Error! . 16. Кинетическая энергия твердого тела при сложном движении равна: 27 а) Error!; б) Error!; в) Error!; г) Error! + Error!; д) Error!. 17. При переходе из одной инерциальной системы отсчета K к другой - K', движущейся относительно первой со скоростью V0, в классической физике используется закон преобразования скорости: а) V' = V0 – V; б) V' = V + V0; в) V' = V – V0. 18. Проведите аналогию между величинами, характеризующими поступательное и вращательное движение. Поступательное движение а) r б) V в) a г) p д) F е) m Вращательное движение 1) I 2) L 3) 4)M 5) 6) а) ; б) ; в) ; г) ; 19. Условие равновесия твердого тела имеет вид: а) F =Error!Fi внеш = 0, M =Error!Mi внеш = 0; д) ; е) . б) M =Error!Mi внеш = в) F =Error!Fi внеш = 0, 0, L =Error!Li внеш = 0. L =Error!Li внеш = 0; 20. Работа внешних сил при повороте твердого тела вокруг неподвижной оси рассчитывается по выражению: а) A12 = Error! F dr; б) A12 = Error!F cos dr; в) A12 = Error! Fs ds; г) A12 = Error! M d. 21. Имеется система частиц, на которую не действуют внешние силы. В каких из приведенных ниже выражений законов сохранения допущены ошибки? 2) Error!Li = 1) E = T + U const; const; 3) Error!pi = const; 4) I const. а) 1, 4; в) 1, 3, 4; г) 3. б) 2; 22. Какое из приведенных ниже уравнений описывает равномерное прямолинейное движение? 1) v = v0 + at; 2) = 0 + t; а) 1; б) 2, 4; 3) v = Error!; в) 3; 4) = Error!; 5) s = v 0t + Error!. г) 3, 4; д) 5. 23. Какие из приведенных ниже уравнений описывают криволинейное ускоренное 28 движение? 2) = 0 + t; 1) v = v0 + at; а) 1, 2; б) 2, 5; 4) = Error!; 3) v = Error!; в) 3; 5) = 0t + Error!. г) 3, 4; д) 5. 24. В каком из приведенных ниже выражений допущена ошибка? 1) v = R; 2) a = R; 3) an = 2R; 4) s = R; 5) a = 2 + 4. а) 1; б) 2; в) 3; г) 4; д) 5. 25. Какому из графиков ускорения прямолинейного движения (рис. 1-4) соответствует график скорости (рис. 5)? x x x Vx x x а) 1; 1 5 4 2 3 б) 2; в) 3; г) 4. 26. Частица движется равномерно по траектории, изображенной на рисунке. В каких точках траектории ускорение частицы равно нулю? 5 4 3 а) 1, 5; б) 3; в) 1, 3 5; 2 1 г) 2, 4; д) 5. 27. Материальная точка движется равномерно по криволинейной траектории. В какой точке траектории ускорение максимально? 29 3 4 2 1 а) 1; б) 2; в) 3; г) 4. 28. Частица движется равномерно с постоянным по величине ускорением. Какова траектория движения частицы? а) прямая линия; б) кривая линия с перегибом; в) парабола; г) окружность. 29. Точка M движется равномерно по свертывающейся плоской спирали. Как изменяется модуль ускорения точки? M а) возрастает; б) не изменяется; в) уменьшается. 30. На рисунке изображены графики Vx(t) двух прямолинейных движений. Сравнить в этих движениях: а) модули ускорений а1 и а2; б) пути s1 и s2, пройденные точкой за время . Vx 1 2 1 2 а) а1 > а2, s1 > s2; г) а1 > а2, s1 < s2; ж) а1 > а2, s1 = s2; t б) а1< а2; s1 > s2; д) а1< а2; s1 < s2; з) а1< а2; s1 = s2; в) а1= а2; s1 > s2; е) а1= а2; s1 < s2; и) а1= а2; s1 = s2. 30 31. Как изменится угловое ускорение вала, если грузы переместить ближе к оси вращения? Момент сил, действующий на вал, сохраняется прежним. а) увеличится; б) уменьшится; в) не изменится. 32. Два диска с равными массами и радиусами R1 и R2 (R1 = 2R2) раскручивают из состояния покоя до одинаковых угловых скоростей. Найти отношение произведенных работ (A1 /A2 ). а) 1; б) 2; в) 4. 33. Происходит абсолютно неупругий удар частиц массами m1 = 4m2 и с кинетическими энергиями T2 = 6T1. Как движутся частицы после соударения? V1 V2 x m1 а) ; m2 б) ; в) частицы покоятся (v = 0). II ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ ПРИНЯТЫЕ ОБОЗНАЧЕНИЯ A- амплитуда колебания A0 - начальная амплитуда B- амплитуда колебания F0 - модуль вынуждающей силы 0 - амплитуда вынуждающей силы v x, y - скорость координата, смещение . x; . x; m .. x; - скорость амплитуда скорости ускорение 31 klmN- ускорение свободного падения константа квазиупругой силы длина масса число колебаний .. x; m 0 - rТt- коэффициент сопротивления период время 0 - g- амплитуда ускорения угол начальная фаза колебания коэффициент затухания логарифмический декремент затухания разность частот циклическая частота собственная частота колебания ТЕСТОВЫЕ ЗАДАНИЯ 1. Какое из приведенных ниже утверждений есть определение гармонического колебательного движения? а) движение, вызванное внешней периодически изменяющейся силой; б) движение, при котором периодически повторяются значения физических величин, определяющих это движение; в) движение, при котором смещение от положения равновесия со временем меняется по закону синуса или косинуса; г) движение, при котором все точки тела движутся по окружно32 стям с центрами, лежащими на одной прямой. 2. Зависимость координаты x от времени t имеет вид: 1) x = 4sin(t - /6); 2) x = А sin2t; 3) x = Аt sint; 4) x = А1 cos(t + ) + А2 cost; 5) x = А sin3t. Какие из зависимостей описывают гармонические колебания? а) 1; б) 2, 3; в) 1, 4; г) 3, 4; д) 5. 3. Какой из графиков, приведенных на рисунках, описывает зависимость от времени смещения точки от положения равновесия для гармонического колебательного движения? x x О О t t 2 1 x x О О t t 4 3 а) 1; б) 1, 2; в) 2, 3; г) 3, 4; д) 1, 4. 4. Задано уравнение гармонических колебаний: x=Acos(2πt/T + 0). Какое из нижеприведенных выражений представляет фазу этих колебаний? а) 2πt/T; в) 2π/T; б) 0; г) (2πt/T + 0); д) cos(2πt/T + 0). 5. Что называется амплитудой гармонических колебаний? a) смещение тела от положения равновесия в данный момент времени; б) расстояние между точками, колеблющимися в одинаковых фазах; в) расстояние между точками, колеблющимися в противоположных фазах; г) максимальное смещение тела от положения равновесия. 6. Написать уравнение гармонического колебания, если известны его параметры: амплитуда колебаний 5 см, циклическая частота 2π с–1, начальная фаза π/4. а) x = 5cos2π/Т(t + π/4); в) x = 5cos(2πt + π/4); б) x = 5cos2π(t + π/4); г) x = 5cos(2πt/T + π/4). 33 7. Уравнение колебаний имеет вид: x = Аsin(t + ). Какой из приведенных ниже графиков представляет зависимость скорости от времени, при условии, что = 0. а) 1; б) 2; в) 3; V V О V г) 4. О t t 1 2 V О О t t 3 4 8. Какова начальная фаза гармонического колебания x = Asin(0t + ), зависимость смещения которого от положения равновесия изображена на рисунке? x A0 О t а) 0; б) /2; в) /3; г) /6. 9. Колебательное движение описывается уравнением x = Acos(0t + ). Установите соответствие между энергией колебания и ее математическим выражением. а) кинетическая энергия колебаний Математическое выражение 1) Error! б) потенциальная энергия колебаний 2) Error! Энергия колебаний 3) Error! sin2(0t + ) в) полная энергия колебаний 4) Error! cos2(0t + ) г) средняя энергия колебаний а) ; б) ; в) ; г) . 10. Какие из приведенных зависимостей координаты x от времени t не описывают гармоническое колебательное движение? 1) x = Аsin(t – /6); 2) x = А1cos(t + ) + А2cost; 3) x = (2Аcos Error!t)cost; 4) x = А1cos1t + А2cos2t; 34 5) x = А0e–t·cos(t + ). а) 1; б) 2; в) 3; г) 4; д) 5. 11. Уравнение незатухающих колебаний имеет вид: x = Acos(0t + ). Приведите в соответствие закону изменения физической величины от времени математическое выражение. Математическое выражение 1) – A02 cos(0t + ) 2) – A0 sin(0t + ) 3) Acos(0t + ) 4) – m02 Acos(0t + ) Закон изменения а) силы б) смещения в) скорости г) ускорения а) ; б) в) ; г) ; . 12. Какое из приведенных ниже выражений определяет полную энергию затухающих колебаний? а) Error!; г) Error!. б) Error! e–2t; в) Error! e–t; 13. Что обозначает величина l в выражении периода колебаний физического маятника T = 2 Error!? a) расстояние от оси вращения до центра тяжести тела; б) приведенную длину физического маятника; в) расстояние от оси вращения до точки качания; г) расстояние между центром тяжести и точкой качания. 14. Из трех гармонических одинаково направленных колебаний с равными амплитудами и частотами, но различными начальными фазами: 1) 2/3, 2) 11/3; 3) 14/3; отобрать пары таких колебаний, которые при сложении гасят друг друга. а) 1 и 2; б) 1 и 3; в) 2 и 3. 15. При какой разности фаз: 1) /3, 2) /2, 3) , 4) /4 в результате сложения двух взаимно перпендикулярных колебаний с одинаковыми частотами получается линейное колебание. а) 1; б) 2; в) 3; г) 4. 16. Какова траектория движения точки, одновременно участвующей в двух взаимно перпендикулярных колебаниях вида: x = Аsint и y = Вcost. а) прямая линия; б) окружность; в) парабола; г) эллипс. 17. Из трех гармонических одинаково направленных колебаний с равными амплитудами и частотами, но различными начальными фазами: 35 1) /2, 2) 3/2; 3) 5/2 отобрать пары таких колебаний, которые при сложении дадут максимальную амплитуду. а) 1 и 2; б) 1 и 3; в) 2 и 3. 18. Установите соответствие между видом колебательного движения и уравнением, описывающим данный колебательный процесс. Колебательный процесс Уравнение а) свободные незатухающие колебания 1) x = А0e–t·cos(t + ) б) свободные затухающие колебания 2) x = Аcost, y = Вcost 3) x = Аcos(t + ) 4) x = Аcos Error! в) вынужденные колебания г) параметрические колебания а) ; б) ; в) ; г) . 19. Какое из приведенных ниже выражений дает значение логарифмического декремента затухания? а) k/m; б) r/2m; в) T; д) t. г) 2/; 20. Для рассматриваемых случаев установите соответствие между периодом и его математическим выражением. а) период колебания математического маятника Математическое выражение 1) T = Error! б) период колебания физического маятника 2) T = Error! в) период незатухающих колебаний 3) T = 2 Error! г) период затухающих колебаний 4) T = 2 Error! д) период биений 5) T = 2 Error! Период а) ; б) ; в) ; г) ; д) . 21. Приведите в соответствие колебательным процессам дифференциальные уравнения. Колебательный процесс а) незатухающие колебания б) затухающие колебания в) вынужденные колебания Дифференциальное уравнение .. . 1) mx; = – kx – rx; .. . 2) mx; = – kx – rx; + F0cost .. 3) mx; = – kx 36 а) б) ; в) ; . 22. Установите правильную последовательность в изменении периода Т для свободных колебаний, совершаемых в среде с коэффициентом затухания , равным: 1) = 0, 2) << 0, 3) = 0, 4) > 0. а) T1>T2> T3>T4; б) T1 T2>T3>T4; в) T1 T2<T3<T4; г) T1 T2<<T3T4. 23. Приведите в соответствие физические величины их математическим выражениям. Математическое Физическая величина выражение 1) Error! а) декремент затухания 2) Error! б) время релаксации 3) Error! в) добротность 4) T г) коэффициент сопротивления а) б) ; в) ; г) ; . 24. Установите соответствие между амплитудой и ее математическим выражением. Математическое выражение 1) A = Error! Амплитуда а) незатухающих колебаний б) затухающих колебаний 2) A0e–t., = 0 в) вынужденных колебаний 3) A0e–t., > 0 а) б) ; в) ; . 25. Какое из приведенных ниже выражений определяет резонансную амплитуду? а) Error!, б) Error!, в) Error!, г) Error!. 26. Какое из приведенных ниже выражений определяет резонансную частоту? а) 02 – 22; б) 02 – 2; в) Error!; г) Error!. 27. Уравнение гармонических колебаний имеет вид x = 5cos(πt/4 + π/2) cм. Чему равен период этого колебания? а) 0,25 с; б) π/4 c; в) 1/8 с; г) 4 с; д) 8 с. 28. Система выведена из положения равновесия и предоставлена самой себе. Какой будет вид зависимости x = (t) для случая > 0? 37 x x x t t t б) а) в) 29. Установите правильную последовательность в изменении для резонансных кривых, изображенных на рисунке. А 1 2 3 F0/k О а) 1 > 2 > 3; рез б) 1 > 2 < 3; 0 в) 1 < 2 > 3; г) 1 < 2 < 3. 30. Уравнение гармонических колебаний имеет вид x = 0,2cos5t м. Каково амплитудное значение скорости этого тела? а) 0,2 м/с; б) 0,5 м/с; в) 1 м/с; г) 50 м/с; д) 12 м/с. 31. Какую длину должен иметь математический маятник, чтобы период его колебаний был равен 2 с (g = 10 м/с )? а) 0,25 м; б) 0,5 м; в) 1 м; г) 2 м; д) 4 м. 32. Задано уравнение колебаний x=2e-0,1t sin(5πt + π/6) см. Чему равен логарифмический декремент затухания? а) 0,04; б) 0,1; в) 0,2; г) 0,5π; д) 10π. 33. На рисунке представлен график смещения x точки из положения равновесия в зависимости от времени t. Чему равен логарифм отношения амплитуд lnError! (где N – число полных колебаний). 38 х в) Error!; б) NT; А0 A2 A4 О A1 г) (T)N. A3 A5 t а) T; III МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА ПРИНЯТЫЕ ОБОЗНАЧЕНИЯ PQR- давление количество теплоты универсальная газовая постоянная S- энтропия, площадь D- работа, константа константа удельная теплоемкость при постоянном давлении и объеме молярная теплоемкость при постоянном давлении и объеме коэффициент диффузии Т- dFH- эффективный диаметр сила энтальпия tUu- hg- Vvвер - i- высота ускорение свободного падения число степеней свободы термодинамическая температура время внутренняя энергия скорость направленного движения объем наиболее вероятная скорость K- импульс kМ- постоянная Больцмана коэффициент теплопроводности молярная масса m- масса - NNА - число частиц постоянная Авогадро - Aac p , cv СP, СV - <v> vср. ар <v2> vср. кв x, y, z - средняя арифметическая скорость средняя квадратичная скорость координата, смещение отношение темплоемкостей Сp/СV коэффициент внутреннего трения вязкость средняя длина свободного пробега плотность эффективное сечение 39 n- концентрация, константа ТЕСТОВЫЕ ЗАДАНИЯ 1. Какие графики, изображенные на рисунках представляют изобарный процесс? Р Р 2 1 4 3 б) 3, 6, 8; 8 7 6 V а) 1, 5, 8; V 5 9 T T в) 2, 5, 7; г) 3, 6, 7; д) 2, 6, 9. 2. Какие процессы изображены на графиках? Как изменяется объем газа в процессе I (рис. 1) и давление газа в процессе II (рис. 2)? P V I Рис. 1. II T Рис. 2. T а) изобарический, V - увеличивается, P - уменьшается; б) изотермический, V – увеличивается, P - уменьшается; в) изохорический, V – уменьшается, P – увеличивается; д) изотермический, V – увеличивается, P – увеличивается. 3. Как изменяется с ростом температуры давление в газовом процессе, для которого ~ T –1? а) увеличивается; б) уменьшается; в) не изменяется. 40 4. В газовом процессе, для которого T2V = Const, P ~ Tn. Найти значение n. Масса газа постоянна. а) ½; б) 2; в) 3; г) – ½; д) – 2. 5. Чему равно общее число степеней свободы для молекулы идеального двухатомного газа? а) 2; б) 3; в) 4; г) 5; д) 6. 6. Сколько степеней свободы колебательного движения имеет молекула NH3? а) 3; б) 5; в) 6; г) 7; д) 9. 7. Объем некоторой массы идеального газа изобарически уменьшился в 2 раза. Как изменилась средняя энергия поступательного движения одной молекулы газа? а) увеличилась в 4 раза; б) уменьшилась в 4 раза; в) не изменилась; г) уменьшилась в 2 раза; д) увеличилась в 2 раза. 8. На рис. 1 в координатах P и V изображен процесс, проведенный с идеальным газом (m = сonst). Укажите номер графика, соответствующий этому процессу в координатах Р и Т на рис 2. P P a 4 3 2 b 1 b 3 a 1 b 5 b 0 а) 1; b 2 1 2 3 4 Рис. 1 б) 2; V Рис. 2 г) 4; в) 3; b 4 T д) 5. 9. Привести в соответствие графики, изображенные на рисунке, изопроцессам с идеальным газом? P 1 2 3 4 V Изопроцесс а) адиабатический График 1 41 б) изобарический в) изохорический г) изотермический 2 3 4 а) ; б) ; в) ; г) . 10. На рис.а в координатах P – V изображен круговой процесс с некоторым количеством идеального газа. Выберите из графиков, рассмотренных ниже, (рис. 1-4) график этого процесса в координатах P – Т. P b c a d V Рис. а P P c b c b d a a Рис. 1 T Рис. 2 P b d T P c c b a d d a T T Рис. 3 а) 1; б) 2; Рис. 4 в) 3; г) 4. 11. Установите соответствие между изопроцессом и выражением для работы расширения. Изопроцесс а) изотермический Математическое выражение 1) А = 0 2) А = Error! б) изобарический в) изохорический 3) А = P(V2 - V1) 4) А = Error! г) адиабатический а) ; б) ; в) г) ; . 12. Чему равно отношение CP/СV для идеального двухатомного газа при умеренных температурах? а) 1,01; б) 1,33; в) 1,40; г) 1,67; д) 1,80. 42 13. Установить правильную последовательность между отношениями = СP/CV для идеальных газов: 1) одноатомный, 2) двухатомный, 3) трехатомный. а) 1<2<3; б) 1<2>3; в) 1>2<3; г) 1>2>3. 14. Давление некоторой массы идеального газа изохорически уменьшилось в 2 раза. Как изменилась средняя энергия поступательного движения одной молекулы газа? а) увеличилась в 4 раза; б) уменьшилась в 4 раза; в) увеличилась в 2 раза; г) уменьшилась в 2 раза; д) не изменилась. 15. На рисунке изображен цикл из двух изобар и двух изохор. Пользуясь рисунком, выберите номера ответов, для которых приведены неправильные соотношения между температурами в состояниях 1, 2, 3, 4. P 1 2 4 3 V а) T4<T1<T2; г) T1>T4; T2>T3; б) T4<T3<T2; д) T4>T1>T2. в) T3>T4; T2>T1; 16. Изопроцессам поставьте в соответствие выражения первого начала термодинамики. Изопроцесс а) изотермический б) изобарический в) изохорический г) адиабатический а) ; б) Первое начало термодинамики 1) Q = dH 2) Q = A 3) А = – dU 4) Q = dU в) ; г) ; . 17. Два различных идеальных газа – одноатомный и двухатомный - находятся при одинаковой температуре и занимают одинаковый объем. Газы сжимаются адиабатически до уменьшения объема в 2 раза. Какой газ нагрелся больше? а) газы нагрелись одинаково; б) одноатомный нагрелся больше; в) двухатомный нагрелся больше. 18. Укажите среди нижеприведенных выражений то, которое соответствует энергии одной молекулы газа. а) Error!; б) Error! в) Error!; г) Error!; д) Error!. 43 ; 19. Найдите число степеней свободы молекул идеального газа, если 3/5 энергии его теплового движения приходится на поступательное движение молекул. а) 7; б) 3; в) 4; г) 5; д) 6. 20. Молярные теплоемкости гелия при процессах 1-2 и 2-3 (см. рис.) обозначены соответственно через С1 и С2. Найдите разность С1 и С2. P 1 2 3 V а) 2,5R; б) 2R; в) 1,5R; г) R; д) 0,5R. 21. Какое из приведенных выражений первого начала термодинамики применимо только к изотермическому процессу? а) Q = U + PV; г) Error!; б) U + A = 0; д) Error!. в) Q = U; 22. Установите соответствие между законом (определением) и его математическим выражением. Закон (определение) а) первый закон термодинамики б) второй закон термодинамики в) третий закон термодинамики г) определение энтропии д) объединенный закон Математическое выражение 1) Error! 2) S0 = 0 3) TdS = dU + PdV 4) dS = 0 5) Q = dU + PdV а) ; б) ; в) ; г) ; д) . 23. Поставьте в соответствие определениям их математические выражения. Определение а) уравнение состояния идеальных газов б) работа расширения в изотермическом процессе в) первый закон термодинамики г) внутренняя энергия идеального Математическое выражение 1) Error! 2) Error! 3) TV -1 = const 4) Error! 44 газа д) уравнение Пуассона а) ; б) 5) Q = dU + PdV в) ; г) ; ; д) . 24. На каких стадиях процесса, график которого дан на рисунке, газ поглощает теплоту? V III II I T а) I, II; б) II, III; в) I, III; г) I; д) II. 25. На графике изображены изотермы идеального газа (m = const). Как изменяются приращение внутренней энергии U и теплота Q при переходе от графика МА к графику МD? P М A В С D V1 V2 V а) U < 0, Q - уменьшается; б) U < 0, Q - возрастает; в) U > 0, Q - уменьшается; г) U > 0, Q - возрастает; д) U = 0, Q - уменьшается; е) U = 0, Q - возрастает. 26. Установить правильную последовательность в изменении температуры для схематически представленных на рисунке кривых распределения Максвелла Error! Т1 Т2 O Т3 v 45 по скоростям. а) T1 < T2 < T3; б) T1 < T2 > T3; в) T1 > T2 < T3; г) T1 > T2 > T3. 27. В каком соотношении находятся наиболее вероятная, средняя арифметическая и средняя квадратичная скорости: vвер : vср. ар : vср. кв? а) 1,22 : 1,13 : 1; г) 1 : 1,22 : 1,13; б) 1,22 : 1 : 1,13; д) 1,13 : 1,22 : 1. в) 1 : 1,13 : 1,22; 28. Сравнить средние квадратичные скорости молекул двух идеальных газов с параметрами Р1, 1 и Р2, 2, если Р1/Р2=2, a 2/1=1/2. а) v1 > v2; б) v1 < v2; в) v1 = v2. 29. Чему равно среднее значение <х2> некоторой величины х, функция распределения вероятностей значений которой изображена на рисунке. f(x) А -a а) Error!; O б) Error!; a x в) Error!; г) Error!; 30. Функции распределения частиц по квантовым состояниям поставьте в соответствие математическое выражение. Определение Математическое выражение 1) Ni = Error! а) распределение Гиббса 2) Ni = Error! б) распределение Больцмана в) распределение Ферми - Дирака 3) n = n0 e–mgh/kT 4) w = Error! г) распределение Бозе – Эйнштейна 5) Error! д) распределение Больцмана в гравитационном поле 46 а) ; б) в) ; г) ; д) ; . 31. Поставьте в соответствие закону (определению) его математическое выражение. Закон Математическое выражение а) сила внутреннего трения 1) Error! б) закон Фика (уравнение диффузии в газах) 2) Error! в) закон Фурье (уравнение теплопроводности в газах) 3) Error! г) уравнение вязкости в газах 4) Error! а) б) ; в) ; г) ; . 32. Установите соответствие между параметром и математическим выражением, вытекающим из молекулярно-кинетических представлений. Параметр Математическое выражение а) коэффициент теплопроводности 1) Error! б) коэффициент вязкости 2) Error! в) коэффициент диффузии 3) Error! г) средняя длина свободного пробега 4) 2d2<v>n д) среднее число столкновений 5) Error! а) ; б) ; в) г) ; ; д) . 33. На рисунке приведены нормированные зависимости давления молекул воздуха: а) H2, б) N2, в) O2, г), H2О, д) CO2 от высоты h над уровнем моря. Каждому из газов поставьте в соответствие кривую, описывающую зависимость давления от высоты. Р 1 2 3 4 5 h а) ; б) ; в) ; г) ; д) . 47 1. IV ЭЛЕКТРОСТАТИКА 2. ПРИНЯТЫЕ ОБОЗНАЧЕНИЯ Aработа Сэлектроемкость D, D - вектор и модуль электрического смещения dрасстояние E, Е - вектор и модуль напряженности электрического поля Еn нормальная составляющая вектора напряженности электрического поля UVW- напряжение объем энергия электрического поля Wp х- потенциальная энергия координата - угол 48 Еx F, F Fх ln- х-компонента вектора напряженности электрического поля единичные вектора в направлении осей x, y, z и радиус-вектора r вектор и модуль силы х-компонента вектора силы длина единичный вектор нормали Р- вектор поляризованности р, р q- вектор и модуль электрического момента электрический заряд qст - сторонний заряд q'изб R- избыточный связанный заряд радиус rS- радиус, расстояние поверхность, площадь ех, еy, еz, еr - - ЭДС, диэлектрическая проницаемость 0 = 8,8510–12 Ф/м (электрическая постоянная) Е - угол линейная плотность заряда объемная плотность заряда объемная плотность энергии электрического поля объемная плотность сторонст них зарядов избыточный объемносвязан'изб ный заряд поверхностная плотность заряда потенциал электрического поля 1 - 2 - разность потенциалов - диэлектрическая восприимчивость оператор набла ТЕСТОВЫЕ ЗАДАНИЯ 1. Какое из приведенных ниже выражений есть определение напряженности электрического поля? а) E = Error!; б) Е = Error!; г) S EdS = Error!Error! q i; д) E = Error!. в) E = Error!; 2. Установите соответствие между определением физической величины и его математическим выражением. Определение Математическое выражение 49 а) линейная плотность заряда 1) = Error! б) поверхностная плотность заряда 2) = Error! в) объемная плотность заряда 3) = Error! а) б) ; в) ; . 3. Напряженности электрического поля заряженного тела поставьте в соответствие математическое выражение. Напряженность электрического поля Математическое выражение а) точечного заряда на расстоянии r 1) E = Error! б) внутри объемно-заряженного шара в) бесконечно длинной равномерно заряженной нити на расстоянии r от ее оси г) бесконечной равномерно заряженной плоскости 2) E = Error! д) плоского конденсатора 5) E = Error! 3) E = Error! 4) E = Error! а) ; б) ; в) ; г) ; д) . 4. Как изменится по модулю напряженность электрического поля точечного заряда при уменьшении расстояния до заряда в 4 раза? а) уменьшится в 2 раза; б) уменьшится в 4 раза; в) уменьшится в 16 раз; г) увеличится в 2 раза; д) увеличится в 4 раза; е) увеличится в 16 раз. 5. Каково направление вектора напряженности электрического поля в точке О, созданного равными по модулю зарядами +q? +q 2 +q 3 +q О 4 1 +q a) 1; б) 2; в) 3; д) напряженность в точке О равна нулю. г) 4; 6. В каких из четырех случаев различного распределения зарядов, приведенных ниже, напряженность электростатического поля в точке А равна нулю? 50 A A –q +q +q A +q – + а) 1, 2; A Заряженное кольцо 1) 2) 3) б) 2, 3; в) 3; 4) г) 4; д) 3, 4. 7. Вблизи равномерно заряженной нити мысленно построим замкнутую поверхность, имеющую форму цилиндра, соосного с нитью I. Как изменится модуль потока вектора напряженности электрического поля через ту же поверхность цилиндра, если нить наклонить (II), сохранив пересечение нити с основаниями цилиндра? Среда однородна. I II а) увеличится; б) уменьшится; в) не изменится. 8. Установите соответствие между определением и его математическим выражением. Математическое выражение Определение 1) L Edl = 0 а) теорема Гаусса 2) S EdS = Error!Error!qi б) закон Кулона в) теорема о циркуляции 3) 2E2n = 1E1n г) поле диполя 4) Error! д) условие на границе двух однородных изотропных диэлектриков 5) E = Error! а) ; б) ; в) ; г) ; д) . 9. Укажите, на каком графике правильно показана зависимость напряженности электростатического поля Е от расстояния r для тонкой равномерно заряженной бесконечной нити r? 51 О r O О r а) О r б) r в) г) 10. Укажите, на каком графике правильно показана зависимость напряженности электростатического поля Е от расстояния r для равномерно заряженной проводящей сферы радиусом R. R r а) R r R б) r r R в) г) 11. Укажите, какие из нижеприведенных условий выполняются при равно-весии зарядов на проводнике? 2) = 0; 1) Eвн=const; а) 1, 2; б) 2; 4) = const. 3) Eвн = 0; в) 1, 3; г) 3, 4; д) 4. 12. Какой из приведенных ниже графиков отражает зависимость напряженности электростатического поля Е от расстояния r для равномерно заряженного по объему шара радиусом R? R r а) R б) r R в) r R r г) 13. Какое из приведенных ниже выражений есть определение потенциала электрического поля? а) = Error!; г) d = –Edr; б) = Error!; д) A = q(1 – 2). в) = Error!i; 14. Поставьте в соответствие потенциалу заряженного тела его математическое выражение. 52 Математическое выражение Потенциал 1) = Error! Error! а) потенциал точечного заряда Error! б) потенциал внутри заряженной сферы радиуса r в) потенциал системы точечных зарядов г) потенциал поля диполя д) потенциал тела с равномерно распределенным по объему зарядом а) ; б) в) ; 2) = Error! Error! 3) = const 4) = Error! Error! Error! 5) = Error! г) ; д) ; . 15. Какое из приведенных ниже выражений определяет энергию диполя в электрическом поле? г) W = Error! а) W = Error!; б) W = q; в) W = – pE cos; Error! qii. 16. При какой ориентации электрический диполь в однородном электрическом поле находится в положении устойчивого равновесия относительно поворотов? p p Е а) p Е Е в) б) 17. На рисунке показаны силовые линии и две эквипотенциальные поверхности 1 и 2 в электростатическом поле. Какие точки имеют одинаковые потенциалы? B C A а) А, В и С; б) B и С; D 2 1 в) А и D; г) B и D; д) С и D. 18. Какое из нижеприведенных выражений дает связь между напряженностью электростатического поля и потенциалом в неоднородном электрическом поле? а) Error!; г) Error!; б) Error!; д) Error!. в) Error!; 53 19. Укажите номера всех схем, на которых потенциал поля в центре правильного шестиугольника равен нулю. +q –q +q –q +q +q +q –q +q 1) +q +q +q –q –q +q +q –q +q 2) –q +q –q +q –q –q 3) 4) а) 1, 2, 3; б) 1, 4; в) 1, 3, 4; г) 2, 3, 4; д) 2,3. 20. Какой из нижеприведенных графиков качественно отражает зависимость потенциала от расстояния для уединенной металлической заряженной сферы радиуса R? R r R r R а) б) r r R в) г) 21. В каких из нижеприведенных случаев разность потенциалов между точками А и B равна нулю? B r A R Проводящий шар 1) а) 1, 5; B A + + A B A B B A q Проводящий шар 2) б) 2, 3; 3) 4) в) 2, 4; г) 2; 5) д) 4. 22. Указать ошибочную запись в выражениях, дающих работу А сил электростатического поля при перемещении заряда q из точки 1 в точку 2. 2 +q –q x 1 1) q(φ1-φ2) ; 2) Error! ; 3 3) Error! ; 54 4) Error! ; а) 1, 2, 3; 5) Error! . б) 2; в) 3; г) 3, 2; д) 4; е) 2, 5. 23. Силе электрического поля приведите в соответствие математическое выражение. Математическое выражение Сила электрического поля а) сила, действующая на заряд в электрическом поле б) сила, действующая на диполь в неоднородном электрическом поле в) сила притяжения меду пластинами плоского конденсатора 1) F = – Wp г) сила взаимодействия между точечными зарядами 4) Fx = p Error! cos д) сила электростатического поля 5) F = qE а) б) ; в) ; 2) F = Error! 3) Error! г) ; д) ; . 24. Какое из приведенных ниже выражений есть определение электроемкости конденсатора? а) C = 40R; г) С = Error!; б) С = Error!; в) С = Error!; д) С = Error!. 25. От каких факторов зависит емкость уединенного проводника, расположенного в вакууме? а) только от размеров проводника; б) только от формы проводника; в) от формы и размеров проводника; г) от формы, размеров и материала проводника; д) от формы, размеров и от заряда проводника. 26. Энергия заряженного проводника определяется выражением: а) Error!; б) Error!; в) Error!; г) Error!. 27. Энергия электрического поля определяется выражением: б) Error!; г) Error!. а) Error!; в) Error! ; 28. Электроемкости конденсатора поставьте в соответствие математическое выражение. Электроемкость Математическое вы55 ражение а) электроемкость плоского конденсатора 1) Error! б) электроемкость сферического конденсатора 2) Error! в) электроемкость цилиндрического конденсатора 3) Error! а) б) ; в) ; . 29. Какое из приведенных ниже выражений есть определение плотности энергии электрического поля? а) Error!; б) E = Error!; в) E = Error!; г) E = Error!. 30. Выберите из приведенных ниже выражений все те, которые определяют поток электростатического смещения D через поверхность S. 1) S DdS; а) 1, 2; 2) S Dcos(n,D)dS; б) 1, 3; 3) Error!; в) 2, 4; 4) S DdS; г) 3, 5; 5) Error!. д) 5. 31. Какое из приведенных ниже выражений есть определение электрического смещения? а) D = 0E; б) D = 0E + P; г) S DdS = Error!qi,ст; в) D = ст; д) D = Error!. 32. Какое из приведенных ниже выражений есть определение вектора поляризованности? а) P = 0E; г) P = Error! Error!pi; б) P = D - 0E; в) Р = – 'изб; д) S РdS = – q'изб. 33. На рисунке дано изображение электростатического поля на границе двух диэлектриков с диэлектрическими проницаемостями 1 и 2. Сравнить 1 и 2 между собой. Указать, линии какого поля Е или D изображены на рисунке. 1 2 а) 1>2, линии вектора Е; в) 1<2, линии вектора Е; б) 1>2, линии вектора D; г) 1<2, линии вектора D. 56 V ПОСТОЯННЫЙ ТОК ПРИНЯТЫЕ ОБОЗНАЧЕНИЯ работа, работа выхода электрона константа S - подвижность ионов константа вектор напряженности электрического поля вектор напряженности поля сторонних сил элементарный заряд =96484 Кл/г-экв число Фарадея tUu, u - АВ Е - l- сила тока вектор и модуль плотности тока постоянная Больцмана, постоянное число длина m- масса - n- объемная концентрация, постоянное число количество теплоты удельная теплота электрический заряд сопротивление внутреннее сопротивление источника - удельное сопротивление, объемная плотность заряда удельное сопротивление при температуре 0 К электропроводность (проводимость) коэффициент Томсона 1-2ПАВ ЭДС - коэффициентТомсона разность потенциалов коэффициент Пельтье электродвижущая сила оператор набла ABb СEE* eF- Ij, jk- QQqRr- Т- V,v А/Z - 0 - площадка, перпендикулярная к нормали поверхности термодинамическая температура время, температура напряжение вектор и модуль скорости направленного движения вектор и модуль скорости химический эквивалент температурный коэффициент сопротивления, степень диссоциации удельная термоЭДС ширина запрещенной зоны 57 площадь S - ТЕСТОВЫЕ ЗАДАНИЯ 1. Установите соответствие между материалом проводника и его электропроводностью. Электропроводность (, Ом–1см–1) 1) > 10–15 – 10–10 2) 10–10 – 103 3) 104 – 106 Материал а) металл б) полупроводник в) диэлектрик а) б) ; в) ; . 2. Проводящей среде поставьте в соответствие носители зарядов. Среда Носитель заряда 1) носители зарядов отсутствуют 2) электроны 3) ионы 4) ионы и электроны 5) электроны и дырки а) металл б) электролит в) полупроводник г) диэлектрик д) плазма а) ; б) в) ; г) ; ; д) . 3. Какое из приведенных выражений есть определение плотности тока? a) I Error!; = б) j Error!; = г) I = д) j = e+n+u+ + e–n–u–. Error!; в) I =Error! jdS; 4. Какое из приведенных ниже выражений определяет силу тока в проводнике? a) qvln/S, б) qvn, в) qvnS/l, г) qvnl, д) qvnS. 5. Проводящей среде поставьте в соответствие функциональную зависимость ее удельного сопротивления от температуры. Среда Функциональная зависимость 58 а) металл 1) = 0 eE/kT б) полупроводник 2) = 0 (1 + t) в) электролит 3) = Error! а) б) ; в) ; . 6. Какое из приведенных выражений определяет уравнение непрерывности для постоянного тока? a) S jdS = – Error! ; б) j = – Error!; в) j = 0; г) j = Const. 7. Интегральная форма закона Ома для неоднородного участка цепи выражается уравнением. a) I = Error!; б) I = Error!; в) I = Error!; г) j = E; д) j = (E + E*). 8. Установите соответствие между определением ЭДС и ее математическим выражением. Математическое выражение Определение ЭДС а) ЭДС - физическая величина, численно равная работе, совершаемой сторонними силами при перемещении положительного единичного заряда по замкнутой цепи б) ЭДС равна сумме падений напряжения на внешнем и внутреннем участках цепи в) ЭДС равна разности потенциалов на клеммах источника тока при разомкнутой внешней цепи г) ЭДС есть циркуляция вектора напряженности поля сторонних сил по замкнутому контуру а) ; б) ; в) 1) = L Edl 2) = Error! 3) = IR + Ir 4) = 1 – 2 ; г) . 9. Какое из приведенных ниже уравнений выражает дифференциальную форму закона Джоуля – Ленца? a) L jdS = – б) Q = IUt; в) Error!I2Rdt; г) Qуд = j. Error!; 59 10. Какое из приведенных ниже выражений определяет полную мощность тока в цепи? б) I (1 – 2); a) IU; в) I; г) I2R. 11. Поставьте в соответствие закону его математическое выражение. Математическое выражение 1) j = E 2) I = Error! Закон а) закон Ома для однородного участка цепи б) закон Ома в дифференциальной форме 3) I = Error! в) закон Ома для неоднородного участка цепи г) закон Ома для замкнутой цепи 4) j = nq(b+ + b–)E 5) I = Error! д) закон Ома для электролитов а) ; б) в) ; г) ; д) ; . 12. Поставьте в соответствие определению его математическое выражение. Математическое выражение 1) j = en0(u+ + u–)E 2) Ia = BUa3/2 3) Ik Rk = k Определение а) закон Джоуля – Ленца б) закон Ома для газов в) уравнение термоэлектронной эмиссии (формула Ричардсона – Дэшмана) г) формула Богуславского – Ленгмюра) k 4) Q = I 2Rt 5) j = CT 2exp(– Error! ) д) правило Кирхгофа а) ; б) в) ; г) ; k ; д) . 13. Сравните сопротивления двух проводников, для которых приведен график I = f(U). I 1 2 O U а) R1 > R2; б) R1 < R2; в) R1 = R2; г) по приведенным графикам о сопротивлениях 1 и 2 сказать ничего 60 нельзя. 14. На рис. 1-4 показаны четыре типа соединений трех одинаковых сопротивлений. Установите правильное соотношение общих сопротивлений этих участков. А В A B 1 2 А А B B 4 3 а) R1>R2<R3<R4; г) R1<R2<R3<R4; б) R1>R2<R3>R4; д) R1<R2<R3>R4; в) R1>R2>R3>R4; е) R1<R2>R3>R4. 15. На сколько равных частей нужно разрезать проволоку сопротивлением 48 Ом, чтобы при параллельном соединении этих частей получить сопротивление 3 Ом? а) 12; б) 4; в) 8; г) 16. 16. На схеме, изображенной на рисунке, R1 << R2 << R3. Определить приближенное значение сопротивления участка АВ? R2 R1 A а) R R1; б) R R2; R3 в) R R3; B г) не приведено верного ответа. 17. Имеется цепь из n равных последовательно соединенных сопротивлений. Как изменится сопротивление цепи, если их соединить параллельно? а) увеличится в n раз; в) уменьшится в n раз; б) увеличится в n2 раз; г) уменьшится в n2 раз. 18. При силе тока в цепи, равной I = kt2 (k – константа), за время t через сечение проводника переносится заряд q, равный: а) k; б) k t; в) k t 2/2; г) k t 3/3. 19. Как изменятся показания амперметра, если в цепи, схема которой показана на рисунке, замкнуть ключ? 61 A R R а) увеличится; в) уменьшится; R б) не изменится; г) определить нельзя. 20. Являются ли тождественными понятия: разность потенциалов и напряжение? а) да, являются; б) нет, не являются, но они совпадают для однородного участка цепи; в) нет, не являются и никогда не совпадают. 21. Максимальное количество независимых уравнений для электрической цепи, изображенной на рисунке, в соответствии с правилами Кирхгофа равно: а) 3; б) 5; в) 6; г) 4; д) 8. 22. Укажите, в каких уравнениях, составленных по правилам Кирхгофа для схемы, изображенной на рисунке, допущены ошибки? 2) I1R1 - I2(R2+r2) = 1 – 2; 4) I3R3 + I4R4 = 0. 1) I1 + I2 + I3 + I4 = 0; 3) I1(R1+r1) – I3R3 = 1; R5 r1 – + • A • r2 – + I5 R1 I1 R2 I2 R3 1, r1 • B – • A 2 r2 • – R1 + + I1 R2 • B I2 R3 I3 R4 I3 R4 I4 I4 62 а) 4; б) 2, 3; в) 3, 4; г) 1, 2. 23. Верны ли следующие утверждения: 1) при соединении двух проводников из различных металлов между ними возникает контактная разность потенциалов, которая зависит только от их химического состава и температуры; 2) разность потенциалов между концами цепи, состоящей из последовательно соединенных металлических проводников, находящихся при одинаковой температуре, не зависит от химического состава промежуточных проводников. а) верно, только 1; в) верны оба суждения; б) верно, только 2; г) оба суждения неверны. 24. Выберите из нижеприведенных явлений то, которое называется явлением Зеебека. а) явление возникновения тока в замкнутой цепи, составленной из двух разнородных металлов, спаи которых поддерживаются при различных температурах; б) явление возникновения разности температур на спаях двух разнородных металлов, образующих замкнутую цепь, по которой протекает ток; в) явление, сопровождающееся выделением (поглощением) тепла, дополнительного к Ленц-Джоулеву теплу, при прохождении тока по однородному проводнику, вдоль которого создан градиент температуры. 25. Изменится ли разность потенциалов двух разнородных металлов, приведенных в контакт, если между этими металлами поместить третий металл, отличный от первых двух? а) не изменится; б) увеличится; в) уменьшится; г) а priori сказать нельзя, все зависит от природы металла. 26. Каков физический смысл коэффициентов пропорциональности в выражении термоЭДС ε = α АВ (Т1 - Т2). а) численно равен термоЭДС, возникающей при разности температур спаев, равной (Т1 - Т2); б) численно равен отношению разности работ выхода электрона из металла двух разнородных металлов, составляющих термопару, к величине заряда электрона; в) численно равен величине термоЭДС, возникающей при разности температур спаев, равной одному градусу Кельвина. 27. Выберите все факторы, от которых зависит контактная разность потенциалов φ1 – φ2. 1) от химической природы контактирующих металлов; 63 2) от температуры контактирующих металлов; 3) от состояния поверхности; 4) от площади соприкосновения металлов. а) 1, 2; б) 1, 2, 3; в) 2, 3, 4; г) 3, 4, д) 1, 3, 4. 28. Закону (явлению) поставьте в соответствие математическое выражение. Математическое выражение 1) 1 – 2 = Error! lnError! Закон (явление) а) закон Фарадея а) + Error! б) закон Вольта 2) Q = ПАВIt в) явление Зеебека 3) dQ = I Error! dl г) явление Пельтье 4) = AB(T2 – T1) д) явление Томсона 5) m = Error! Error! It ; б) ; в) ; г) ; д) . 29. Функциональной зависимости поставьте в соответствие координаты и график. Функциональная зависимость Координаты Вид зависимости 64 а) вольт-амперная характеристика газового разряда ln О б) анодная характеристика лампы 1/Т E n г 4 j О д) зависимость удельного сопротивления электролита от концентрации в 3 О г) температурная зависимость электропроводности полупроводника б 2 j О в) температурная зависимость термоэмиссионного тока а 1 T д 5 I О U В ответе записывается цифра (координаты) и буква (вид зависимости). а) ; б) ; в) ; г) ; д) . 30. Функциональной зависимости поставьте в соответствие график. Функциональная зависимость Вид зависимости 65 а) температурная зависимость удельного сопротивления для металлов 1 О б) температурная зависимость удельного сопротивления для электролитов Т 2 О Т 3 в) температурная зависимость удельного сопротивления для сверхпроводников а) ; б) ; 0 О Т в) . 31. Какие из перечисленных ниже элементов при легировании германиевого полупроводника создают преимущественно электронную проводимость? а) B, Ga, As; б) In, P, Sb; в) P, Sb, As; г) B, In, Ga; д) Sb, As, Al. 32. Используя приведенные в следующем задании структурные элементы, постройте схему энергетических зон для а) чистого полупроводника, б) полупроводника с донорной примесью и в) полупроводника с акцепторной примесью (приведите последовательность энергетических зон по мере возрастания энергии). В ответе записывается последовательность структурных элементов (цифр). а) ; б) ; в) . 33. Используя приведенные ниже структурные элементы, постройте схему энергетических зон для: а) проводников, б) полупроводников и в) диэлектриков (приведите последовательность энергетических зон по мере возрастания энергии). 66 1 2 5 6 4 3 8 7 В ответе записывается последовательность структурных элементов (цифр). а) ; б) ; в) . 67