физика надо
реклама

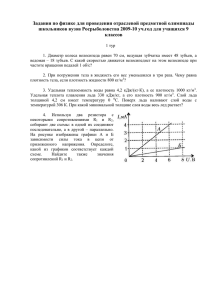
Задача 1. Если груз массы m = 10 г поставить на линейку на расстоянии x от её края, то линейка примет горизонтально с положение равновесия при размещении под ней упора на расстоянии y от того же края линейки (рис). Зависимость y(x) при различных размещениях груза представлена в таблице. Построив график зависимости y(x), X, мм У, мм определите массу линейки и ее длину. 10 120 Решение Рассмотрим систему в положение равновесия.Пусть длина.Запишем правило маментов отнсительно точки опоры: Mg(L/2-y)=mg(y-x) Преоброзовав ворожение получаем: m M y= x+ L m+M 2(m+M) 180 30 129 50 137 70 146 90 155 100 160 120 169 М-масса линейки,а L-ее 160 Посмороим график зависимости y от x. Из полученной формулы следует Что должна получиться прямая С угловым коэффициентом a=m /(M+m) пересекающая ось y в точке с кординатой yo=ML/(2m+2M) Определяем по графику Указанные параметры а=0,445,уо=115,3мм Из них получаем искомые характеристики линейки. 1-a М= m=12,5 г а 140 120 100 0 20 40 60 80 100 120 2yo =41,5 мм 1-a Ответ:Масса:12,5 г,Длина:41,5мм Задача 2. Силикатный кирпич имеет следующие размеры сторон: a = 5 см, b = 10 см и с = 20 см. Два таких кирпича поставили буквой T сначала на основание a × с (рис. а), а потом в аквариум, заполненный водой, на основание а × b (рис. б). В результате оказалось, что давление кирпичей на поверхность, одинаково. Найдите массу m такого кирпича. Поскольку кирпич шершавый, вода под него подтекает. Плотность воды ρ0 = 1000 кг/м3. L= ОТВЕТ: l = m/(ρπR2 ) ≈ 82 м Задача 3. Английский купец говорит русскому, что у них в Англии плотность золота 0,697 фунтов на дюйм в кубе. Русский купец отвечает, что если длину измерять в аршинах, а вес - в пудах, то плотность золота на Руси будет равна... Чему равна плотность золота на Руси? Примечание. В одном фунте 0,4536 кг, в одном футе 12 дюймов, в одном дюйме 25,4 мм, в 1 пуде 16,38 кг, в одной сажени три аршина или 2,1336 м. Решение Найдем переводнй коэффициент из фунтов в пуды 0,4536 а= = 27,7 . 10-3 16,38 Теперь из дюймов в аршины 25,4.10-3 B= = 35,71 . 10-3 1,1336/3 В одном куюическом дюймне содержится B3=(35,71.10-3)3=45,56 .10-6 Плотность золота равна a p=0,697 =424 пуда/аршин3 3 B Ответ:плоность :424 пуда/аршин3 Задача 4. Ко дну калориметра прикреплён плоский нагревательный элемент, над которым находится тонкий слой льда. После того, как нагревательный элемент включили на время τ1, лёд нагрелся па Δct = 2°С.. Какое время τ2, может потребоваться для увеличения температуры содержимого калориметра ещё на Δt = 2°С? Потерями теплоты в окружающую среду и теплоёмкостью калориметра можно пренебречь. Процесс теплообмена внутри калориметра можно считать достаточно быстрым. Удельная теплоёмкость льда с1 =2,1 кДж/(кг·°C), воды с2 = 4,2 кДж/(кг·°C), удельная теплота плавления льда λ = 330 кДж/кг. Решение После первого нагревания (в зависимости от конечной температуры льда) возможны следующие предельные варианты. 1. Если получился лёд при температуре меньшей или равной −2°C, то на повторный нагрев понадобится столько же теплоты и времени, сколько было затрачено на первый, а именно: Q=MC1Δt 2. Если получился лёд при температуре больше -2°C и меньше 0°C, тогда сначала придётся нагреть лед, затем его расплавить, а затем нагреть получившуюся воду. Так как теплоемкости воды и льда различны, то время нагрева на 2°C будет зависеть от температуры льда после первого нагревания. Очевидно, что крайние значение времени нагрева достигаются в случаях, когда температура льда после первого нагревания: а) чуть выше -2°C В этом случае необходимо затратить Q1 = mλ + mc1Δt теплоты. Подставляя значение m из (1), найдём Q1 = 79,6Q б) практически равна -0°C В этом случае необходимо затратить Q1 = mλ + mc2Δt теплоты. Подставляя значение m из (1), найдём Q2 = 80,6Q Искомое время нагревания равно τ1 или лежит в диапазоне 79,6τ1<τ2<80,6τ1 Ответ: 79,6τ1<τ2<80,6τ1 Задача 5. Пауки Stegodyphus раcificus, обитающие в Южной Азии, создают самую топкую в мире паутину. Ее диаметр 10 нм (1 нм = 10-9 м). Оцените длину паутины, которую мог бы сделать такой паук массой 0,2 г. Масса вещества, из которого образуется паутина, составляет 10% от массы наука. Плотность паука и паутины считайте приблизительно равными 10-3 кг/м3. Примечание. В физике понятие «оценить» означает, что вычисления следует делать приближенно. Например, оценим объем шара диаметром 3 см. Искомый объем немного меньше объёма куба со стороной 3 см. Объём куба равен 27 см3. Следовательно, оценочно, объём шара 10 см3. Задача 6. Турист первую треть всего времени движения шёл но грунтовой дороге со скоростью ν1 = 2 км/ч, затем треть всего пути перемещался по шоссе со Скоростью ν2. В конце второго участка пути он встретил грузовик, на котором и вернулся в исходную точку по той же дороге. Известно, что на грузовике он ехал с постоянной скоростью ν3. Вычислите среднюю (путевую) скорость ν0 туриста. Укажите минимальное возможное значение скорости ν2. Задача 7. Маугли принимал у удава Каа зачёт по развороту на 180о. Техника разворота такова: Каа, вытянувшись в линию, ползёт к Маугли со скоростью ν1,; как только голова удава касается ног мальчика, удав поворачивает ее на 180о и начинает выполнять разворот; при этом голова Каа удаляется от Маугли со скоростью ν2 > ν1, а хвост продолжает движение в прежнем направлении и с прежней скоростью (рис.). За какое время tо удав выполнит разворот? На каком расстоянии от ног мальчика окажется хвост удава сразу же после выполнения разворота? Считайте, что длина L удава Каа во время разворота не меняется. Задача 8. В боковой стенке бутылки проделано маленькое отверстие, в которое вставлена затычка. В бутылку начиняют воду и закрывают её горлышко пробкой, через которую пропущена трубка. Длина трубки подобрана таким образом, что её нижний конец находится выше отверстия в стенке бутылки, но ниже поверхности воды, а верхний конец сообщается с атмосферой. Затычку из отверстия в боковой стенке вынимают, и из него начинает вытекать вода. Через некоторое время поток воды из отверстия устанавливается, и вода вытекает с постоянной скоростью. Найдите давление воздуха P, находящегося в бутылке, в тот момент, когда нижний конец трубки находится на глубине h = 5 см от поверхности воды. Плотность воды ρ = 1000 кг/м3. атмосферное давление P0 = 100000 Па., ускорение свободного падения g = 9.8 м/с2. Задача 9. На горизонтальную поверхность льда при комнатной температуре T1 = 0 0С кладут копеечную монету, нагретую до температуры T2 = 50 °С.. Монета проплавляет лёд и опускается в образовавшуюся лунку. На какую часть своей толщины она погрузится в лёд? Удельная теплоёмкость материала монеты C = 380 Дж/(кг·°С), плотность его ρ = 8,9 гр./см3, удельная теплота плавления льда λ = 3,4·105 Дж/кг, плотность льда ρ0 = 0,9 гр./см3. Решение cm1(T2-T1)=qm2 - где c-уд.теплоемкость монеты, m1-масса монеты, q-уд.теплота плавления, m2-масса расплавленного льда; m1=p1V1=p1Sh1 - где p1-плотность монеты, S-площадь поверхности монеты=площадь лунки расплавленного льда, h1толщина монеты m2=p2V2=p2Sh2 - p2-где плотность льда, h2высота лунки распл.льда. следовательно cp1Sh1(T2-T1)=qp2Sh2 сократим на S: cp1h1(T2-T1)=qp2h2 тогда h1/h2 = qp2/cp1(T2-T1)=340000*900/380*8.9*(500-0)=181 Ответ:181 Задача 10. В люстре 6 одинаковых лампочек. Она управляется двумя выключателями, имеющими два положения «включено» и «выключено». От коробки с выключателями к люстре идут три провода. Лампочки в люстре либо: а) все не горят; б) все горят не в полный накал; в) три лампочки не горят, а три горят в полный накал. Нарисуйте возможные схемы электрической цепи.