Êàê óçðåòü ñâîé 34
реклама

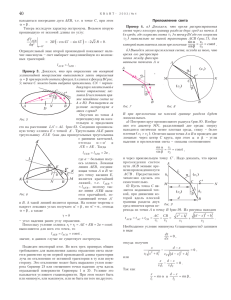
34 ÀÍT$ 2002/¹4 Ô È Ç È × Å ÑÊÊÂ È É ÔÀÊÓËÜÒÀÒÈ Êàê óçðåòü ñâîé çàòûëîê âäàëè À.ÑÒÀÑÅÍÊÎ ãäå c (R + Dr ) è n ( R + Dr ) = n ( R) + Dn ñêîðîñòü âîëíû è êîýôôèöèåíò ïðåëîìëåíèÿ íà âûñîòå Dr . Ïîñêîëüêó AA¢ = Rϕ , BB¢ = (R + Dr ) ϕ , èç âûðàæåíèÿ (1) ïîëó÷èì ...Âèäèøü, ñ êàêîé áûñòðîòîé âîñõîäÿùåå ñîëíöå âíåçàïíî Âñå îáëåêàåò êðóãîì ïîòîêàìè ÿðêîãî ñâåòà!.. Íî è òîò æàð, ÷òî èäåò îò ñîëíöà, è ñâåò åãî ÿñíûé Íå â ïóñòîòå ñîâåðøàþò ñâîé ïóòü; è äâèãàòüñÿ òèøå Ñâåò ïðèíóæäåí, ïîêà îí ðàññåêàåò âîçäóøíûå âîëíû... Ëóêðåöèé Î ×ÅÍÜ ËÅÃÊÎ ÍÀÁËÞÄÀÒÜ «ÏÐÅËÎÌËÅÍÈÅ» ×ÀÉ- íîé ëîæêè â ñòàêàíå âîäû. Åùå äðåâíèå ãðåêè ïûòàëèñü ïîëó÷èòü êîëè÷åñòâåííîå âûðàæåíèå çàêîíà ïðåëîìëåíèÿ.  ñëó÷àå ïðîçðà÷íûõ æèäêîñòåé ýòî ÿâëåíèå íàáëþäàåòñÿ ëåãêî, ïîñêîëüêó êîýôôèöèåíò ïðåëîìëåíèÿ n äëÿ íèõ çíà÷èòåëåí íàïðèìåð, ñêîðîñòü ñâåòà câ â âîäå â 4/3 ðàçà ìåíüøå, ÷åì ñêîðîñòü ñâåòà c â âàêóóìå: n = ñ ñâ = 4 3 .  ãàçàõ ýòîò êîýôôèöèåíò çíà÷èòåëüíî áëèæå ê åäèíèöå òàê, â âîçäóõå îí îòëè÷àåòñÿ îò åäèíèöû ãäå-òî â ÷åòâåðòîì çíàêå. Íî è ýòî îòëè÷èå âïîëíå îùóòèìî: çà ñ÷åò èñêðèâëåíèÿ ñîëíå÷íûõ ëó÷åé â àòìîñôåðå ìû âèäèì Ñîëíöå ðàíüøå åãî «ãåîìåòðè÷åñêîãî» âîñõîäà è ïîçäíåå çàõîäà (ñì. ðèñóíîê). Òàêèì îáðàçîì â ñóòêè íàáèðàåòñÿ äîïîëíèòåëüíî íåñêîëüêî «ëèøíèõ» ìèíóò ñâåòîâîãî äíÿ, à çà ãîä íåñêîëüêî ñóòîê, ÷òî íåìàëîâàæíî äëÿ êîëõîçíûõ ïîëåé è ëè÷íûõ îãîðîäîâ. Ýòî ÿâëåíèå íàçûâàåòñÿ àòìîñôåðíîé ðåôðàêöèåé. Åå ïðè÷èíà ïîíÿòíà: àòìîñôåðà ñ ïðèáëèæåíèåì ê Çåìëå ñòàíîâèòñÿ âñå ïëîòíåå, à ëó÷è îòêëîíÿþòñÿ â ñòîðîíó ñëîåâ ñ áóëüøèì êîýôôèöèåíòîì ïðåëîìëåíèÿ. À íåëüçÿ ëè âîîáðàçèòü ïëàíåòó ñ òàêîé àòìîñôåðîé, â êîòîðîé ëó÷ èñêðèâëÿåòñÿ íàñòîëüêî ñèëüíî, ÷òî âîçâðàùàåòñÿ â èñõîäíóþ òî÷êó? Òîãäà, â ïðèíöèïå, ìîæíî áûëî áû óâèäåòü ñâîþ ñïèíó âäàëåêå (ñì. ðèñóíîê á; ëó÷ OBB¢O ). Ïðàâäà, î÷åíü âäàëåêå, íà ðàññòîÿíèè ïîðÿäêà 2πR , ãäå R ðàäèóñ ïëàíåòû. Òàêîå ÿâëåíèå óìåñòíî íàçâàòü ñâåðõðåôðàêöèåé. ∆PH a P â á Çåìëÿ B¢ ∆r A¢ ϕ B A R Âåíåðà ( R + Dr ) ϕ (n ( R) + Dn) = Rϕn ( R) . Ðàñêðûâàÿ ñêîáêè è ïðåíåáðåãàÿ ìàëîé âåëè÷èíîé âòîðîãî ïîðÿäêà ( DrDn = 1 ), ïîëó÷èì ïðîñòîå óðàâíåíèå 1 Dn = . (2) nDr R Çíà÷èò, îòíîñèòåëüíàÿ óáûëü êîýôôèöèåíòà ïðåëîìëåíèÿ, îòíåñåííàÿ ê ïðèðàùåíèþ âûñîòû, äîëæíà áûòü ðàâíîé êðèâèçíå ïîâåðõíîñòè ïëàíåòû (îáðàòíîìó çíà÷åíèþ åå ðàäèóñà). Íî êàê êîýôôèöèåíò ïðåëîìëåíèÿ ñâÿçàí ñî ñâîéñòâàìè àòìîñôåðû? Ðàçóìíî ïðåäïîëîæèòü, ÷òî åãî îòëè÷èå îò åäèíèöû (ýòî çíà÷åíèå äëÿ âàêóóìà) ïðîïîðöèîíàëüíî êîíöåíòðàöèè N ìîëåêóë: n - 1 = αN , ãäå α íåêîòîðûé êîýôôèöèåíò. Ñëåäîâàòåëüíî, Dn αDN = » αDN (3) n n (òàê êàê ñàìî çíà÷åíèå n äëÿ ãàçîâ î÷åíü áëèçêî ê åäèíèöå). Ïîñêîëüêó ðàçìåðíîñòü êîíöåíòðàöèè ìîëåêóë [ N ] = ì-3 , êîýôôèöèåíò α äîëæåí èìåòü ðàçìåðíîñòü îáúåìà: [ α] = ì 3 . Îáúåìà ÷åãî? Íó êîíå÷íî æå, îí êàê-òî äîëæåí áûòü ñâÿçàí ñ îáúåìîì ìîëåêóë ãàçîâ, âõîäÿùèõ â ñîñòàâ àòìîñôåðû. Âîçüìåì Çåìëþ. Äëÿ âîçäóõà (èç ñîîòâåòñòâóþùèõ òàá-3 25 ëèö) αN » 3 × 10-4 , N = 2,7 × 10 ì ; çíà÷èò, α » 10-29 ì 3 . Äèàìåòð ìîëåêóëû àçîòà (îñíîâíîé êîìïîíåíò âîçäóõà) ðàâåí d » 3 × 10-10 ì , åå îáúåì ñîñòàâëÿåò - 3 4 æç d ÷ö 4 π × 27 × 10-30 3 ì » 4π × 10-30 ì3 : α . π çç ÷÷ = 3 è2 ø 3×8 Ñëåäîâàòåëüíî, ìîæíî ñ÷èòàòü, ÷òî ïðîèçâåäåíèå αN åñòü ñóììàðíàÿ äîëÿ îáúåìà, çàíÿòîãî («âûòåñíåííîãî») ñàìèìè ìîëåêóëàìè. À ÷òî òâîðèòñÿ, íàïðèìåð, íà Âåíåðå? Òàì èìååòñÿ ãîðÿ÷àÿ ( T » 800 Ê) è ïëîòíàÿ ( p » 100 àòì) àòìîñôåðà óãëåêèñëîãî ãàçà (åãî ìîëÿðíàÿ ìàññà ðàâíà 44 × 10-3 êã ìîëü ). Êîíöåíòðàöèÿ ìîëåêóë ó ïîâåðõíîñòè ðàâíà N= θ R Ñîëíöå O Äëÿ òîãî ÷òîáû ôðîíò âîëíû À ïîñëå ïîâîðîòà ðàäèóñàâåêòîðà íà óãîë ϕ îñòàëñÿ ïåðïåíäèêóëÿðíûì ïîâåðõíîñòè ïëàíåòû ( A¢B¢ ), íóæíî, ÷òîáû ó÷àñòêè ëó÷åé AA¢ è BB¢ ïðîõîäèëèñü âîëíîé çà îäíî è òî æå âðåìÿ: BB¢ AA¢ , t= = c ( R + Dr ) c ( R) èëè (1) BB¢ × n ( R + Dr ) = AA¢ × n ( R) , p 100 × 105 = ì-3 : 1027 ì-3 kT 1,4 × 10-23 × 800 (çäåñü k ïîñòîÿííàÿ Áîëüöìàíà). Ðàäèóñ ìîëåêóë óãëåêèñëîãî ãàçà â 1,25 ðàçà áîëüøå, ÷åì ó àçîòà; çíà÷èò, îáúåì áîëüøå ïî÷òè â äâà ðàçà, è α » 2 × 10-29 ì 3 . Èòàê, ó ïîâåðõíîñòè Âåíåðû èìååì αN » 0,02 , ÷òî íà äâà ïîðÿäêà áîëüøå, ÷åì äëÿ àòìîñôåðû Çåìëè. Äàëåå, èç óñëîâèÿ ðàâíîâåñèÿ ñòîëáà ãàçà âûñîòîé Dr è ñå÷åíèåì S: DpS = NmgDrS è èç âûðàæåíèÿ äëÿ äàâëåíèÿ ãàçà: p = NkT