Множество значений функции
реклама

"
ÊÂÀÍT 2007/¹4
Òåïåðü çàïèøåì óðàâíåíèÿ äèíàìèêè â ïðîåêöèè íà âåðòèêàëüíóþ îñü äëÿ äâèæåíèÿ òåëà ââåðõ è âíèç:
m
dvy
dt
= -kvy - mg , m
dvy
dt
= -kvy + mg .
Óìíîæèì íà ïðèðàùåíèå âðåìåíè è ïîëó÷èì äëÿ äâèæåíèÿ
ââåðõ è äëÿ äâèæåíèÿ âíèç, ñîîòâåòñòâåííî,
mdvy = -kdy - mgdt ,
mdvy = -kdy + mgdt .
Äëÿ âñåãî ïóòè çàïèøåì
-mvOy = -kH - mgt1 , mvAy = -kH + mgt2 .
Ñêëàäûâàÿ ýòè óðàâíåíèÿ ïîëó÷èì
-m∆v = -2kH + mgτ .
òèâëåíèÿ ñî ñòîðîíû æèäêîñòè ïðÿìî ïðîïîðöèîíàëüíà
ñêîðîñòè ïóçûðüêà), v0 = 1 ì ñ .
Ïðè ãîðèçîíòàëüíîì óñêîðåííîì äâèæåíèè òðóáêè íà
æèäêîñòü äåéñòâóþò ñèëû èíåðöèè, ñîçäàâàÿ «èñêóññòâåííóþ òÿæåñòü». Íà ýëåìåíò æèäêîñòè ìàññîé m äåéñòâóåò
r
ñèëà èíåðöèè -ma , íàïðàâëåííàÿ ïðîòèâ óñêîðåíèÿ. Ïîëå
ñèë èíåðöèè ñîçäàåò ñîñòàâëÿþùóþ àðõèìåäîâîé ñèëû,
íàïðàâëåííóþ ïî óñêîðåíèþ òðóáêè è ðàâíóþ
dv
FA = ρæVa = ρæV
.
dt
Ýòî ïðèâåäåò ïóçûðåê â äâèæåíèå. Èç-çà ïðåíåáðåæèìîé
ìàññû ïóçûðüêà ìîæíî çàïèñàòü
ur
ur
dv
= kv .
FA + Fc = 0 , èëè ρæV
dt
Óìíîæèì íà dt è ïîëó÷èì ïðîïîðöèîíàëüíîñòü äèôôåðåíöèàëîâ:
ρæVdv = kdx .
Îòñþäà íàéäåì èñêîìóþ âåëè÷èíó:
H=
m ∆v + g τ ∆L0 ∆v + g τ
=
.
2
2
k
vAx
Çàäà÷à 9*.  ñåðåäèíå äëèííîé öèëèíäðè÷åñêîé òðóáêè ñ
ãëèöåðèíîì íàõîäèòñÿ âîçäóøíûé ïóçûðåê. Ïðè âåðòèêàëüíîì ïîëîæåíèè òðóáêè ïóçûðåê ïîäíèìàåòñÿ ñî ñêîðîñòüþ 1 ì/ñ. Òðóáêó ðàñïîëîæèëè ãîðèçîíòàëüíî è ðàçîãíàëè âäîëü äëèííîé ñòîðîíû äî ñêîðîñòè 20 ì/ñ. Ãäå îñòàíîâèòñÿ ïóçûðåê? Êóäà îí ñìåñòèòñÿ, åñëè ñêîðîñòü ïëàâíî
óâåëè÷èòü äî 30 ì/ñ?
Ðàññìîòðèì ñíà÷àëà âåðòèêàëüíûé ïîäúåì ïóçûðüêà. Äëÿ
óñòàíîâèâøåãîñÿ ðåæèìà ïðè óñëîâèè ìàëîñòè ìàññû ïóçûðüêà àðõèìåäîâà ñèëà êîìïåíñèðóåòñÿ ñèëîé ñîïðîòèâëåíèÿ ãëèöåðèíà:
ur
ur
FA + Fc = 0 , èëè ρæVg = kv0 ,
Ñóììèðóÿ è óòî÷íÿÿ êîíå÷íûå ïðèðàùåíèÿ, äëÿ ïåðâîãî
ñëó÷àÿ, êîãäà òðóáêó ðàçãîíÿþò äî ñêîðîñòè v1 = 20 ì ñ ,
çàïèøåì
ρæV
v1 = x1 .
k
Ñ ó÷åòîì óðàâíåíèÿ äëÿ âåðòèêàëüíîãî ïîäúåìà ïóçûðüêà
íàéäåì
vv
x1 = 0 1 = 2 ì .
g
Àíàëîãè÷íî, äëÿ âòîðîãî ñëó÷àÿ, êîãäà ñêîðîñòü òðóáêè
óâåëè÷èâàþò äî v2 = 30 ì ñ , ïîëó÷èì
x2 =
v0v2
= 3 ì.
g
ãäå ρæ ïëîòíîñòü æèäêîñòè (ãëèöåðèíà), k êîýôôèöèåíò
ïðîïîðöèîíàëüíîñòè ìåæäó ñèëîé ñîïðîòèâëåíèÿ è ñêîðîñòüþ (áóäåì ñ÷èòàòü, ÷òî ïðè äàííûõ ñêîðîñòÿõ ñèëà ñîïðî-
Âèäíî, ÷òî ñìåùåíèå ïóçûðüêà ïðîïîðöèîíàëüíî ñêîðîñòè
òðóáêè.
Çàìå÷àíèå. Ðåøèòå ñàìîñòîÿòåëüíî ýòó çàäà÷ó áåç èñïîëüçîâàíèÿ ñèëû èíåðöèè.
Ìíîæåñòâî
çíà÷åíèé
ôóíêöèè
Öåëü ýòîé ñòàòüè ïðåäñòàâèòü ðàçëè÷íûå ìåòîäû íàõîæäåíèÿ ìíîæåñòâà çíà÷åíèé ôóíêöèè. Äëÿ äåìîíñòðàöèè
ýôôåêòèâíîñòè ðàññìàòðèâàåìûõ ìåòîäîâ íåêîòîðûå çàäà÷è
è óïðàæíåíèÿ ïîâòîðÿþòñÿ â ñòàòüå íåñêîëüêî ðàç. Íîìåðà
òàêèõ çàäà÷ è óïðàæíåíèé ñîõðàíÿþòñÿ.
Íà÷íåì ñ íåñëîæíûõ ïðèìåðîâ.
Çàäà÷à 1. Íàéäèòå ìíîæåñòâî çíà÷åíèé ôóíêöèè
y = sin x + cos x .
Ðåøåíèå. Âîñïîëüçóåìñÿ ñïîñîáîì ââåäåíèÿ âñïîìîãàòåëüíîãî óãëà:
Ñ.ËÀÂÐÅÍÎÂ
×
ÀÑÒÎ, ÐÅØÀß ÇÀÄÀ×È, ÀÁÈÒÓÐÈÅÍÒ (ÈËÈ ØÊÎËÜÍÈÊ,
ñäàþùèé ÅÃÝ) ñòàëêèâàåòñÿ ñ íåîáõîäèìîñòüþ îòûñêàíèÿ îáëàñòè çíà÷åíèé òîé èëè èíîé ôóíêöèè. Íàïîìíèì, ÷òî
åñëè íà íåêîòîðîì ìíîæåñòâå D [ f ] Ì R çàäàíà ôóíêöèÿ
y = f ( x ) , y Î R , òî ìíîæåñòâîì çíà÷åíèé E [ f ] ýòîé ôóíêöèè íàçûâàåòñÿ ìíîæåñòâî âñåõ òàêèõ y Î R , ÷òî y = f ( x )
ïðè íåêîòîðîì x Î D [ f ] .
1
æ 1
ö
sin x +
cos x ÷ =
y = 2ç
è 2
ø
2
πö
æ
2 sin ç x + ÷ .
è
4ø
Îòâåò: éë - 2; 2 ùû .
Çàäà÷à 2. Íàéäèòå ìíîæåñòâî çíà÷åíèé ôóíêöèè
πö
æ
y = cos2 x + 2 sin ç 2x - ÷ .
è
4ø
Ðåøåíèå. Ïðåîáðàçóÿ äàííîå âûðàæåíèå è ââîäÿ âñïîìîãàòåëüíûé óãîë ϕ , ïîëó÷èì
y=
1
1
1
5
+ sin 2x - cos 2x = +
sin (2x - ϕ) .
2
2
2
2
ÏÐÀÊÒÈÊÓÌ
é1 - 5 1 + 5 ù
Îòâåò: ê
;
ú.
2 û
ë 2
Óïðàæíåíèå 1. Íàéäèòå âñå çíà÷åíèÿ à, ïðè êîòîðûõ ìíîæåñòâî çíà÷åíèé ôóíêöèè y = ax 2 + x + 1 âêëþ÷àåò îòðåçîê [ -1; 1] .
Ðàçðåøèìîñòü óðàâíåíèÿ f ( x ) = a
Îòûñêàíèå ìíîæåñòâà çíà÷åíèé ôóíêöèè òåñíî ñâÿçàíî ñ
ðåøåíèåì óðàâíåíèé.
Òåîðåìà 1. Óðàâíåíèå f ( x ) = a èìååò ðåøåíèå òîãäà è
òîëüêî òîãäà, êîãäà à ïðèíàäëåæèò îáëàñòè çíà÷åíèé
ôóíêöèè y = f ( x ) .
Äîêàçàòåëüñòâî ñëåäóåò íåïîñðåäñòâåííî èç îïðåäåëåíèÿ
ìíîæåñòâà E [ f ] .
Èç òåîðåìû 1 ñëåäóåò, ÷òî äëÿ îòûñêàíèÿ E [ f ] äîñòàòî÷íî
íàéòè âñå çíà÷åíèÿ à, äëÿ êîòîðûõ óðàâíåíèå f ( x ) = a èìååò
êîðåíü x Î [ f ] . Ìíîæåñòâî òàêèõ à è ÿâëÿåòñÿ ìíîæåñòâîì
E [f ] .
Çàäà÷à 3. Íàéäèòå ìíîæåñòâî çíà÷åíèé ôóíêöèè
y = 15 + 2x - x 2 .
Ðåøåíèå. Âûÿñíèì, ïðè êàêèõ çíà÷åíèÿõ à óðàâíåíèå
15 + 2x - x 2 = a èìååò ðåøåíèå. Óðàâíåíèå ýêâèâàëåíòíî
ñèñòåìå
2
2
ïì15 + 2x - x = a ,
í
ïîa ³ 0.
Óðàâíåíèå ñèñòåìû èìååò ðåøåíèå ïðè D 4 = 16 - a2 ³ 0 ,
ïîýòîìó 0 £ a £ 4 .
Îòâåò: [0; 4] .
Èíîãäà àáèòóðèåíòû ïðèñîåäèíÿþò ê ñèñòåìå íåðàâåíñòâî
15 + 2 x - x 2 ³ 0 . Îäíàêî ýòîãî äåëàòü íå íóæíî, òàê êàê îíî
âûòåêàåò èç ïåðâîãî óðàâíåíèÿ ñèñòåìû.
Çàäà÷à 4. Íàéäèòå ìíîæåñòâî çíà÷åíèé ôóíêöèè
3 cos x + 1
y=
.
3 + sin x
3 cos x + 1
= a ðàâíîñèëüíî óðàâÐåøåíèå. Óðàâíåíèå
3 + sin x
íåíèþ 3 cos x - a sin x = 3a - 1 , ò.å.
cos ( x + ϕ) =
3a - 1
3 + a2
,
ðàçðåøèìîìó òîãäà è òîëüêî òîãäà, êîãäà
(3a - 1)2
3+a
2
£ 1 , ò.å. ïðè a Î [ - 1 4; 1] .
Îòâåò: [ - 1 4; 1] .
Çàìå÷àíèå. Ìû âîñïîëüçîâàëèñü ââåäåíèåì âñïîìîãàòåëüíîãî óãëà. ßâíî ðàçðåøàòü óðàâíåíèå îòíîñèòåëüíî õ ìû íå
ñòàëè, òàê êàê ýòîãî îò íàñ íå òðåáîâàëîñü. Äîñòàòî÷íî
îïðåäåëèòü óñëîâèÿ ñóùåñòâîâàíèÿ ðåøåíèÿ, ÷òî è áûëî
ñäåëàíî.
Óïðàæíåíèÿ
Íàéäèòå ìíîæåñòâî çíà÷åíèé ôóíêöèè:
2. y =
x 2 - 3x + 1
.
x2 + 1
2 - cos x
.
3. y =
4 + 3 sin x
"!
ÀÁÈÒÓÐÈÅÍÒÀ
Ðàññìîòðåííûé ìåòîä ïðèìåíèì è äëÿ ôóíêöèé íåñêîëüêèõ ïåðåìåííûõ, íà êîòîðûå íàëîæåíû äîïîëíèòåëüíûå
îãðàíè÷åíèÿ. Ðàññìîòðèì äëÿ îïðåäåëåííîñòè ôóíêöèþ äâóõ
ïåðåìåííûõ. Ïîñòàíîâêà çàäà÷è îáû÷íî òàêîâà: íàéòè ìíîæåñòâî çíà÷åíèé ôóíêöèè z = f ( x, y ) ïðè îãðàíè÷åíèè
g ( x, y ) = 0 (èëè g ( x, y ) £ 0 ).  òàêèõ çàäà÷àõ òðåáóåòñÿ
íàéòè çíà÷åíèÿ ïàðàìåòðà à, ïðè êîòîðûõ èìååò ðåøåíèå
ñèñòåìà
ìï f ( x, y ) = a,
í
ïî g ( x, y ) = 0.
Çàäà÷à 5. ×èñëà õ è ó óäîâëåòâîðÿþò ðàâåíñòâó
7x2 - 4xy + 4y2 = 12 . Íàéäèòå âñå çíà÷åíèÿ, êîòîðûå ìîæåò ïðèíèìàòü ñóììà x 2 + y2 .
Ðåøåíèå. Íàéäåì âñå çíà÷åíèÿ à, ïðè êîòîðûõ èìååò
ðåøåíèå ñèñòåìà óðàâíåíèé
ìï x2 + y2 = a,
í 2
2
ïî7 x - 4 xy + 4 y = 12.
Óìíîæèì ïåðâîå óðàâíåíèå íà 12, âòîðîå íà à è âû÷òåì îäíî
èç äðóãîãî. Ïîëó÷èì ýêâèâàëåíòíóþ ñèñòåìó
ìï(7a - 12) x2 - 4axy + (4a - 12) y2 = 0,
í 2
2
ïî7x - 4xy + 4y = 12.
Åñëè ó = 0, òî ïîëó÷èì à = 12/7, x = ± 12 7 . Ïóñòü y ¹ 0 .
Ïîäåëèì ïåðâîå óðàâíåíèå íà y2 è ïîëîæèì t = x/y. Òîãäà
(7a - 12) t2 - 4at + 4a - 12 = 0 . Ïðè à = 12/7 êîýôôèöèåíò
ïåðåä t 2 îáðàùàåòñÿ â 0, íî ïðè ýòîì çíà÷åíèè ñèñòåìà
èìååò ðåøåíèå. Åñëè a ¹ 12 7 , òî óðàâíåíèå èìååò ðåøåíèå, åñëè D 4 = -24a2 + 132a - 144 ³ 0 . Îòñþäà a Î [3 2; 4] .
Ïðè ýòîì 12 7 Î [3 2; 4] . Èòàê, x = ty ïðè íàéäåííûõ à.
Ïîäñòàâëÿÿ ýòî âûðàæåíèå âî âòîðîå óðàâíåíèå, ïîëó÷èì
y2 7t2 - 4t + 4 = 12 . Êâàäðàòíûé òðåõ÷ëåí, ñòîÿùèé â ñêîáêàõ, ïîëîæèòåëåí, ïîýòîìó ñóùåñòâóåò ó, à ñëåäîâàòåëüíî,
ñóùåñòâóåò è õ.
Îòâåò: [3 2; 4] .
Çàìå÷àíèå. Ïðîâåðêà ñóùåñòâîâàíèÿ õ è ó îáÿçàòåëüíà.
Åñëè íåìíîãî èçìåíèòü èñõîäíóþ çàäà÷ó, ïîëîæèâ â ïðàâîé
÷àñòè îãðàíè÷åíèÿ ÷èñëî 12, òî ìû ïîëó÷èì a Î [ -4; -3 2] .
Íî ìíîæåñòâî çíà÷åíèé â òàêîé ïîñòàíîâêå çàäà÷è îêàçûâàåòñÿ ïóñòûì.
(
)
Óïðàæíåíèå 4. Íàéäèòå ìíîæåñòâî çíà÷åíèé ôóíêöèè
z = x 2 + 2 y2 , åñëè x 2 - xy + 2y2 = 1 .
Îáúåäèíåíèå îáðàçîâ ïðîìåæóòêîâ ìîíîòîííîñòè.
Ýêñòðåìóìû
Äàëåêî íå äëÿ âñåõ ôóíêöèé ìû ñìîæåì ðåøèòü óðàâíåíèå
f ( x ) = a . Âîò ïðèìåð: y = (1 - x ) e - x . Çäåñü ìîæåò ïîìî÷ü
èññëåäîâàíèå ôóíêöèè ñ ïîìîùüþ ïðîèçâîäíîé.
Íî ñíà÷àëà ïðèäåòñÿ ââåñòè íîâûå îïðåäåëåíèÿ.
Ñóæåíèåì ôóíêöèè y = f ( x ) íà ìíîæåñòâî A Ì D [ f ]
íàçûâàåòñÿ ôóíêöèÿ y = f ( x ) , äëÿ êîòîðîé x Î A . Îáîçíà-
÷åíèå: y = f ( x ) . Ïîä÷åðêíåì, ÷òî ñóæåíèå ôóíêöèè ýòî
A
óæå äðóãàÿ ôóíêöèÿ. Ó íåå èìååòñÿ ñâîå ìíîæåñòâî çíà÷åíèé
E éë f
ù = {y Î R x Î A Í D [ f ] è y = f ( x )} . Îíî ÿâëÿåòñÿ
Aû
îáðàçîì ôóíêöèè f ( x ) íà ìíîæåñòâå À.
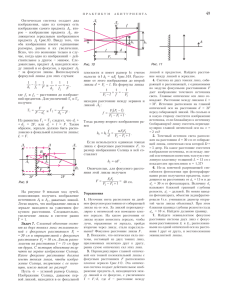
Òåîðåìà 2. Ïóñòü y = f ( x ) íåïðåðûâíà è ìîíîòîííà íà
""
ÊÂÀÍT 2007/¹4
îòðåçêå [a; b] . Òîãäà åñëè f ( x ) âîçðàñòàåò íà [a; b] , òî
E é f [a;b] ù = éë f (a ) ; f (b)ùû . Åñëè f ( x ) óáûâàåò íà [a; b] , òî
ë
û
é
ù
E f [a;b] = éë f (b ) ; f ( a ) ùû .
ë
û
Òåîðåìó èëëþñòðèðóþò ðèñóíêè 1 è 2.
Çàäà÷à 7. Íàéäèòå ìíîæåñòâî çíà÷åíèé ôóíêöèè
f ( x ) = 10 sin 2x + cos x .
Ðåøåíèå. Ïîñêîëüêó
f ¢ ( x ) = 20 cos 2x - 7 sin x = -40 sin2 x - 7 sin x + 20 = 0 ,
òî èìåþòñÿ äâå âîçìîæíîñòè:
4
3
1) sin x = - Þ cos x = ± ⇒
5
5
48 21
27
æ 4ö æ 3ö
æ 3ö
±
=±
⇒ f ( x ) = 20 ç - ÷ ç ± ÷ + 7 ç ± ÷ = m
;
è 5ø è 5ø
è 5ø
5
5
5
5
39
39
⇒ f (x) = ±
Þ cos x = ±
39 .
8
8
16
39 39 27
>
, ïîëó÷àåì îòâåò.
Çàìåòèâ, ÷òî
16
5
39
é 39
ù
39;
39 ú .
Îòâåò: ê 16
16
ë
û
2) sin x =
Ðèñ. 1
Ðèñ. 2
Îòðåçîê [a; b] ìîæíî çàìåíèòü ïðîìåæóòêàìè äðóãèõ
òèïîâ: èíòåðâàëàìè, ëó÷àìè. Ôîðìóëèðîâêà òåîðåìû èçìåíèòñÿ. Íàïðèìåð, åñëè f ( x ) âîçðàñòàåò íà [a; + ¥ ) , òî
)
E é f [a;+¥] ù = é f ( a ) ; lim f ( x ) .
ë
û êë
x ®+¥
Ïîòðåíèðóåìñÿ. Âû÷èñëèì îáðàç îòðåçêà [1; 4] äëÿ ôóíêöèè y = log1 2 x . Ýòà ôóíêöèÿ ÿâëÿåòñÿ óáûâàþùåé. Çíà÷åíèÿ â ãðàíè÷íûõ òî÷êàõ îòðåçêà ðàâíû 0 è 2. Ïîýòîìó
log1 2 x
= élog 4; log1 2 1ùû = [-2; 0] . Ïîêàæèòå ýòî íà ãðà[1;4] ë 1 2
ôèêå.
À òåïåðü èñïîëüçóåì ýòî äëÿ âû÷èñëåíèÿ E [ f ] . Ïðåäñòàâèì îáëàñòü îïðåäåëåíèÿ D [ f ] â âèäå îáúåäèíåíèÿ ïðîìåæóòêîâ ìîíîòîííîñòè Dk . Äëÿ êàæäîãî òàêîãî ïðîìåæóòêà
âû÷èñëèì åãî îáðàç Ek = E é f D ù . Òîãäà E [ f ] = U Ek .
ë kû
Çàäà÷à 6. Íàéäèòå ìíîæåñòâî çíà÷åíèé ôóíêöèè
y = (1 - x ) e - x .
Ðåøåíèå. Íàéäåì ïðîìåæóòêè ìîíîòîííîñòè. Ïîñêîëüêó
y ¢ = ( x - 2) e - x , òî ïðè x Î (-¥; 2] ôóíêöèÿ óáûâàåò, à ïðè
x Î [2; + ¥ ] âîçðàñòàåò, ò.å. õ = 2 òî÷êà ìèíèìóìà, òàê ÷òî
ymin = y (2) = - e -2 . Äàëåå,
lim (1 - x ) e - x = lim (1 + x ) e x = +¥ ,
x ®+¥
x ®-¥
lim (1 - x ) e - x = lim
x ®+¥
Ïîýòîìó
)
x ®+¥
(1 - x )
ex
)
E1 = E éê y ( -¥;2] ùú = éë - e -2; + ¥ ,
ë
û
=0.
Óïðàæíåíèÿ
Íàéäèòå ìíîæåñòâî çíà÷åíèé ôóíêöèè:
5. y = (1 + cos x ) sin x .
3
6. y = 8 3 cos x + 18 sin x .
7. y =
x 2 - 2x - 8
.
2 x +1
Ïðåäñòàâëåíèå â âèäå êîìïîçèöèè ôóíêöèé
Íàõîæäåíèå ìíîæåñòâà çíà÷åíèé ñóùåñòâåííî óïðîùàåòñÿ, åñëè óäàåòñÿ ïðåäñòàâèòü èññëåäóåìóþ ôóíêöèþ â âèäå
êîìïîçèöèè äðóãèõ ôóíêöèé: y = f ( x ) = g (h ( x )) . Òîãäà
E [ f ] ÿâëÿåòñÿ îáðàçîì ôóíêöèè g ( z ) íà ìíîæåñòâå
D [ g] I E [h] , ò.å. E [ f ] = E éê g D[g]I E[h] ùú .
ë
û
Çàäà÷à 8. Íàéäèòå ìíîæåñòâî çíà÷åíèé ôóíêöèè
y = log1 2 2x - x2 + 3 .
(
)
Ðåøåíèå. Äëÿ ôóíêöèè z = h ( x ) = 2 x - x2 + 3 = 4 - ( x 2
- 1) èìååì E [h] = ( -¥; 4] ; äëÿ ôóíêöèè y = g ( z ) = log1 2 z
èìååì D [ g ] = (0; + ¥ ) . Ïîëó÷èì D [ g] I E [h] = (0; 4] , çíà-
÷èò, E [ f ] = [-2; + ¥) .
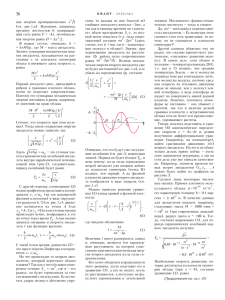
Ýòè ôîðìóëû ïðèîáðåòàþò íàãëÿäíîñòü ïðè èñïîëüçîâàíèè ãðàôèêîâ. Íà ðèñóíêå 3 èçîáðàæåí ãðàôèê ôóíêöèè
z = h ( x ) , ìíîæåñòâî çíà÷åíèé âûäåëåíî æèðíî. Ïîâåð-
E2 = E éê y [2;+¥) ùú =
ë
û
)
= éë - e -2; 0 . Òîãäà E = E1 U E2 = é - e -2; + ¥ . Íàðèñóéòå ýñë
êèç ãðàôèêà ôóíêöèè.
Òåîðåìà 3. Åñëè ôóíêöèÿ f ( x ) íåïðåðûâíà íà îòðåçêå
ù
f ( x ) ; max f ( x ) ú .
[a; b] , òî E [ f ] = éê xmin
x Î[a;b]
ë Î[a;b]
û
Äëÿ îòûñêàíèÿ ìíîæåñòâà çíà÷åíèé íóæíî âû÷èñëèòü
íàèìåíüøåå è íàèáîëüøåå çíà÷åíèÿ ôóíêöèè íà îòðåçêå. Ýòè
çíà÷åíèÿ çàäàþò ãðàíèöû ìíîæåñòâà çíà÷åíèé. Ïîèñê íàèìåíüøåãî è íàèáîëüøåãî çíà÷åíèé ôóíêöèè íà îòðåçêå
ïðîâîäèòñÿ ïî èçâåñòíîé ñõåìå. Âû÷èñëÿþòñÿ çíà÷åíèÿ
ôóíêöèè â êðèòè÷åñêèõ òî÷êàõ (òî÷êàõ, â êîòîðûõ ïðîèçâîäíàÿ ôóíêöèè îáðàùàåòñÿ â íîëü èëè íå ñóùåñòâóåò), à òàêæå
â ãðàíè÷íûõ òî÷êàõ îòðåçêà. Èç ýòèõ çíà÷åíèé âûáèðàþòñÿ
ìèíèìàëüíîå è ìàêñèìàëüíîå.
Äëÿ ïåðèîäè÷åñêèõ ôóíêöèé äîñòàòî÷íî âû÷èñëèòü çíà÷åíèÿ ôóíêöèè â êðèòè÷åñêèõ òî÷êàõ.
Ðèñ. 3
Ðèñ. 4
íåì îñü z èç âåðòèêàëüíîãî ïîëîæåíèÿ â ãîðèçîíòàëüíîå è
ïîìåñòèì åå íà ðèñóíêå 4, ãäå ïîêàçàí ãðàôèê y = g ( z ) è
âûäåëåíà îáëàñòü îïðåäåëåíèÿ ýòîé ôóíêöèè. Âèäíî, ÷òî
îáðàçîì ïðîìåæóòêà (0; 4] ÿâëÿåòñÿ ëó÷ [ -2; + ¥ ) .
Äëÿ ñðàâíåíèÿ ðåøèòå ýòó çàäà÷ó ïåðâûì è âòîðûì ìåòîäàìè.
ÏÐÀÊÒÈÊÓÌ
Äàâàéòå òåïåðü åùå ðàç ðåøèì çàäà÷ó 3. Ôóíêöèÿ
y = 15 + 2x - x2 = f ( x ) ïðåäñòàâëÿåòñÿ â âèäå f ( x ) =
= g (h ( x )) , ãäå y = g ( z ) =
2
= 16 - ( x - 1) . Äàëåå,
z , z = h ( x ) = - x2 + 2x + 15 =
E [h] = (-¥; 16] ;
D [ g] = [0; + ¥ ) ;
E [h] I D [ g] = [0; 16] . Ôóíêöèÿ g ( z ) âîçðàñòàþùàÿ, ïîýòî-
ìó Ee [ f ] = éë g (0) ; g (16) ùû = [0; 4] . (Ñàìîñòîÿòåëüíî íàðèñóéòå
ãðàôèêè â ñèñòåìàõ êîîðäèíàò Îõz è Oyz.)
Óïðàæíåíèÿ
Íàéäèòå ïåðâûì è òðåòüèì ìåòîäàìè ìíîæåñòâî çíà÷åíèé
ôóíêöèè:
æ 2x + 5
ö
- 1÷ .
è x -1
ø
Îòâåò: [ -1; 2) .
Ìîæíî âñòðåòèòü ðåêîìåíäàöèè äëÿ âû÷èñëåíèÿ ãðàíèö
èçìåíåíèÿ ôóíêöèè ñ èñïîëüçîâàíèåì êëàññè÷åñêèõ íåðàâåíñòâ, íàïðèìåð íåðàâåíñòâà ìåæäó ñðåäíèì àðèôìåòè÷åñêèì è ñðåäíèì ãåîìåòðè÷åñêèì. Äëÿ äâóõ ïåðåìåííûõ îíî
a+b
èìååò âèä
³ ab , a, b ³ 0 . Ñ åãî ïîìîùüþ ìîæíî,
2
1
íàïðèìåð, ïîêàçàòü, ÷òî x + ³ 2 , x > 0. Íî ñ ïîìîùüþ
x
ýòîãî íåðàâåíñòâà ìîæíî ïîëó÷èòü, âîîáùå ãîâîðÿ, ëèøü
îöåíêó äëÿ ìíîæåñòâà çíà÷åíèé.  äàííîì ñëó÷àå îíî
ñîâïàäàåò ñ ìíîæåñòâîì çíà÷åíèé [2; + ¥) . À ñêàæåì, äëÿ
ôóíêöèè
8. y = lg ç
9. y =
y=
2x + 1
-1.
x-3
Çàäà÷à 9. Íàéäèòå ìíîæåñòâî çíà÷åíèé ôóíêöèè
y = 2 cos x - cos 2x .
Ðåøåíèå. Íà ïåðâûé âçãëÿä íå âèäíî, êîìïîçèöèåé êàêèõ
ôóíêöèé ÿâëÿåòñÿ y ( x ) . Ïðåîáðàçóåì åå: y = 2 cos x 2
- cos 2x = 2 cos x - 2 cos2 x + 1 . Äàëåå, y ( z) = -2z + 2z +
2
1ö
3
æ
+ 1 = -2 ç z - ÷ + ; z = cos x . Òîãäà E [ z] = [ -1; 1] . Èùåì
è
2ø
2
íàèáîëüøåå è íàèìåíüøåå çíà÷åíèÿ y ( z ) íà îòðåçêå [-1; 1] .
Ïîëó÷àåì îòâåò: [ -3; 3 2] .
11. y = 4 cos2 x + 3 sin2 2x .
12. y = 2 sin x cos 2x + 7 sin x .
Åñëè èñõîäíàÿ ôóíêöèÿ ïðåäñòàâëåíà êàê êîìïîçèöèÿ
íåñêîëüêèõ ôóíêöèé: y = f1 K fn -1 (fn ( x ))K , òî ñíà÷àëà
íóæíî âû÷èñëèòü ìíîæåñòâî çíà÷åíèé âíóòðåííåé ôóíêöèè
En = E ëé fn ( x ) ûù . Çàòåì âû÷èñëèòü îáðàç En -1 = fn -1 (D [fn -1 ] I
I En ) è òàê äàëåå.
(
)
Óïðàæíåíèå 13. Íàéäèòå ìíîæåñòâî çíà÷åíèé ôóíêöèè
2
y = 7 + 3x - x - 2 - x + 3x + 4 .
Çàäà÷à 10. Ïðè êàêèõ çíà÷åíèÿõ à óðàâíåíèå
2
)= a +
2 x2 + 2 x2 + 4
=
2x 2 + 8
+
x2 + 2
x2 + 2
2x2 + 8
(
3 sin 2 2 x - x
Òðèãîíîìåòðè÷åñêèå ïîäñòàíîâêè
Ïóñòü äëÿ ôóíêöèè y = f ( x ) óäàëîñü íàéòè ôóíêöèþ
x = g (t ) , t Î D [ g] òàêóþ, ÷òî D [ f ] Ì E [ g] , à íîâàÿ ôóíê-
öèÿ y = f (g (t )) = p (t ) ïðîùå äëÿ èññëåäîâàíèÿ, ÷åì èñõîä-
íàÿ. Ïðè ýòîì E [ f ] = E [ p] .  êà÷åñòâå x = g (t ) ïîäáèðàþò
òðèãîíîìåòðè÷åñêóþ ôóíêöèþ. Ñàì âèä òðèãîíîìåòðè÷åñêèõ ôîðìóë ïîçâîëÿåò äîáèòüñÿ ñóùåñòâåííûõ óïðîùåíèé.
Çàäà÷à 11. Íàéäèòå âñå çíà÷åíèÿ à, ïðè êîòîðûõ óðàâíå 1 1
Ðåøåíèå. Òàê êàê x ∈ − ; , âûáåðåì ôóíêöèþ
2 2
1
π π
x = sin t , t ∈ − ; . Òîãäà
2
2 2
Íàéäèòå ìíîæåñòâî çíà÷åíèé ôóíêöèè:
(
)
íèå x 1 − 4x 2 (1 − 8x 2 ) = a èìååò ðåøåíèå.
Óïðàæíåíèÿ
2 cos2 2 2 x - x
(
2 3x 2 + 10
æ 3 2 5ù
; ú Ì [2; + ¥) (äîêàæèòå ýòî).
ìíîæåñòâî çíà÷åíèé ç
è 2 2û
10. y = log 3 (1 - 2 cos x ) .
2
"#
ÀÁÈÒÓÐÈÅÍÒÀ
2
+1
) èìååò õîòÿ áû îäíî
ðåøåíèå?
Ðåøåíèå. Ïåðåôîðìóëèðóåì çàäà÷ó: íàéäåì ìíîæåñòâî
(
çíà÷åíèé ôóíêöèè f ( x ) = 2 cos2 22 x - x
2
)-
(
3 sin 2 × 22 x - x
Ïðåäñòàâèì åå êàê êîìïîçèöèþ ôóíêöèé:
2
).
f (u ) = 2 cos2 (u ) - 3 sin (2u ) =
1
1
1
sin t 1 − sin2 t (1 − 2 sin2 t ) = sin t cos t cos 2t = sin 4t .
2
8
2
1 1
Îòâåò: a ∈ − ; .
8 8
Çàìå÷àíèå. Áëàãîäàðÿ óäà÷íîìó âûáîðó îáëàñòè îïðåäåëåíèÿ äëÿ ôóíêöèè g (t ) ìû ñóùåñòâåííî ñîêðàòèëè ðåøåx=
íèå:
1 − sin2 t = cos t = cos t , òàê êàê
Ìîæíî äàòü ñëåäóþùèå ðåêîìåíäàöèè äëÿ óïðîùåíèÿ
ðàäèêàëîâ:
π π
a2 − x 2 x = a sin t, t ∈ − ; èëè x = a cos t, t ∈ [0; π] ;
2 2
π π
2
2
a + x x = atgt, t ∈ − ; èëè x = actgt, t ∈ (0; π ) ;
2 2
a
π π
, t ∈ − ; \ {0} èëè
sin t
2 2
π
a
, t ∈ [0; π] \
x=
.
cos t
2
{}
πö
æ
z
= 1 + cos (2u ) - 3 sin (2u ) = 1 + 2 cos ç 2u + ÷ ; u ( z ) = 2 ;
è
3ø
2
Òîãäà E [ z] = ( -¥; 1] , E [u] = (0; 2] . (Íàðèñóéòå ñîîòâåòñòâóþùèå ãðàôèêè.)
πö 1
π
π π
æ
Ïîñêîëüêó 4 + ³ 2u + > , òî -1 £ cos çè 2u + ÷ø < , è
3
2
3
3 3
E ( f ) = [-1; 2) .
ïðè
π π
t ∈ − ; .
2 2
x 2 − a2 x =
z ( x ) = 2x - x 2 = 1 - ( x - 1) .
cos t ³ 0
Íî ýòî íå áîëåå ÷åì ðåêîìåíäàöèè. Îíè ìîãóò è íå ïðèâåñòè
ê óñïåõó.
Óïðàæíåíèÿ
Íàéäèòå ìíîæåñòâî çíà÷åíèé ôóíêöèè:
14. y =
x x2 + 4 - x 2
x2 + 4
.
"$
ÊÂÀÍT 2007/¹4
15. y =
x
2
x - x x -1
ùåé íà îñè Îõ, äî òî÷åê A (1; 3 ) è B (3 2; − 3 3 2 ) . Ýòà
.
ñóììà íå ìåíüøå, ÷åì äëèíà îòðåçêà AB = 19 .
)
æ 5 - 12x
ö
-5 .
16. y = log16 ç
÷ø
è x2 + 1
Çàäà÷à 12. Íàéäèòå ìíîæåñòâî çíà÷åíèé ôóíêöèè
z = y 1 − x 2 + x 4 − y2 .
π π
Ðåøåíèå. Ïóñòü x = sin u , y = 2 sin v , u, v ∈ − ; .
2 2
Òîãäà z = 2 sin v cos u + 2 sin u cos v = 2 sin (u + v ) .
Îòâåò: [−2;2] .
Åùå ðàç ðåøèì çàäà÷ó 5.
Çàäà÷à 5. ×èñëà õ è ó óäîâëåòâîðÿþò ðàâåíñòâó
7x 2 − 4xy + 4y2 = 12. Íàéäèòå âñå çíà÷åíèÿ, êîòîðûå ìîæåò ïðèíèìàòü ñóììà x2 + y2 .
Ðåøåíèå. Ïóñòü x = r cos ϕ , y = r sin ϕ , r ≥ 0 , ϕ ∈ [0;2π ) .
Òîãäà x2 + y2 = r 2 . Ïðåîáðàçóåì îãðàíè÷åíèå: 7r 2 cos2 ϕ −
− 4r 2 sin ϕ cos ϕ + 4r 2 sin2 ϕ = 12 , r 2 (3 cos2 ϕ − 2 sin 2ϕ + 4 ) =
24
,
5 cos (2ϕ + ψ ) + 11
3
24 3
24
=
;
;4 .
ãäå ψ = arcos , E [r 2 ] =
5
5 + 11 −5 + 11 2
3
Îòâåò: ; 4 .
2
= 12, r 2 (11 + 3 cos 2ϕ − 4 sin 2ϕ ) = 24 , r 2 =
Óïðàæíåíèå 4. Íàéäèòå ìíîæåñòâî çíà÷åíèé ôóíêöèè
2
2
z = x2 + 2y2 , åñëè x - xy + 2y = 1 .
Ãåîìåòðè÷åñêàÿ èíòåðïðåòàöèÿ
Åñëè óäàåòñÿ óâèäåòü â çàäà÷å íà âû÷èñëåíèå ìíîæåñòâà
çíà÷åíèé ôóíêöèè ãåîìåòðè÷åñêîå ñîäåðæàíèå, òî ýòî ïîçâîëÿåò ñóùåñòâåííî ïðîäâèíóòüñÿ â ðåøåíèè çàäà÷è.
Çàäà÷à 3. Íàéäèòå ìíîæåñòâî çíà÷åíèé ôóíêöèè
y = 15 + 2x − x 2 .
Ðåøåíèå. Äàííîå óðàâíåíèå ðàâíîñèëüíî ñèñòåìå
Îòâåò: 19; + ∞ .
Çàäà÷à 14. Ïóñòü õ è ó óäîâëåòâîðÿþò ñèñòåìå
y − x ≤ 5,
y + 4x ≤ −5,
3y + 2x ≥ −5.
Íàéäèòå âñå çíà÷åíèÿ, êîòîðûå ìîãóò ïðèíèìàòü x2 + y2
y
è
.
x
Ðåøåíèå. Ñèñòåìà íåðàâåíñòâ îïèñûâàåò òðåóãîëüíèê íà
ïëîñêîñòè õÎó. Åãî âåðøèíû: A ( −4;1) , B ( −2;3 ) , C ( −1; − 1)
(ðèñ.6); x2 + y2 ýòî êâàäðàò ðàññòîÿíèÿ îò òî÷êè òðåóãîëüíèêà (x; y) äî íà÷àëà
êîîðäèíàò. Íàèìåíüøåå ðàññòîÿíèå ðàññòîÿíèå äî ïðÿìîé
ÂÑ.
Âûðàæåíèå
2
x2 + ( −4 x − 5 ) = 17 x2 + 40 x +
+ 25 ïðèíèìàåò íàèìåíüøåå
25
20
∈
ïðè x = −
17
17
∈ [−2; − 1] . Íàèáîëüøåå ðàññòîÿíèå äëèíà îòðåçêà Ðèñ. 6
y
ÀÎ = 17. Ïîñêîëüêó
x
òàíãåíñ óãëà íàêëîíà ïðÿìîé, ïðîõîäÿùåé ÷åðåç íà÷àëî
êîîðäèíàò è òî÷êó òðåóãîëüíèêà ( x; y ) , íàèáîëüøåå è íàèìåíüøåå çíà÷åíèÿ äîñòèãàþòñÿ íà ïðÿìûõ ÑÎ è ÂÎ.
çíà÷åíèå
25
3
Îòâåò: ;17 , − ;1 .
17
2
Óïðàæíåíèå 17. Ïóñòü õ è ó óäîâëåòâîðÿþò íåðàâåíñòâó
( x − 1) + y = 4 ,
y ≥ 0.
3 x - 6 + 2 y + 3 £ 12 . Íàéäèòå âñå çíà÷åíèÿ, êîòîðûå ìîãóò
y
.
ïðèíèìàòü x2 + y2 è
x
Óðàâíåíèå ñèñòåìû óðàâíåíèå îêðóæíîñòè ðàäèóñà 4 ñ
öåíòðîì â òî÷êå (1;0 ) , íåðàâåíñòâî âåðõíÿÿ ïîëóïëîñêîñòü. Ïåðåñå÷åíèå äâóõ ýòèõ ìíîæåñòâ ïîêàçàíî íà ðèñóíêå
Çàìå÷àíèå îò ðåäàêöèè. Ìåòîäû ðåøåíèÿ çàäà÷, ñâÿçàííûõ ñ ìíîæåñòâîì çíà÷åíèé ñåìåéñòâ ôóíêöèé, çàâèñÿùèõ
îò ïàðàìåòðà, ðàññìîòðåíû òàêæå â ñòàòüå Â.Ãîëóáåâà è
Ê.Ìîñåâè÷à «Ñåìåéñòâà ôóíêöèé», îïóáëèêîâàííîé â æóðíàëå «Êâàíò» ¹2 çà 2006 ãîä.
2
2
2
Èíôîðìàöèþ î æóðíàëå «Êâàíò» è íåêîòîðûå
ìàòåðèàëû èç æóðíàëà ìîæíî íàéòè â ÈÍÒÅÐÍÅÒÅ ïî
àäðåñàì:
Ðèñ. 5
5. Îðòîãîíàëüíàÿ ïðîåêöèÿ âåðõíåé ïîëóîêðóæíîñòè íà îñü
îðäèíàò ÿâëÿåòñÿ îòðåçêîì [0; 4] .
Çàäà÷à 13. Íàéäèòå ìíîæåñòâî çíà÷åíèé ôóíêöèè
y = x 2 − 2x + 4 + x 2 − 3x + 9 .
Ðåøåíèå. Ôóíêöèÿ
2
y = ( x − 1) + (0 − 3 ) +
2
( x − 3 2 )2 + (0 + 3
3 2)
2
ïðåäñòàâëÿåò ñîáîé ñóììó ðàññòîÿíèé îò òî÷êè ( x;0 ) , ëåæà-
Ðåäàêöèÿ æóðíàëà «Êâàíò»
kvant.info
Ìîñêîâñêèé öåíòð íåïðåðûâíîãî ìàòåìàòè÷åñêîãî
îáðàçîâàíèÿ
kvant.mccme.ru
Ìîñêîâñêèé äåòñêèé êëóá «Êîìïüþòåð»
math.child.ru
Êîñòðîìñêîé öåíòð äîïîëíèòåëüíîãî îáðàçîâàíèÿ
«Ýâðèêà»
ceemat.ru