Решения. 10 класс
реклама

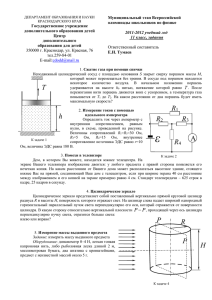
10 класс 10.1 Тело брошено вертикально вверх с начальной скоростью v0. Когда оно достигло высшей точки траектории, из той же начальной точки с той же начальной скоростью брошено вверх другое тело. На какой высоте h они встретятся? Решение Используя известную формулу равноускоренного движения V 2 V02 S 2a и учитывая, что в верхней точке v = 0, получаем V2 hmax 0 . 2g Если отсчитывать время от момента бросания второго тела, то уравнения движения тел следует записать в виде: gt 2 gt 2 h1 hmax ; h2 V0t . 2 2 Приравнивая h1 h2 h (в момент встречи), получаем hmax V0 3 V02 . t ; h 8 g V0 2g 3 V02 Ответ: h . 8 g 10.2 На тележке установлен штатив, на котором подвешен шарик на нити. Тележка движется горизонтально с ускорением а. Найдите угол α отклонения нити от вертикали и силу Т натяжения нити. Решение На шарик действуют две силы: сила тяжести mg и натяжение Т нити (см. рисунок). Их равнодействующая F сообщает шарику такое же ускорение, какое имеет тележка, т.е. F ma. Следовательно, a tg . g Величину силы Т находим из теоремы Пифагора: T m g 2 a2 . Ответ: tg a , T m g 2 a2 . g 10.3 Санки массой m = 20 кг поднимают по гладкому склону на высоту h = 2,5 м, прикладывая силу F = 300 Н, направленную вдоль склона. Санки движутся с ускорением а = 3 м/с2. Какая работа А совершается при подъеме? Чему равно изменение потенциальной энергии ΔWp санок? Чему равна кинетическая энергия Wk санок на вершине? Решение Изменение потенциальной энергии санок будет равно W p mgh 490 Дж. По второму закону Ньютона получим: ma F mg sin . Отсюда F ma . mg По формулам равноускоренного движения: at 2 l ; V at . 2 Отсюда V 2 2al . Из рисунка видно, что h l . sin Подставляя, получим 2ahmg V2 . F ma Тогда кинетическая энергия санок на вершине mV 2 m2 gha Wk 122,5 Дж . 2 F ma По закону сохранения энергии A Wk W p 122,5 490 612,5 Дж. sin Ответ: W p 490 Дж, Wk 122,5 Дж, A 612,5 Дж. 10.4 Озеро со средней глубиной h = 5 м и площадью S = 4 км2 «посолили», бросив кристаллик поваренной соли NaCl массой m = 10 мг. Спустя длительное время из озера зачерпнули стакан воды объемом V = 200 см3. Сколько ионов натрия оказалось в этом стакане? Решение Общее количество ионов натрия в кристаллике соли m N0 N A , где – молярная масса NaCl. За длительное время ионы натрия равномерно распределяются по всему объему озера, равному hS. Значит концентрация ионов в стакане и в озере одинакова: N N n 0 , V hS где N – искомое количество ионов в стакане. Отсюда N N0 mVN A V 10 9 . hS hS Ответ: N 109. 10.5 В цилиндре под поршнем площадью S = 100 см2 и массой m1 = 50 кг находится воздух при температуре t1 = 7 ºС. Поршень находится на высоте h1 = 60 см от дна цилиндра. Воздух в цилиндре нагревают до t2 = 47 ºС, а на поршень ставят гирю массой m2 = 50 кг. На сколько опустится или поднимется поршень? Атмосферное давление р0 = 100 кПа, трением поршня о стенки цилиндра можно пренебречь. Решение Запишем условие равновесия поршня в начальном и конечном положениях: m1g p0 S p1S , m1g m2 g p0 S p2 S . Здесь р1 и р2 – начальное и конечное давления воздуха в цилиндре. Эти величины связаны между собой уравнением Клапейрона: P1V1 P2V21 . T1 T2 Здесь V1 Sh1 и V2 S h1 x – соответственно начальный и конечный объем воздуха в цилиндре, х – перемещение поршня. Отсюда m1 g p0 S T 19см . x h1 1 2 T m g m g p s 1 1 2 0 Таким образом, поршень опустится на 19 см. Ответ: Поршень опустится на 19 см.