МОДЕЛИРОВАНИЕ СТРОЕНИЯ ПОЛИКОНДЕНСАТОВ
реклама
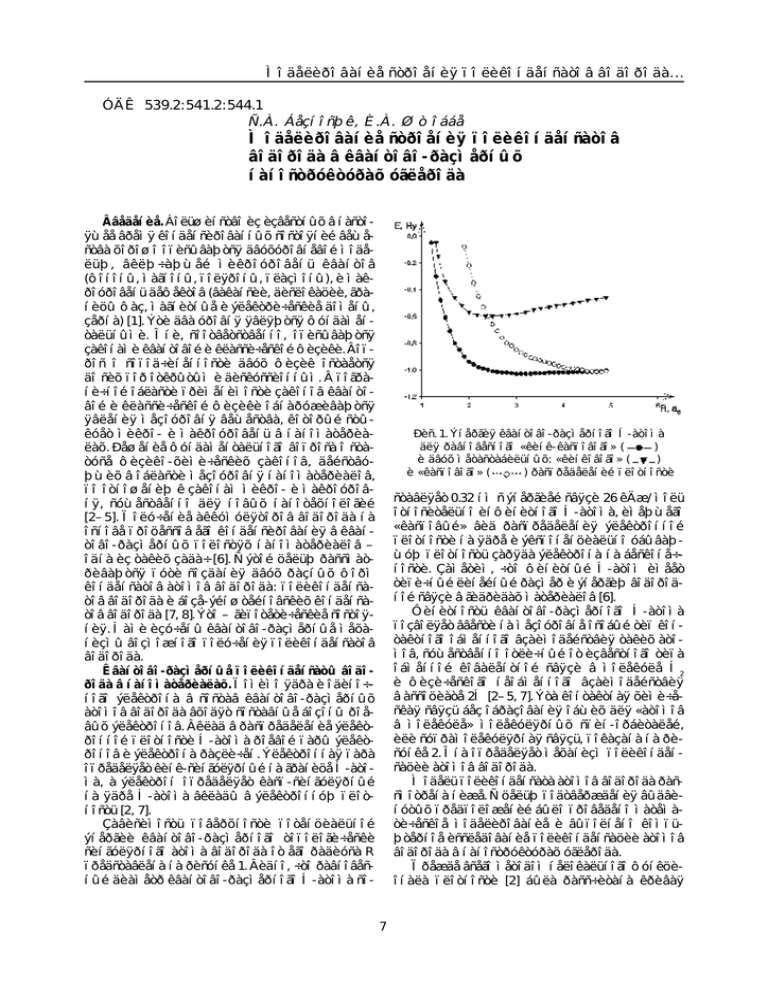
Ìîäåëèðîâàíèå ñòðîåíèÿ ïîëèêîíäåíñàòîâ âîäîðîäà... ÓÄÊ 539.2:541.2:544.1 Ñ.À. Áåçíîñþê, È.À. Øòîááå Ìîäåëèðîâàíèå ñòðîåíèÿ ïîëèêîíäåíñàòîâ âîäîðîäà â êâàíòîâî-ðàçìåðíûõ íàíîñòðóêòóðàõ óãëåðîäà Ââåäåíèå. Áîëüøèíñòâî èç èçâåñòíûõ â íàñòîÿùåå âðåìÿ êîíäåíñèðîâàííûõ ñîñòîÿíèé âåùåñòâà õîðîøî îïèñûâàþòñÿ äâóõóðîâíåâîé ìîäåëüþ, âêëþ÷àþùåé ìèêðîóðîâåíü êâàíòîâ (ôîíîíû, ìàãíîíû, ïîëÿðîíû, ïëàçìîíû), è ìàêðîóðîâåíü äåôåêòîâ (âàêàíñèè, äèñëîêàöèè, ãðàíèöû ôàç, ìàãíèòíûå è ýëåêòðè÷åñêèå äîìåíû, çåðíà) [1]. Ýòè äâà óðîâíÿ ÿâëÿþòñÿ ôóíäàìåíòàëüíûìè. Îíè, ñîîòâåòñòâåííî, îïèñûâàþòñÿ çàêîíàìè êâàíòîâîé è êëàññè÷åñêîé ôèçèêè. Âîïðîñ î ñîïîä÷èíåííîñòè äâóõ ôèçèê îñòàåòñÿ äî ñèõ ïîð îòêðûòûì è äèñêóññèîííûì.  ïîãðàíè÷íîé îáëàñòè ïðèìåíèìîñòè çàêîíîâ êâàíòîâîé è êëàññè÷åñêîé ôèçèêè îáíàðóæèâàþòñÿ ÿâëåíèÿ ìåçîóðîâíÿ âåùåñòâà, êîòîðûé ñòûêóåò ìèêðî- è ìàêðîóðîâåíü â íàíîìàòåðèàëàõ. Ðåøåíèå ôóíäàìåíòàëüíîãî âîïðîñà î ñòàòóñå ôèçèêî-õèìè÷åñêèõ çàêîíîâ, äåéñòâóþùèõ â îáëàñòè ìåçîóðîâíÿ íàíîìàòåðèàëîâ, ïî îòíîøåíèþ ê çàêîíàì ìèêðî- è ìàêðîóðîâíÿ, ñóùåñòâåííî äëÿ íîâûõ íàíîòåõíîëîãèé [2–5]. Ïîëó÷åíèå àêêóìóëÿòîðîâ âîäîðîäà íà îñíîâå ïðîöåññîâ åãî êîíäåíñèðîâàíèÿ â êâàíòîâî-ðàçìåðíûõ ïîëîñòÿõ íàíîìàòåðèàëîâ – îäíà èç òàêèõ çàäà÷ [6]. Ñ ýòîé öåëüþ ðàññìàòðèâàþòñÿ ïóòè ñîçäàíèÿ äâóõ ðàçíûõ ôîðì êîíäåíñàòîâ àòîìîâ âîäîðîäà: ïîëèêîíäåíñàòîâ âîäîðîäà è áîçå-ýéíøòåéíîâñêèõ êîíäåíñàòîâ âîäîðîäà [7, 8]. Ýòî – ãèïîòåòè÷åñêèå ñîñòîÿíèÿ. Íàìè èçó÷åíû êâàíòîâî-ðàçìåðíûå ìåõàíèçìû âîçìîæíîãî ïîëó÷åíèÿ ïîëèêîíäåíñàòîâ âîäîðîäà. Êâàíòîâî-ðàçìåðíûå ïîëèêîíäåíñàòû âîäîðîäà â íàíîìàòåðèàëàõ. Ïîìèìî ÿäðà è îäèíî÷íîãî ýëåêòðîíà â ñîñòàâ êâàíòîâî-ðàçìåðíûõ àòîìîâ âîäîðîäà âõîäÿò ñîñòàâíûå áîçîíû ðîåâûõ ýëåêòðîíîâ. Âêëàä â ðàñïðåäåëåíèå ýëåêòðîííîé ïëîòíîñòè Í-àòîìà ðîåâîé ïàðû ýëåêòðîíîâ è ýëåêòðîíà ðàçëè÷åí. Ýëåêòðîííàÿ ïàðà îïðåäåëÿåò êèíê-ñèíãóëÿðíûé íà ãðàíèöå Í-àòîìà, à ýëåêòðîí îïðåäåëÿåò êàñï-ñèíãóëÿðíûé íà ÿäðå Í-àòîìà âêëàäû â ýëåêòðîííóþ ïëîòíîñòü [2, 7]. Çàâèñèìîñòü ïîâåðõíîñòè ïîòåíöèàëüíîé ýíåðãèè êâàíòîâî-ðàçìåðíîãî òîïîëîãè÷åñêè ñèíãóëÿðíîãî àòîìà âîäîðîäà îò åãî ðàäèóñà R ïðåäñòàâëåíà íà ðèñóíêå 1. Âèäíî, ÷òî ðàâíîâåñíûé äèàìåòð êâàíòîâî-ðàçìåðíîãî Í-àòîìà ñî- Ðèñ. 1. Ýíåðãèÿ êâàíòîâî-ðàçìåðíîãî Í-àòîìà äëÿ ðàâíîâåñíîãî «êèíê-êàñïîâîãî» ( ) è äâóõ ìåòàñòàáèëüíûõ: «êèíêîâîãî» ( ) è «êàñïîâîãî» ( ) ðàñïðåäåëåíèé ïëîòíîñòè ñòàâëÿåò 0.32 íì ñ ýíåðãèåé ñâÿçè 26 êÄæ/ìîëü îòíîñèòåëüíî èíôèíèòíîãî Í-àòîìà, èìåþùåãî «êàñïîâûé» âèä ðàñïðåäåëåíèÿ ýëåêòðîííîé ïëîòíîñòè íà ÿäðå è ýêñïîíåíöèàëüíî óáûâàþùóþ ïëîòíîñòü çàðÿäà ýëåêòðîíà íà áåñêîíå÷íîñòè. Çàìåòèì, ÷òî ôèíèòíûé Í-àòîì èìååò òèïè÷íûé ëèíåéíûé ðàçìåð è ýíåðãèþ âîäîðîäíîé ñâÿçè â ãèäðèäàõ ìàòåðèàëîâ [6]. Ôèíèòíîñòü êâàíòîâî-ðàçìåðíîãî Í-àòîìà ïîçâîëÿåò ââåñòè íà ìåçîóðîâíå îñîáûé òèï êîíòàêòíîãî îáìåííîãî âçàèìîäåéñòâèÿ òàêèõ àòîìîâ, ñóùåñòâåííî îòëè÷íûé îò èçâåñòíîãî òèïà îáìåííîé êîâàëåíòíîé ñâÿçè â ìîëåêóëå Í2 è ôèçè÷åñêîãî íåîáìåííîãî âçàèìîäåéñòâèÿ â àññîöèàòå 2Í [2–5, 7]. Ýòà êîíòàêòíàÿ õèìè÷åñêàÿ ñâÿçü áåç îáðàçîâàíèÿ îáùèõ äëÿ «àòîìîâ â ìîëåêóëå» ìîëåêóëÿðíûõ ñïèí-îðáèòàëåé, èëè ñóïðàìîëåêóëÿðíàÿ ñâÿçü, ïîêàçàíà íà ðèñóíêå 2. Îíà îïðåäåëÿåò ìåõàíèçì ïîëèêîíäåíñàöèè àòîìîâ âîäîðîäà. Ìîäåëü ïîëèêîíäåíñàòà àòîìîâ âîäîðîäà ðàññìîòðåíà íèæå. Ñ öåëüþ ïîäòâåðæäåíèÿ âûäâèíóòûõ ïðåäïîëîæåíèé áûëî ïðîâåäåíî ìàòåìàòè÷åñêîå ìîäåëèðîâàíèå è âûïîëíåíî êîìïüþòåðíîå èññëåäîâàíèå ïîëèêîíäåíñàöèè àòîìîâ âîäîðîäà â íàíîñòðóêòóðàõ óãëåðîäà. Ïðåæäå âñåãî ìåòîäîì íåëîêàëüíîãî ôóíêöèîíàëà ïëîòíîñòè [2] áûëà ðàññ÷èòàíà êðèâàÿ 7 ÕÈÌÈß Ðèñ. 2. Êâàíòîâî-ðàçìåðíûå ìåõàíèçìû êîíòàêòíîé õèìè÷åñêîé ñâÿçè áåç îáðàçîâàíèÿ îáùèõ äëÿ «àòîìîâ â ìîëåêóëå» ìîëåêóëÿðíûõ ñïèí-îðáèòàëåé Ðèñ. 4. Ñóïðàìîëåêóëÿðíûå êîíòàêòíûå ñâÿçè ìåæäó àòîìàìè âîäîðîäà â ôèçè÷åñêè àäñîðáèðîâàííîì ìîíîñëîå âîäîðîäà ýíåðãèè àòîì-àòîìíîãî ñóïðàìîëåêóëÿðíîãî êîíòàêòíîãî îáìåííîãî âçàèìîäåéñòâèÿ Í–Í â çàâèñèìîñòè îò ìåæàòîìíîãî ðàññòîÿíèÿ. Áûëè ïîëó÷åíû ñëåäóþùèå ðàâíîâåñíûå ïàðàìåòðû ñâÿçè: ìåæúÿäåðíîå ðàññòîÿíèå R0 = 0.10 íì è ýíåðãèÿ ñâÿçè Åñâÿçè = 51 êÄæ/ìîëü. Íàìè áûëè èññëåäîâàíû äâå ôèçè÷åñêèå ìîäåëè, ðàçëè÷àþùèåñÿ ïîëîæåíèåì àòîìîâ âîäîðîäà îòíîñèòåëüíî óãëåðîäíûõ àòîìîâ â ãðàôåíîâûõ ïëîñêîñòÿõ óãëåðîäà: 1. Ôèíèòíûé àòîì âîäîðîäà îáðàçóåò ñ àòîìîì óãëåðîäà êîíòàêòíóþ îáìåííóþ ñâÿçü. Àòîìû óãëåðîäà îáðàçóþò ñóïðàìîëåêóëÿðíóþ ñâÿçü ñ õèìè÷åñêè àäñîðáèðîâàííûì ñëîåì Í-àòîìîâ (ðèñ. 3). äîðîäà ïðîâåäåíû êîìïüþòåðíûå ðàñ÷åòû ñòðóêòóðû àíòèôåððîìàãíèòíî óïîðÿäî÷åííûõ ïî ñïèíó ñóïðàìîëåêóëÿðíûõ ïî ñâÿçè ñèñòåì. Áûëè îïðåäåëåíû ïàðàìåòðû ñâÿçè êëàñòåðîâ âîäîðîäà ñ ó÷åòîì âçàèìîäåéñòâèé äî òðåòüåé è îäèííàäöàòîé êîîðäèíàöèîííîé ñôåðû Í-àòîìà. Ïîëèíîìíàÿ àïïðîêñèìàöèÿ ðàñ÷åòíîé êðèâîé ïîòåíöèàëüíîé ýíåðãèè êîíòàêòíîé ñâÿçè Í–Í èìååò àíàëèòè÷åñêèé âèä: . Ýòîò ìîäåëüíûé ïîòåíöèàë èñïîëüçîâàí äëÿ ïîñòðîåíèÿ êðèâîé ïîòåíöèàëüíîé ýíåðãèè ïîëèêîíäåíñàòà âîäîðîäà â ðàñ÷åòå íà ïàðó àòîìîâ ñóïðàìîëåêóë Í–Í â çàâèñèìîñòè îò ìåæàòîìíîãî ðàññòîÿíèÿ r (ðèñ. 5). Ýòó êðèâóþ óäîáíî ñðàâíèâàòü ñ ïðîôèëåì ïîâåðõíîñòè ïîòåíöèàëüíîé ýíåðãèè ìîëåêóëû Í2 â ãàçîâîé ôàçå.  ðåçóëüòàòå ðàñ÷åòà íàìè îïðåäåëåíû ðàâíîâåñíûå ïàðàìåòðû êîíòàêòíîé ñâÿçè Í – Í ïðè Ðèñ. 3. Ñóïðàìîëåêóëÿðíûå êîíòàêòíûå ñâÿçè ìåæäó àòîìàìè óãëåðîäà è âîäîðîäà â õèìè÷åñêè àäñîðáèðîâàííîì ìîíîñëîå âîäîðîäà 2. Ìåæäó àòîìàìè âîäîðîäà âîçíèêàþò êîíòàêòíûå ñâÿçè, ôîðìèðóþùèå ôðàêòàëüíûé êëàñòåð àòîìîâ âîäîðîäà, êîòîðûé îáðàçóåò âàíäåð-âààëüñîâñêèå ñâÿçè ñ ïîâåðõíîñòíûìè àòîìàìè óãëåðîäà ïîäëîæêè (ðèñ. 4).  ñèëó òîãî, ÷òî íå âîçíèêàåò êîíòàêòíîãî îáìåííîãî âçàèìîäåéñòâèÿ «àòîì â àòîì» ñ óãëåðîäíîé ïîäëîæêîé, îáðàçóåòñÿ áîëåå ïëîòíàÿ óïàêîâêà Í-àòîìîâ â ïîëèêîíäåíñàòå. Ñ öåëüþ ïîäòâåðæäåíèÿ âûäâèíóòîé íàìè ìîäåëè îáðàçîâàíèÿ ïîëèêîíäåíñàòà àòîìîâ âî- Ðèñ. 5. Ìîäåëüíûé ïîòåíöèàë ïîëèêîíäåíñàòà âîäîðîäà â ðàñ÷åòå íà ïàðó àòîìîâ Í–Í ïðè ó÷åòå òðåõ êîîðäèíàöèîííûõ ñôåð 8 Ìîäåëèðîâàíèå ñòðîåíèÿ ïîëèêîíäåíñàòîâ âîäîðîäà... ïîëèêîíäåíñàöèè (òðè êîîðäèíàöèîííûõ ñôåðû ó÷òåíû): ÅÍ–Í = 475 êÄæ/ìîëü, r0Í-Í = 0.086 íì. Ñðàâíèâàÿ èõ ñ ðàâíîâåñíûìè ïàðàìåòðàìè Í2 : ÅÍ2 = 462 êÄæ/ìîëü, r0Í2 = 0.075 íì, âèäíî, ÷òî â ýòîì ñëó÷àå âîçìîæíî îáðàçîâàíèå ïîëèêîíäåíñàòà ôèíèòíûõ àòîìîâ âîäîðîäà ñ âûäåëåíèåì 13 êÄæ/ìîëü òåïëà. Ýíåðãèÿ ñóïðàìîëåêóëÿðíîãî îáìåííîãî âçàèìîäåéñòâèÿ ñ óâåëè÷åíèåì ÷èñëà âîäîðîäíûõ àòîìîâ â êëàñòåðå óâåëè÷èâàåòñÿ, ïðè ýòîì äëèíà ñâÿçè óìåíüøàåòñÿ. Ïîýòîìó äîëæíî îáðàçîâàòüñÿ ïîëèêîíäåíñàòíîå ñîñòîÿíèå àòîìîâ âîäîðîäà ñ âûõîäîì âñåõ ðàâíîâåñíûõ ïàðàìåòðîâ íà íàñûùåíèå. Ïðîöåññ ïîëèêîíäåíñàöèè èìååò êðèòè÷åñêèé ðàçìåð êëàñòåðíîãî çàðîäûøà. Êî- ëè÷åñòâî àòîìîâ âîäîðîäà, ïðèõîäÿùååñÿ íà îäèí àòîì óãëåðîäà â ìîíîñëîå, óâåëè÷èâàåòñÿ çà ñ÷åò ýôôåêòà ñàìîóïëîòíåíèÿ êîíäåíñàòà. Ñ ðîñòîì ÷èñëà àòîìîâ âîäîðîäà óìåíüøàåòñÿ ìåæàòîìíîå ðàññòîÿíèå Í–Í è â ðåçóëüòàòå ýòîãî ïëîòíîñòü óêëàäêè àòîìîâ âîçðàñòàåò ñ 1 : 1 (õèìè÷åñêàÿ àäãåçèÿ íà óãëåðîä) äî 3.8 : 1 (ôèçè÷åñêàÿ àäãåçèÿ íà óãëåðîä). Ïðè çàïîëíåíèè ïîëîñòè íàíîóãëåðîäà âîäîðîäîì â ñîîòíîøåíèè 1: 1 ìàññîâàÿ äîëÿ âîäîðîäà ñîñòàâëÿåò ïîðÿäêà 8 âåñ. %.  ñëó÷àå ñîîòíîøåíèÿ 3.8 : 1 â íàíîñòðóêòóðå óãëåðîäà ìîæåò íàõîäèòüñÿ äî 30 âåñ. % àòîìîâ âîäîðîäà â ïîëèêîíäåíñàòå, êîòîðûé ôèçè÷åñêè àäñîðáèðîâàí íà ñòåíêàõ óãëåðîäà. Ëèòåðàòóðà 1. Óìýäçàâà Õ. Òåðìîïîëåâàÿ äèíàìèêà è êîíäåíñèðîâàííûå ñîñòîÿíèÿ / Õ. Óìýäçàâà, Õ. Ìàöóìîòî, Ì. Òàòèêè: Ïåð. ñ àíãë. Ì., 1985. 2. Áåçíîñþê Ñ.À. Ìíîãîóðîâíåâîå ñòðîåíèå, ôèçèêî-õèìè÷åñêèå è èíôîðìàöèîííûå ñâîéñòâà âåùåñòâà / Ñ.À. Áåçíîñþê, À.È. Ïîòåêàåâ, Ì.Ñ. Æóêîâñêèé, Ò.Ì. Æóêîâñêàÿ Ë.Â., Ôîìèíà. Òîìñê, 2005. 3. Drexler K.E. Nanosystems (Molecular Machinary, Manifacturing and Computation). New-York, 1992. 4. Beznosyuk S.A. Materials Science & Engineering C. / S.A. Beznosyuk, A.V. Kolesnikov, D.A. Mezentzev, M.S. Zhukovsky, T.M. Zhukovsky. 2002. V. 19. ¹1. 5. Beznosyuk S.A. Materials Science & Engineering C. 2002. V. 19. ¹1. 6. Zittel A. Materials Today. 2003. ¹9. 7. Beznosyuk S.A. Hydrogen materials science and chemistry of carbon nanomaterials / S.A. Beznosyuk, D.A. Mezentzev, M.S. Zhukovsky, T.M. Zhukovsky. // NATO Science Series: II Mathematics, Physics and Chemistry. 2004. V. 172. ¹1. 8. Beznosyuk S.A. Computational Materials Science / S.A. Beznosyuk, M.S. Beznosyuk, D.A. Mezentzev. 1999. V. 14. 9. Áåéäåð Ð. Àòîìû â ìîëåêóëàõ: Êâàíòîâàÿ òåîðèÿ: Ïåð. ñ àíãë. Ì., 2001. 9