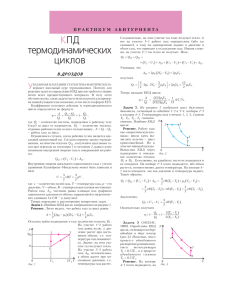
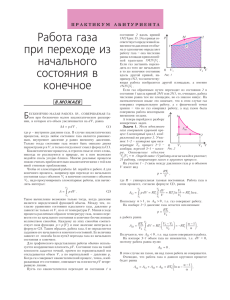
Отсюда получаем, что теплоемкость при постоянном давлении
реклама
50 ÊÂÀÍT 2000/¹3 Îòñþäà ïîëó÷àåì, ÷òî òåïëîåìêîñòü ïðè ïîñòîÿííîì äàâëåíèè ïîñòîÿííà è äëÿ îäíîãî ìîëÿ ãàçà ðàâíà Cp = CV + R = 5 2 R. η= Q1 = A Q1 . Ðàçáåðåì òåïåðü íåêîòîðûå êîíêðåòíûå çàäà÷è íà òåïëîâûå ïðîöåññû ñ ó÷àñòèåì îäíîàòîìíîãî èäåàëüíîãî ãàçà. Çàäà÷à 1. Ñðàâíèòå ðàáîòû, êîëè÷åñòâà òåïëîòû è òåïëîåìêîñòè 1 ìîëÿ èäåàëüíîãî ãàçà ïðè ïåðåõîäå ìåæäó äâóìÿ èçîòåðìàìè ñ òåìïåðàòóðàìè T1 è T2 â èçîáàðè÷åñêîì ïðî- p 1 D 3 2 ? D Q1 = ∆U1 + A = ? 5 D p R T2 − T1 . 2 Äëÿ ïðîöåññà 2 (íà äèàãðàììå pV ïðÿìàÿ ïðîõîäèò ÷åðåç íà÷àëî êîîðäèíàò) ðàáîòà ðàâíà ïëîùàäè çàøòðèõîâàííîé òðàïåöèè: A= p1 + p2 2 ?V − V D = 2 1 p2V2 − p1V1 = 2 ?T 2 R 2 D − T1 . Èçìåíåíèå âíóòðåííåé ýíåðãèè â ýòîì ïðîöåññå òàêîå æå, êàê â ïðåäûäóùåì: ∆U2 = ∆U1 = > C 3 R T2 − T1 , 2 à êîëè÷åñòâî òåïëîòû, ïîäâåäåííîå íà ó÷àñòêå 2, ðàâíî ? D Q2 = A2 + ∆U2 = 2 R T2 − T1 . Êàê âèäíî, â îáîèõ ïðîöåññàõ ðàáîòà è ïîäâåäåííîå êîëè÷åñòâî òåïëîòû îïðåäåëÿþòñÿ ëèøü ðàçíîñòüþ òåìïåðàòóð êîíå÷íîãî è íà÷àëüíîãî ñîñòîÿíèé ãàçà. Ñëåäîâàòåëüíî, òåïëîåìêîñòè â ïðîöåññàõ îñòàþòñÿ ïîñòîÿííûìè è ðàâíûìè, ñîîòâåòñòâåííî, C1 = 5 2 R , C2 = 2 R . Ïðè ýòîì, íåçàâèñèìî îò íà÷àëüíîãî äàâëåíèÿ äëÿ èçîáàðû è îò íàêëîíà ïðÿìîé â ïåðåõîäå ñ ïðÿìîé ïðîïîðöèîíàëüíîé çàâèñèìîñòüþ äàâëåíèÿ îò îáúåìà, ðàáîòû ïåðåõîäà ìåæäó äâóìÿ èçîòåðìàìè îòëè÷àþòñÿ â 2 ðàçà, à òåïëîåìêîñòè â 5/4 ðàçà. Çàäà÷à 2. Ñðàâíèòå ðàáîòû è êîëè÷åñòâà òåïëîòû, ïîäâåäåííûå ê 1 ìîëþ ãàçà, â ïðîöåññå 1 èçîòåðìè÷åñêîãî ðàñøèðåíèÿ ãàçà îò îáúåìà V1 äî V2 è â ïðîöåññå 2 ïåðåõîäà ìåæäó ýòèìè ñîñòîÿíèÿìè ñ ëèíåéíîé çàâèñèìîñòüþ äàâëåíèÿ îò îáúåìà (ðèñ.2). Äëÿ ïðîöåññà 1 èìååì: V2 V1 , Q1 = A1 . 2 Äëÿ ïðîöåññà 2 ðàáîòà ðàâíà ïëîùàäè ñîîòâåòñòâóþùåé òðàïåöèè: Ò V V 2 1 R T2 − T1 , A1 = RT ln Ò Ðèñ. 1 ∆U1 = = Åùå ðàç ïîä÷åðêíåì, ÷òî äëÿ íàõîæäåíèÿ ïðàâèëüíîãî çíà÷åíèÿ ÊÏÄ íåîáõîäèìî ïîäñ÷èòàòü òåïëî, ïîäâåäåííîå íà âñåõ ó÷àñòêàõ ïðîöåññîâ, ñîñòàâëÿþùèõ öèêë. Òàê íàïðèìåð, â èçîõîðè÷åñêèõ ïðîöåññàõ ðàáîòà ãàçîì íå ïðîèçâîäèòñÿ, îäíàêî òåïëî ïîäâîäèòñÿ èëè îòâîäèòñÿ.  çàäà÷àõ ìîãóò òàêæå âñòðå÷àòüñÿ âíåøíå ïðîñòûå ó÷àñòêè çàâèñèìîñòè ð(V), â õîäå êîòîðûõ òåïëî êàê îòâîäèòñÿ, òàê è ïîäâîäèòñÿ. Åñëè äëÿ òàêîãî ó÷àñòêà íàéòè «èòîãîâîå» ïîäâåäåííîå èëè îòâåäåííîå òåïëî, òî ïðè ïîäñ÷åòå ÊÏÄ ìîæåò âîçíèêíóòü îøèáêà. Îòìåòèì, íàêîíåö, ÷òî òîëüêî äëÿ öèêëà Êàðíî, ñîñòîÿùåãî èç äâóõ èçîòåðì ñ òåìïåðàòóðàìè íàãðåâàòåëÿ T1 è õîëîäèëüíèêà T2 , íà êîòîðûõ, ñîîòâåòñòâåííî, ïîäâîäèòñÿ êîëè÷åñòâî òåïëîòû Q1 è îòâîäèòñÿ Q2 , è äâóõ àäèàáàò, ÊÏÄ ìîæåò áûòü çàïèñàí â âèäå Q − Q2 T − T2 η= 1 = 1 . Q1 T1 p p ? p p A1 = R T2 − T1 , Íàïîìíèì òàêæå îïðåäåëåíèå ÊÏÄ òåïëîâîé ìàøèíû, ðàáîòàþùåé ïî çàìêíóòîìó öèêëó, â ðåçóëüòàòû êîòîðîãî âíóòðåííÿÿ ýíåðãèÿ ãàçà (ðàáî÷åãî òåëà) íå èçìåíÿåòñÿ. Ïî çàêîíó ñîõðàíåíèÿ ýíåðãèè, ðàáîòà ãàçà â çàìêíóòîì öèêëå À ðàâíà ðàçíîñòè êîëè÷åñòâà òåïëîòû Q1 , ïîäâåäåííîãî ê ãàçó, è êîëè÷åñòâà òåïëîòû Q2 , îòâåäåííîãî îò íåãî. ÊÏÄ öèêëà íàçûâàåòñÿ îòíîøåíèå Q1 − Q2 öåññå 1 è â ïðîöåññå 2 ñ ïðÿìîé ïðîïîðöèîíàëüíîé çàâèñèìîñòüþ äàâëåíèÿ îò îáúåìà (ðèñ.1). Äëÿ èçîáàðû 1 ìû èìååì: V A2 = p1 + p2 2 ?V − V D , 2 1 V V V Ðèñ. 2 èëè, åñëè ââåñòè îáîçíà÷åíèå V2 V1 = = α è âîñïîëüçîâàòüñÿ óðàâíåíèåì èçîòåðìû p1V1 = p2V2 = RT, A2 = p1V2 − p2V1 2 = RT 2 α −1 2α . Âíóòðåííÿÿ ýíåðãèÿ â ïðîöåññå 2, êàê è â ïðîöåññå 1, íå èçìåíèëàñü, ïîýòîìó ïî çàêîíó ñîõðàíåíèÿ ýíåðãèè ìîæíî óòâåðæäàòü, ÷òî ãàçó áûëî ïåðåäàíî êîëè÷åñòâî òåïëîòû Q2 = A2 . Èòàê, äëÿ îáîèõ ïðîöåññîâ ðàáîòà îïðåäåëÿåòñÿ îòíîøåíèåì êîíå÷íîãî è íà÷àëüíîãî îáúåìîâ. Îòìåòèì, ÷òî äëÿ ïðîöåññà 2 òåïëîåìêîñòü íå îñòàåòñÿ ïîñòîÿííîé, áîëåå òîãî îíà ìåíÿåò çíàê â õîäå ïðîöåññà îò ïîëîæèòåëüíîãî ê îòðèöàòåëüíîìó. Ýòî îçíà÷àåò, ÷òî ñíà÷àëà òåïëî ïîäâîäèòñÿ, à çàòåì îòâîäèòñÿ. Çàäà÷à 3. Âåðøèíû çàìêíóòîãî öèêëà, ñîñòîÿùåãî èç ÷åòûðåõ ó÷àñòêîâ ëèíåéíîé çàâèñèìîñòè äàâëåíèÿ îò îáúåìà, ëåæàò íà äâóõ èçîòåðìàõ ñ èçâåñòíûìè òåìïåðàòóðàìè T1 è T2 p 2 1 3 " Ðèñ. 3 Ò Ò V (ðèñ.3). Ïðÿìûå 12 è 34 ïðîõîäÿò ÷åðåç íà÷àëî êîîðäèíàò, îáúåìû V2 è V4 ðàâíû. Íàéäèòå ðàáîòó îäíîãî ìîëÿ ãàçà â çàìêíóòîì öèêëå. Ðàáîòû íà ó÷àñòêàõ 12 è 34 îäèíàêîâû ïî âåëè÷èíå (ñì., íàïðèìåð, çàäà÷ó 1). Ïîýòîìó ðàáîòà â öèêëå ðàâíà A = A23 − A41 .