К теории взрывных волн от горючих облаков
реклама

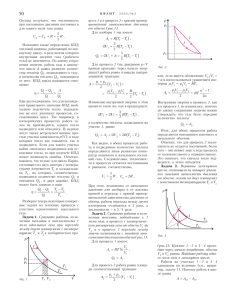
Ê òåîðèè âçðûâíûõ âîëí îò ãîðþ÷èõ îáëàêîâ Àñëàíîâ Ñ.Ê., Øêóëèïà Ñ.À., Öàðåíêî À.Ï. Îäåññêèé Ãîñóäàðñòâåííûé Óíèâåðñèòåò, Îäåññà 270026, óë. Äâîðÿíñêàÿ ä. 2 Ïðè ðàññìîòðåíèè âçðûâà ãàçîâîãî îáëàêà â îêðóæàþùåé àòìîñôåðå îäíèì èç ãëàâíûõ ïàðàìåòðîâ ðàçâèâàþùåãîñÿ òå÷åíèÿ ñëóæèò ïåðåïàä äàâëåíèÿ âî ôðîíòå âîçíèêàþùåé óäàðíîé âîëíû (ÓÂ): ∆Ð = (Ð1 - Ð0) / Ð0 , ãäå Ð0 è Ð1 äàâëåíèå ïåðåä è çà åå ôðîíòîì ñîîòâåòñòâåííî. Ïîñêîëüêó äàííîå ÿâëåíèå îáëàäàåò âåñüìà ñëîæíîé ñòðóêòóðîé, òî ïðè åãî ìîäåëèðîâàíèè îñóùåñòâëÿþòñÿ ñëåäóþùèå äîïóùåíèÿ: ñôåðè÷åñêîå îáëàêî ðàäèóñà r0 ìãíîâåííî ïðîäåòîíèðîâàâøåé ãàçîâîé ñìåñè ñîäåðæèò ïðîäóêòû âçðûâà ýíåðãèè Å0, ÷åìó ñòàâèòüñÿ â ñîîòâåòñòâèå ðàâíîìåðíîå ðàñïðåäåëåíèå äàâëåíèÿ Ð1 ïî âñåìó îáúåìó; ïîêàçàòåëü àäèàáàòû ïðîäóêòîâ γ 1 . Èõ ðàçëåò ïðîèñõîäèò ñôåðè÷åñêè ñèììåòðè÷íî â îäíîðîäíóþ îêðóæàþùóþ àòìîñôåðó ñ äàâëåíèåì Ð0 è ïîêàçàòåëåì àäèàáàòû γ0.  äàííîé ðàáîòå îñóùåñòâëÿåòñÿ ïîïûòêà àíàëèòè÷åñêîãî ïîñòðîåíèÿ çàâèñèìîñòè ∆Ð(R), åäèíîîáðàçíîé, äëÿ âñåãî r ∈ (r 0 ,∞) èíòåðâàëà r ðàñïðîñòðàíåíèÿ ñôåðè÷åñêîé óäàðíîé âîëíû (ÓÂ); R = (E / P )1 / 3 0 0 áåçðàçìåðíàÿ êîîðäèíàòà ôðîíòà ÓÂ. Êàê ïîêàçàíî â [9], âçðûâ çàðÿäà êîíå÷íîãî îáúåìà (ÂÇÊÎ) ñ ýíåðãèåé Å0 íà áîëüøèõ ðàññòîÿíèÿõ îò ìåñòà ñâîåãî âîçíèêíîâåíèÿ ýêâèâàëåíòåí òî÷å÷íîìó âçðûâó (ÒÂ) ñ ýíåðãèåé ηÅ0. Èç ñîâïàäåíèÿ äåéñòâèÿ ýòèõ âçðûâîâ â äàëüíåé çîíå ñëåäóåò, ÷òî ãëàâíûå ÷ëåíû äëÿ ïðåäñòàâëåíèé ∆Ð äîëæíû ñîâïàäàòü ïðè R→∞ ñ ó÷åòîì ïðèìåíÿåìîãî êîýôôèöèåíòà ýíåðãåòè÷åñêîãî ïîäîáèÿ η: ∆ÐÂÊÎ(R) R→∞ = ∆ÐÒÂ(Rη-1/3)R→∞ . Âåëè÷èíà η âûðàæåíà â Ð 1 /Ð 0 , γ , γ 1 . Ïîýòîìó íèæå ðàññìàòðèâàåòñÿ â êà÷åñòâå [10] ÷åðåç âñïîìîãàòåëüíîãî òî÷å÷íûé âçðûâ è äëÿ íåãî îòäåëüíî ñòðîèòñÿ âûðàæåíèå ∆Ð(R), ïî êîòîðîìó óäàåòñÿ, â ñâîþ î÷åðåäü, ïîñòðîèòü ñîîòâåòñòâóþùåå âûðàæåíèå äëÿ ÂÇÊÎ. Àíàëèòè÷åñêîå ïîñòðîåíèå åäèíîé ôîðìóëû ïåðåïàäà äàâëåíèÿ ∆Ð(R) íà âñåì ïðîìåæóòêå (0, ∞ ) ðàñïðîñòðàíåíèÿ ñôåðè÷åñêîé óäàðíîé âîëíû, îáðàçîâàííîé ÒÂ, ïðîèçâîäèòñÿ ìåòîäîì ñðàùèâàíèÿ àñèìïòîòè÷åñêèõ ðàçëîæåíèé [5] íà êîíöàõ ðàññìàòðèâàåìîãî èíòåðâàëà. Ðåøåíèå àâòîìîäåëüíîé çàäà÷è î ñèëüíîì âçðûâå, îïèñûâàþùåå ÿâëåíèå íà íà÷àëüíîé ñòàäèè ðàñïðîñòðàíåíèÿ óäàðíîé âîëíû, êîãäà äàâëåíèåì â îêðóæàþùåì ãàçå ìîæíî ïðåíåáðå÷ü ïî ñðàâíåíèþ ñ òàêîâûì íà ôðîíòå ÓÂ, 124 ïîëó÷åíî â [1]. Âûðàæåíèå äëÿ ïåðåïàäà äàâëåíèÿ âî ôðîíòå Ó èìååò ñëåäóþùèé áåçðàçìåðíûé âèä: ∆Ρ(R ) = 8α 25( γ + 1) R 3 , (1) ãäå γ ïîêàçàòåëü àäèàáàòû, α = α(γ) îïðåäåëåííûé êîýôôèöèåíò. Ñîãëàñíî [6], [7] àñèìïòîòè÷åñêîå ïðåäñòàâëåíèå ïåðåïàäà äàâëåíèÿ â ñôåðè÷åñêîé óäàðíîé âîëíå âäàëè îò ìåñòà åå âîçíèêíîâåíèÿ âûãëÿäèò ñëåäóþùèì îáðàçîì: , (2) ãäå À1, À2,  íåèçâåñòíûå êîýôôèöèåíòû, ïîäëåæàùèå îïðåäåëåíèþ. Ïðåäñòàâèì èñêîìóþ ôóíêöèþ ∆Ð(R) â âèäå: . (3) Ïîñëåäíèé ïðè R→∞ ñîãëàñóåòñÿ ñ âûðàæåíèåì (2), ÷òî ëåãêî ïîêàçàòü, ëèíåàðèçóÿ âõîäÿùèå ôóíêöèè. Íåèçâåñòíûå êîýôôèöèåíòû B, A1, A2, A3, C1, C2 îïðåäåëÿþòñÿ íà÷àëüíîé êîíôèãóðàöèåé ÓÂ, êîòîðàÿ çàäàåòñÿ èñòî÷íèêîì. Çíà÷èò, äëÿ èõ íàõîæäåíèÿ ñëåäóåò ðàññìîòðåòü êàê äàëüíþþ, òàê è áëèæíþþ çîíû âçðûâà. Íå òðóäíî óáåäèòüñÿ â òîì, ÷òî ñðàñòèòü (3) ñ (1) ïðè R → 0 ïðåäñòàâëÿåòñÿ âîçìîæíûì òîëüêî ïðè óñëîâèè Ñ2 =1. Âûðàæåíèå ∆Ð(R), çàïèñàííîå â âèäå (4), ÿâëÿåòñÿ îêîí÷àòåëüíûì äëÿ ïåðåïàäà äàâëåíèÿ âî ôðîíòå óäàðíîé âîëíû. Îíî óäîâëåòâîðÿåò è ðåøåíèþ [1], êîòîðîå ÿâëÿåòñÿ àñèìïòîòè÷åñêèì äëÿ âçðûâà ñ ïðîòèâîäàâëåíèåì, è àñèìïòîòèêå [7]. Ñðàùèâàíèå âûðàæåíèé (3) è (1) ïðîâåäåì äëÿ ÷ëåíîâ ïîðÿäêà R-3 è R-2, ó÷èòûâàÿ, ÷òî ïîïðàâî÷íûì ñëàãàåìûì ê (1), ñîãëàñíî [2], áóäåò ÷ëåí Î(1). Êðîìå òîãî, âîñïîëüçóåìñÿ çàêîíîì ñîõðàíåíèÿ ýíåðãèè â âèäå èíòåãðàëà ýíòðîïèéíûõ ïîòåðü, íàéäåííîãî â [9]: . (4)  ðåçóëüòàòå èìååì òðè óñëîâèÿ äëÿ ïÿòè íåèçâåñòíûõ âåëè÷èí A1, A2, A3, B, C1, òàê ÷òî äâà êîýôôèöèåíòà îñòàþòñÿ â êà÷åñòâå ïîäãîíî÷íûõ. È îïðåäåëÿþòñÿ èç óñëîâèÿ íàèëó÷øåãî ðàâíîìåðíîãî ïðèáëèæåíèÿ ê èçâåñòíûì ÷èñëåííûì ðåøåíèÿì [3], [4]. Ìåòîä íàèìåíüøèõ êâàäðàòîâ â äàííîì ñëó÷àå íå ýôôåêòèâåí, ïîñêîëüêó ôóíêöèÿ ∆Ð(R) èçìåíÿåòñÿ â áåñêîíå÷íûõ ïðåäåëàõ è íà áåñêîíå÷íîì èíòåðâàëå. Äëÿ âû÷èñëåíèÿ èíòåãðàëà â óðàâíåíèè (4) âîñïîëüçóåìñÿ 125 àñèìïòîòè÷åñêèì ïðåäñòàâëåíèåì ïîäûíòåãðàëüíîé ôóíêöèè íà êîíöàõ èíòåðâàëà èíòåãðèðîâàíèÿ. Èñïîëüçóÿ äàííûå ðàñ÷åòîâ [3], [4] (ïðè γ = 1.4 , α = 0.851 , Ð0 = 1àòì) ïðèõîäèì ê ñëåäóþùèì çíà÷åíèÿì íåèçâåñòíûõ ïàðàìåòðîâ: A1 = 0.28, A2 = 0.054, A3 = -0.092, B = 1.7, C = 1.5; ðàñõîæäåíèå ñ ðåçóëüòàòàìè ÷èñëåííîãî ñ÷åòà íå ïðåâîñõîäèò 5.5%. Òàêèì îáðàçîì, ãëàâíûé ÷ëåí âûðàæåíèÿ ∆Ð(R) äëÿ ÂÇÊÎ ñëåäóåò èñêàòü â âèäå: ∆P(R ) = 0.28 −1 / 3 Rη−1 / 3 ln Rη B + C , ãäå íåèçâåñòíûå êîýôôèöèåíòû  è Ñ íàõîäÿòñÿ èç óñëîâèÿ íà÷àëüíîãî ðàñïàäà íà ïîâåðõíîñòè ñôåðû ∆Ð(R0) è çàêîíà ñîõðàíåíèÿ ýíåðãèè â âèäå èíòåãðàëà ýíòðîïèéíûõ ïîòåðü äëÿ ÂÇÊÎ, ïîëó÷åííîãî â [9]: êîòîðûå îáðàçóþò çàìêíóòóþ ñèñòåìó óðàâíåíèé. Ðàññ÷èòàííûå êîýôôèöèåíòû ïîçâîëÿþò ïîñòðîèòü íà âñåì èíòåðâàëå ðàñïðîñòðàíåíèÿ âçðûâíîé âîëíû åäèíóþ ôîðìóëó äëÿ âû÷èñëåíèÿ ïåðåïàäà äàâëåíèÿ âî ôðîíòå ÓÂ, êîòîðàÿ äàåò õîðîøåå ñîâïàäåíèå ñ ýêñïåðèìåíòàëüíûìè ðåçóëüòàòàìè ïî âçðûâó ãàçîâûõ îáëàêîâ [10]; ðàñõîæäåíèÿ ñ ýêñïåðèìåíòàëüíûìè èçìåðåíèÿìè ñîñòàâëÿþò 30%. Íà ïðèâåäåííîì â ëîãàðèôìè÷åñêîì ìàñøòàáå ãðàôèêå êðåñòèêàìè îáîçíà÷åíû ýêñïåðèìåíòàëüíûå çíà÷åíèÿ, ïîëó÷åííûå â [10] äëÿ ðàçëåòà ïðîäóêòîâ âçðûâà ñìåñè C2H2+2.5O2+9.4N2 , íåïðåðûâíàÿ êðèâàÿ ýòî ∆P(R) 100 11.2 10 1 0.1 0.01 0.1 0.18 1 126 10 çíà÷åíèÿ âû÷èñëåííûå ïðåäëîæåííûì âûøå ìåòîäîì (íà÷àëüíûé ðàäèóñ 0.179R, íà÷àëüíàÿ èíòåíñèâíîñòü óäàðíîé âîëíû â âîçäóõå ïðè ðàñïàäå äåòîíàöèîííîé âîëíû íà ãðàíèöå âçðûâ÷àòîé ãàçîâîé ñìåñè ñ âîçäóõîì 11.2 àòì, âíåøíåå äàâëåíèå 1àòì, ïîêàçàòåëè àäèàáàò ïðîäóêòîâ âçðûâà γ1 = 1.38, îêðóæàþùåé ñðåäû γ = 1.4 ). 1. Ñåäîâ Ë.È. Ðàñïðîñòðàíåíèå ñèëüíûõ âçðûâíûõ âîëí. // Ïðèêëàäíàÿ ìàòåìàòèêà è ìåõàíèêà. 1946. T. 10. âûï. 2. Ñ. 156-164; 2. Ìåëüíèêîâà Í.Ñ. Èññëåäîâàíèå çàäà÷è î òî÷å÷íîì âçðûâå. // Äèññåðòàöèÿ. Ìîñêâà. 1953. 173 ñ.; 3. Îõîöèìñêèé Ä.Å., Êîíäðàøåâà È.Ë., Âëàñîâà Ç.Ï., Êîçàêîâà Ð.Ê. Ðàñ÷åò òî÷å÷íîãî âçðûâà ñ ó÷åòîì ïðîòèâîäàâëåíèÿ. // Òðóäû Ìàòåìàòè÷åñêîãî èíñòèòóòà ÀÍ ÑÑÑÐ. 1957. T. 50. 156 ñ.; 4. Îõîöèìñêèé Ä.Å. Âëàñîâà Ç.Ï. Î ïîâåäåíèè óäàðíîé âîëíû íà áîëüøèõ ðàññòîÿíèÿõ îò öåíòðà âçðûâà. // Æóðíàë âû÷. ìàò è ìàò. Ôèçèêè. 1962. T. 2. ¹1. Ñ. 107 124. 5. Ìèëòîí Âàí Äàéê. // Ìåòîäû ñðàùèâàíèÿ â ãàçîâîé äèíàìèêå. Ìèð 1967. 6. Ëàíäàó Ë.Ä. Îá óäàðíûõ âîëíàõ íà äàëåêèõ ðàññòîÿíèÿõ îò ìåñòà èõ âîçíèêíîâåíèÿ. // Ïðèêëàäíàÿ ìàòåìàòèêà è ìåõàíèêà. 1945. T. 9. Âûï. ¹4. Ñ. 96-103. 7. ßêèìîâ Þ.Ë. Îá àñèìïòîòè÷åñêèõ ðåøåíèÿõ óðàâíåíèé îäíîìåðíîãî íåóñòàíîâèâøåãîñÿ äâèæåíèÿ èäåàëüíîãî ãàçà è îá àñèìïòîòè÷åñêèõ çàêîíàõ çàòóõàíèÿ óäàðíûõ âîëí.// Ïðèêëàäíàÿ ìàòåìàòèêà è ìåõàíèêà. 1955. T. 19. Âûï. ¹6. Ñ. 681 692. 8. Ãóáêèí Ê.È. // Ìåõàíèêà â ÑÑÑÐ çà 50 ëåò. Ìîñêâà. Íàóêà. 1967. Ñ. 456; 9. Àñëàíîâ Ñ.Ê. Ãîëèíñêèé Î.Ñ. Ýíåðãèÿ Àñèìïòîòè÷åñêè ýêâèâàëåíòíîãî òî÷å÷íîãî âçðûâà äëÿ çàðÿäà êîíå÷íîãî îáúåìà // Æóðíàë ïðèêëàäíîé ìåõàíèêè è òåõíè÷åñêîé ôèçèêè. 1988. ¹6. Ñ. 44 51. 10. Êîãàðêî Ñ.Ì. Àäóøêèí Â.Â. Ëÿìèí À.Ã. Èññëåäîâàíèå ñôåðè÷åñêîé äåòîíàöèè ãàçîâûõ ñìåñåé // Íàó÷íî-òåõíè÷åñêèå ïðîáëåìû ãîðåíèÿ è âçðûâà. 1965. ¹2. Ñ. 22 34. 127