15. Работа газа при переходе из начального состояния в

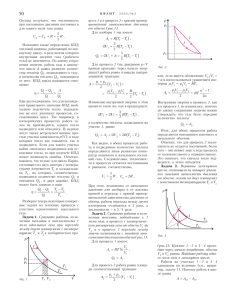
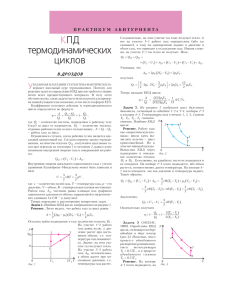
ÏÐÀÊÒÈÊÓÌ ÀÁÈÒÓÐÈÅÍÒÀ
Ðàáîòà ãàçà
ïðè ïåðåõîäå èç
íà÷àëüíîãî
ñîñòîÿíèÿ â
êîíå÷íîå
Â.ÌÎÆÀÅÂ
Á
ÅÑÊÎÍÅ×ÍÎ ÌÀËÀß ÐÀÁÎÒÀ δA , ÑÎÂÅÐØÀÅÌÀß ÃÀ-
çîì ïðè áåñêîíå÷íî ìàëîì êâàçèñòàòè÷åñêîì ðàñøèðåíèè, â êîòîðîì åãî îáúåì óâåëè÷èâàåòñÿ íà dV, ðàâíà
δA = p dV ,
(1)
ãäå ð – âíóòðåííå äàâëåíèå ãàçà.  ñëó÷àå êâàçèñòàòè÷åñêèõ
ïðîöåññîâ, êîãäà ëþáîå ñîñòîÿíèå ãàçà ÿâëÿåòñÿ ðàâíîâåñíûì, âíóòðåííåå äàâëåíèå ð ðàâíî âíåøíåìó äàâëåíèþ.
Òîëüêî òîãäà ñîñòîÿíèå ãàçà ìîæåò áûòü îïèñàíî äâóìÿ
ïàðàìåòðàìè ð è V, è òîëüêî òîãäà èìååò ñìûñë ôîðìóëà (1).
Êâàçèñòàòè÷åñêèå ïðîöåññû, â ñòðîãîì ñìûñëå ýòîãî ñëîâà,
íèêîãäà íå ðåàëèçóþòñÿ â ïðèðîäå, íî ê íèì âîçìîæíî
ïîäîéòè ñêîëü óãîäíî áëèçêî. Ìíîãèå ðåàëüíûå ïðîöåññû
ìîæíî ñ÷èòàòü ïðèáëèçèòåëüíî êâàçèñòàòè÷åñêèìè ñ òîé èëè
èíîé ñòåïåíüþ ïðèáëèæåíèÿ.
×òîáû îò ýëåìåíòàðíîé ðàáîòû δA ïåðåéòè ê ðàáîòå A äëÿ
êîíå÷íîãî ïðîöåññà, íàïðèìåð ïðè ïåðåõîäå èç íà÷àëüíîãî
ñîñòîÿíèÿ ãàçà ñ îáúåìîì V1 â êîíå÷íîå ñîñòîÿíèå ñ îáúåìîì
V2 , íàäî ïðîñóììèðîâàòü ýëåìåíòàðíûå ðàáîòû, èëè âû÷èñëèòü èíòåãðàë:
A=
V2
ò p dV .
V1
(2)
Òàêîå âû÷èñëåíèå âîçìîæíî òîëüêî òîãäà, êîãäà äàâëåíèå
ÿâëÿåòñÿ îïðåäåëåííîé ôóíêöèåé îáúåìà. Ìåæäó òåì, ñîãëàñíî óðàâíåíèþ ñîñòîÿíèÿ èäåàëüíîãî ãàçà, äàâëåíèå ð
çàâèñèò íå òîëüêî îò V, íî è îò òåìïåðàòóðû Ò. Ìåíÿÿ â õîäå
ïðîöåññà ðàçëè÷íûì îáðàçîì òåìïåðàòóðó ãàçà, ìîæíî ïåðåâåñòè åãî èç íà÷àëüíîãî ñîñòîÿíèÿ â êîíå÷íîå áåñ÷èñëåííûì
êîëè÷åñòâîì ñïîñîáîâ. Êàæäîìó èç ýòèõ ñïîñîáîâ ñîîòâåòñòâóåò ñâîÿ ôóíêöèÿ p = p V è ñâîå çíà÷åíèå èíòåãðàëà â
ôîðìóëå (2). Òàêèì îáðàçîì, ðàáîòà ãàçà À íå îïðåäåëÿåòñÿ
çàäàíèåì åãî íà÷àëüíîãî è êîíå÷íîãî ñîñòîÿíèé. Åå âåëè÷èíà
çàâèñèò îò ñïîñîáà (èëè ïóòè) ïåðåõîäà ãàçà èç íà÷àëüíîãî
ñîñòîÿíèÿ â êîíå÷íîå.
Äëÿ ãðàôè÷åñêîãî ïðåäñòàâëåíèÿ ðàáîòû îáû÷íî èñïîëüçóåòñÿ êîîðäèíàòíàÿ ïëîñêîñòü pV. Ñîñòîÿíèå ãàçà íà òàêîé
ïëîñêîñòè çàäàåòñÿ òî÷êîé, ïðè÷åì ïî ãîðèçîíòàëüíîé îñè
îòêëàäûâàåòñÿ îáúåì V, à ïî âåðòèêàëüíîé – äàâëåíèå ð.
Êîãäà ãàç ñîâåðøàåò êâàçèñòàòè÷åñêèé ïðîöåññ, òî÷êà, èçîáðàæàþùàÿ åãî ñîñòîÿíèå, îïèñûâàåò íà ïëîñêîñòè pV íåïðåðûâíóþ ëèíèþ.
Ïóñòü ãàç êâàçèñòàòè÷åñêè ïåðåõîäèò èç ñîñòîÿíèÿ 1 â
ñîñòîÿíèå 2 âäîëü êðèâîé
1Ì2 (ðèñ.1). Ýòà êðèâàÿ ñîîòâåòñòâóåò îïðåäåëåííîé çàâèñèìîñòè äàâëåíèÿ îò îáúåìà è îäíîçíà÷íî îïðåäåëÿåò
ðàáîòó ãàçà – îíà ÷èñëåííî
ðàâíà ïëîùàäè êðèâîëèíåéíîé òðàïåöèè 1M2V2V1 .
Åñëè ãàç çàñòàâèòü ïåðåõîäèòü èç òîãî æå íà÷àëüíîãî
â òî æå êîíå÷íîå ñîñòîÿíèå
âäîëü äðóãîé êðèâîé, íà- Ðèñ. 1
ïðèìåð 1N2, òî ñîîòâåòñòâóþùàÿ ðàáîòà èçîáðàçèòñÿ äðóãîé ïëîùàäüþ, à èìåííî
1N2V2V1 .
Åñëè ãàç îáðàòèìûì ïóòåì ïåðåõîäèò èç ñîñòîÿíèÿ 2 â
ñîñòîÿíèå 1 âäîëü êðèâîé 2Ì1 èëè 2N1, òî, î÷åâèäíî, ðàáîòà
÷èñëåííî ðàâíà òåì æå ïëîùàäÿì, íî ñî çíàêîì ìèíóñ. Íà
ìàòåìàòè÷åñêîì ÿçûêå ýòî îçíà÷àåò, ÷òî â ýòîì ñëó÷àå ãàç
ñîâåðøèë îòðèöàòåëüíóþ ðàáîòó, à ñ ôèçè÷åñêîé òî÷êè
çðåíèÿ – ÷òî íå ãàç ñîâåðøèë ðàáîòó, à íàä ãàçîì áûëà
ñîâåðøåíà ðàáîòà íåêîòîðûìè
âíåøíèìè ñèëàìè.
À òåïåðü ïåðåéäåì ê ðàçáîðó
êîíêðåòíûõ çàäà÷.
Çàäà÷à 1. Ìîëü èäåàëüíîãî
ãàçà ñîâåðøàåò êðóãîâîé ïðîöåññ (çàìêíóòûé öèêë), èçîáðàæåííûé íà ðèñóíêå 2. Ó÷àñòîê 1–2 – èçîòåðìà ïðè òåìïåðàòóðå T1 , ïðîöåññ 2–3 –
èçîáàðà, ïåðåõîä 3–1 – èçîõî- Ðèñ. 2
ðà. Îòíîøåíèå îáúåìîâ
V2 V1 = α . Îïðåäåëèòå: 1) ðàáîòó ãàçà íà êàæäîì ó÷àñòêå;
2) ðàáîòó, ñîâåðøåííóþ ãàçîì â êðóãîâîì ïðîöåññå.
Íà ó÷àñòêå 1—2 ñâÿçü ìåæäó äàâëåíèåì ãàçà ð è îáúåìîì
V èìååò âèä
RT1
p=
,
V
ãäå R – óíèâåðñàëüíàÿ ãàçîâàÿ ïîñòîÿííàÿ. Ðàáîòà ãàçà â
ýòîì ïðîöåññå, ñîãëàñíî ôîðìóëå (2), ðàâíà
A12 =
V2
ò
V1
V2
p dV = RT1 ò
V1
V
dV
= RT1 ln 2 = RT1 ln α .
V
V1
Ïîñêîëüêó α > 1 , òî A12 > 0 , ò.å. ãàç ñîâåðøàåò ðàáîòó.
Íà èçîáàðå 2–3 äàâëåíèå ãàçà îñòàåòñÿ íåèçìåííûì:
RT1
,
p=
V2
à ðàáîòà ðàâíà
V
A23 =
æ V - V2 ö
RT1 2
æ α - 1ö
= - RT1 ç
dV = RT1 ç 1
.
è α ÷ø
V2 Vò
è V2 ÷ø
1
Ïîëó÷àåòñÿ, ÷òî A23 < 0 , ò.å. íàä ãàçîì ñîâåðøàåòñÿ ðàáîòà.
Íà èçîõîðå 3–1 îáúåì ãàçà íå èçìåíÿåòñÿ, ò.å. dV = 0,
ïîýòîìó ðàáîòà ðàâíà íóëþ:
A31 = 0 .
 ýòîì ñëó÷àå íè ãàçîì, íè íàä ãàçîì ðàáîòà íå ñîâåðøàåòñÿ.
Î÷åâèäíî, ÷òî ðàáîòà ãàçà â äàííîì êðóãîâîì ïðîöåññå
áóäåò ðàâíà
α - 1ö
æ
Aêð = A12 + A23 + A31 = RT1 ç ln α ÷.
è
α ø
""
ÊÂÀÍT 2007/¹3
Íà ðèñóíêå 2 ýòà ðàáîòà ÷èñëåííî ðàâíà ïëîùàäè âûäåëåííîé ôèãóðû 1–2–3.
Çàäà÷à 2. Ìîëü ãåëèÿ ðàñøèðÿåòñÿ èç íà÷àëüíîãî ñîñòîÿíèÿ 1 äî êîíå÷íîãî ñîñòîÿíèÿ 3 â äâóõ ïðîöåññàõ (ðèñ.3).
Ñíà÷àëà ðàñøèðåíèå èäåò â ïðîöåññå 1–2 ñ ïîñòîÿííîé òåïëîåì3
êîñòüþ C = R (R – óíèâåð4
ñàëüíàÿ ãàçîâàÿ ïîñòîÿííàÿ).
Çàòåì ãàç ðàñøèðÿåòñÿ â ïðîöåññå 2–3, êîãäà åãî äàâëåíèå ð
ïðÿìî ïðîïîðöèîíàëüíî îáúåìó
V. Íàéäèòå ðàáîòó, ñîâåðøåííóþ ãàçîì â ïðîöåññå 1–2, åñëè â
Ðèñ. 3
ïðîöåññå 2–3 îí ñîâåðøèë ðàáîòó À. Òåìïåðàòóðû íà÷àëüíîãî
(1) è êîíå÷íîãî (3) ñîñòîÿíèé ðàâíû.
Ïîñêîëüêó òåìïåðàòóðû ãàçà â íà÷àëüíîì è êîíå÷íîì
ñîñòîÿíèÿõ îäèíàêîâû, ïåðåõîä èç ñîñòîÿíèÿ 1 â ñîñòîÿíèå
3 ïðîèñõîäèò ñ ñîõðàíåíèåì âíóòðåííåé ýíåðãèè ãàçà. Ïî
ïåðâîìó íà÷àëó òåðìîäèíàìèêè, â ýòîì ñëó÷àå ñóììàðíîå
ïîäâåäåííîå ê ãàçó êîëè÷åñòâî òåïëîòû ïîëíîñòüþ èäåò íà
ðàáîòó, ñîâåðøåííóþ ãàçîì. Âîñïîëüçóåìñÿ ýòèì îáñòîÿòåëüñòâîì è íàéäåì êîëè÷åñòâî òåïëîòû, ïîäâåäåííîå ê ãàçó
íà ó÷àñòêàõ 1–2 è 2–3.
Îáîçíà÷èì ñîñòîÿíèå ãàçà â òî÷êå 3 ÷åðåç p3 , V3 è T3 , à
â òî÷êå 2 – ÷åðåç p2 , V2 è T2 . Ðàáîòó ãàçà À íà ó÷àñòêå
2–3 âûðàçèì ÷åðåç ïëîùàäü òðàïåöèè 23V3V2 (ðèñ.4):
A=
1
p3 + p2 V3 - V2 .
2
Èç ïîäîáèÿ òðåóãîëüíèêîâ
0 3V3 è 002V2 çàïèøåì
p3 V3
=
.
p2 V2
Ó÷èòûâàÿ, ÷òî p3V3 = RT3
è p2V2 = RT2 , èç ñîâìåñòíîÐèñ. 4
ãî ðåøåíèÿ ïðåäûäóùèõ
äâóõ óðàâíåíèé íàéäåì
2A
.
T3 - T2 =
R
Òåïåðü ìû ìîæåì çàïèñàòü ïîäâåäåííîå ê ãàçó êîëè÷åñòâî
òåïëîòû íà ó÷àñòêå 1–2:
2CA
Q12 = C T2 - T3 = R
è íà ó÷àñòêå 2–3:
2CV A
Q23 = CV T3 - T2 + A =
+ A,
R
3
ãäå CV = R — ìîëÿðíàÿ òåïëîåìêîñòü ãåëèÿ ïðè ïîñòîÿí2
íîì îáúåìå.
 ñîîòâåòñòâèè ñ ïåðâûì íà÷àëîì òåðìîäèíàìèêè,
Q12 + Q23 = A12 + A ,
ãäå A12 – èñêîìàÿ ðàáîòà ãàçà íà ó÷àñòêå 1–2. Òîãäà
îêîí÷àòåëüíî ïîëó÷èì
2 CV - C A
3
= A.
2
R
Çàäà÷à 3. Íà ðèñóíêå 5 ïîêàçàí êðóãîâîé ïðîöåññ äëÿ ν
ìîëåé ãåëèÿ, ñîñòîÿùèé èç äâóõ ó÷àñòêîâ ëèíåéíîé çàâèñèìîñòè äàâëåíèÿ ð îò îáúåìà V è îäíîé èçîáàðû. Èçâåñòíî,
÷òî íà èçîáàðå 3–1 íàä ãàçîì áûëà ñîâåðøåíà ðàáîòà À
(À > 0), à òåìïåðàòóðà ãàçà óìåíüøèëàñü â α = 4 ðàçà.
A12 = Q12 + Q23 - A =
Ñîñòîÿíèÿ 2 è 3 ïðèíàäëåæàò îäíîé èçîòåðìå. Òî÷êè 1
è 2 íà äèàãðàììå pV ëåæàò íà
ïðÿìîé, ïðîõîäÿùåé ÷åðåç íà÷àëî êîîðäèíàò. Îïðåäåëèòå:
1) òåìïåðàòóðó ãàçà â òî÷êå
1; 2) ðàáîòó ãàçà çà öèêë.
Îáîçíà÷èì òåìïåðàòóðó ãåëèÿ â òî÷êå 1 ÷åðåç T1 , òîãäà
òåìïåðàòóðà ãåëèÿ â òî÷êå 3
áóäåò T3 = αT1 . Ðàáîòà íàä
ãàçîì íà èçîáàðå ðàâíà
Ðèñ. 5
A = p1 V3 - V1 = νR T3 - T1 = νR α - 1 T1 .
Îòñþäà
T1 =
A
A
=
νR α - 1 3νR .
Ïåðåéäåì êî âòîðîìó âîïðîñó. Ðàáîòó çà öèêë Aö áóäåì
èñêàòü ÷åðåç ïëîùàäü òðåóãîëüíèêà 123:
1
Aö = p2 - p1 V3 - V1 .
2
Äëÿ èçîáàðè÷åñêîãî ïðîöåññà V : T , ïîýòîìó
V3 - V1 = V1 α - 1 .
Ïîñêîëüêó òî÷êè 1 è 2 ëåæàò íà ïðÿìîé, ïðîõîäÿùåé ÷åðåç
íà÷àëî êîîðäèíàò, òî
V
p2 = 2 p1 .
V1
Ñ äðóãîé ñòîðîíû, òî÷êè 2 è 3 ëåæàò íà èçîòåðìå, ïîýòîìó
p2V2 = p3V3 .
Ó÷èòûâàÿ, ÷òî p1 = p3 , íàõîäèì
p2 =
V3
p1 =
V1
α p1 .
Ïîñëå ïîäñòàíîâêè â âûðàæåíèå äëÿ ðàáîòû çà öèêë ïîëó÷èì
1
Aö = p1V1 α - 1 α - 1 =
2
=
1
νRT1
2
α - 1 α - 1 =
α -1 A
2
=
A
.
2
Çàäà÷à 4. Ìîëü ãåëèÿ ñîâåðøàåò ðàáîòó À â çàìêíóòîì
öèêëå (ðèñ.6), ñîñòîÿùåì èç àäèàáàòû 1–2, èçîòåðìû 2–3
è èçîáàðû 3–1. Íàéäèòå ðàáîòó, ñîâåðøåííóþ ãåëèåì â
èçîòåðìè÷åñêîì ïðîöåññå,
åñëè ðàçíîñòü òåìïåðàòóð
ìåæäó ìàêñèìàëüíîé è ìèíèìàëüíîé â öèêëå ðàâíà ∆T .
Î÷åâèäíî, ÷òî ìàêñèìàëüíàÿ òåìïåðàòóðà ãåëèÿ â öèêëå áóäåò â òî÷êå 1. Îáîçíà÷èì
ýòó òåìïåðàòóðó ÷åðåç T1 . Ìèíèìàëüíàÿ òåìïåðàòóðà ãàçà
áóäåò íà èçîòåðìå 2–3, îáîçíà÷èì åå ÷åðåç T23 . Ñîãëàñíî Ðèñ. 6
óñëîâèþ çàäà÷è,
T1 - T23 = ∆T .
Äëÿ êðóãîâîãî ïðîöåññà, â ñîîòâåòñòâèè ñ ïåðâûì íà÷àëîì
òåðìîäèíàìèêè, ñóììàðíîå ïîäâåäåííîå ê ãàçó êîëè÷åñòâî
òåïëîòû ðàâíî ðàáîòå ãàçà, ñîâåðøåííîé èì â äàííîì çàìê-
ÏÐÀÊÒÈÊÓÌ
íóòîì öèêëå:
Ðàáîòà ïàðà ðàâíà èçìåíåíèþ ïîòåíöèàëüíîé ýíåðãèè:
Q12 + Q23 + Q31 = A .
Òåïëî, ïîäâåäåííîå íà àäèàáàòå 1–2, ðàâíî íóëþ:
Q12 = 0 .
Íà èçîòåðìå 2–3 âíóòðåííÿÿ ýíåðãèÿ ãåëèÿ îñòàåòñÿ íåèçìåííîé, è ïîäâåäåííîå òåïëî ðàâíî ðàáîòå ãàçà:
Q23 = A23 .
Ïðè èçîáàðè÷åñêîì ïðîöåññå 3–1 ïîäâåäåííîå ê ãàçó òåïëî
èäåò íà óâåëè÷åíèå åãî âíóòðåííåé ýíåðãèè è íà ðàáîòó ãàçà:
Q31 = CV T1 - T23 + p31 V1 - V3 = CV + R ∆T .
Îêîí÷àòåëüíî ïîëó÷èì
A23 + CV + R ∆T = A .
Îòñþäà íàéäåì ðàáîòó ãåëèÿ íà èçîòåðìå 2–3:
5
A23 = A - CV + R ∆T = A - R∆T .
2
Çàäà÷à 5. Ïîäâèæíûé ïîðøåíü ìàññîé m, ïîäâåøåííûé íà
ïðóæèíå, äåëèò îáúåì îòêà÷àííîãî âåðòèêàëüíîãî öèëèíäðà íà äâå ÷àñòè (ðèñ.7).  ïîëîæåíèè ðàâíîâåñèÿ âûñîòà
íèæíåé ÷àñòè öèëèíäðà ðàâíà
H0 , à óäëèíåíèå ïðóæèíû ïðè
ýòîì ñîñòàâëÿåò x0 .  íèæíþþ ÷àñòü öèëèíäðà âïðûñêèâàþò ν ìîëåé âîäû. Ïîñëå òîãî
êàê âñÿ âîäà èñïàðèëàñü, ïîðøåíü ïåðåìåñòèëñÿ ââåðõ íà âåëè÷èíó x1 = αx0 ( α = 3 2 ).
Íàéäèòå: 1) óñòàíîâèâøóþñÿ
òåìïåðàòóðó ïàðà; 2) ðàáîòó,
ñîâåðøåííóþ ïàðîì. Òåïëîîòâîäîì ÷åðåç ñòåíêè öèëèíäðà ïðåÐèñ. 7
íåáðå÷ü.
Çàïèøåì óñëîâèå ìåõàíè÷åñêîãî ðàâíîâåñèÿ ïîðøíÿ äî
âïðûñêèâàíèÿ âîäû:
mg = kx0 ,
ãäå k – æåñòêîñòü ïðóæèíû. Ïîñëå èñïàðåíèÿ âîäû è
óñòàíîâëåíèÿ íîâîãî ðàâíîâåñèÿ ïîðøíÿ îáúåì ïàðà áóäåò
Vï = H0 + αx0 S ,
ãäå S – ïëîùàäü âíóòðåííåãî ïîïåðå÷íîãî ñå÷åíèÿ öèëèíäðà.
Äàâëåíèå ïàðà ïðè ýòîì áóäåò ðàâíî
pï =
mg + kx0 α - 1 αmg
=
.
S
S
Ðàññìàòðèâàÿ ïàð êàê èäåàëüíûé ãàç, èç óðàâíåíèÿ ñîñòîÿíèÿ íàéäåì òåìïåðàòóðó ïàðà:
Tï =
pïVï αmg H0 + αx0 =
.
νR
νR
Aï = W2 - W1 =
Çàäà÷à 6. Êàêóþ ìàêñèìàëüíóþ ðàáîòó ìîæíî ïîëó÷èòü
îò ïåðèîäè÷åñêè äåéñòâóþùåé òåïëîâîé ìàøèíû, íàãðåâàòåëåì êîòîðîé ñëóæèò m1 = 1 êã âîäû ïðè íà÷àëüíîé òåìïåðàòóðå T1 = 373 Ê , à õîëîäèëüíèêîì – m2 = 1 êã ëüäà ïðè
òåìïåðàòóðå T2 = 273 Ê , ê ìîìåíòó, êîãäà ðàñòàåò âåñü
ëåä? ×åìó áóäåò ðàâíà òåìïåðàòóðà âîäû íàãðåâàòåëÿ â
ýòîò ìîìåíò? Óäåëüíàÿ òåïëîòà ïëàâëåíèÿ ëüäà q =
= 80 êêàë/êã. Çàâèñèìîñòüþ òåïëîåìêîñòè âîäû îò òåìïåðàòóðû ïðåíåáðå÷ü.
Ðàáîòà, ñîâåðøàåìàÿ ëþáîé òåïëîâîé ìàøèíîé â çàìêíóòîì öèêëå, ïî ïåðâîìó íà÷àëó òåðìîäèíàìèêè ðàâíà
A = Q1 - Q2 ,
ãäå Q1 – êîëè÷åñòâî òåïëîòû, ïîäâåäåííîå ê ðàáî÷åìó òåëó
çà öèêë, à Q2 – îòâåäåííîå êîëè÷åñòâî òåïëîòû. Êîýôôèöèåíò ïîëåçíîãî äåéñòâèÿ (ÊÏÄ) òåïëîâîé ìàøèíû ðàâåí
η=
Q1 - Q2
Q
=1- 2 .
Q1
Q1
Ìàêñèìàëüíóþ ðàáîòó ìîæíî ïîëó÷èòü (òåîðåòè÷åñêè), åñëè
òåïëîâàÿ ìàøèíà áóäåò ðàáîòàòü ïî öèêëó Êàðíî. ÊÏÄ
öèêëà Êàðíî çàâèñèò òîëüêî îò òåìïåðàòóð T1 è T2 íàãðåâàòåëÿ è õîëîäèëüíèêà:
T - T2
T
ηK = 1
= 1- 2 .
T1
T1
Ñðàâíèâàÿ äâà âûðàæåíèÿ äëÿ ÊÏÄ, íàéäåì, ÷òî äëÿ öèêëà
Êàðíî
Q2 T2
=
Q1
T1 .
 íàøåì ñëó÷àå êîëè÷åñòâî òåïëîòû Q2 , îòâåäåííîå îò
ðàáî÷åãî òåëà è ïåðåäàííîå õîëîäèëüíèêó, áóäåò èäòè íà
ïëàâëåíèå ëüäà, è òåìïåðàòóðà õîëîäèëüíèêà T2 áóäåò
îñòàâàòüñÿ ïîñòîÿííîé (ïîêà íå ðàñòàåò âåñü ëåä) è ðàâíîé
273 Ê. À âîò òåìïåðàòóðà íàãðåâàòåëÿ (ãîðÿ÷àÿ âîäà) áóäåò
óìåíüøàòüñÿ ïîñëå êàæäîãî öèêëà, è ê ìîìåíòó, êîãäà ëåä
ðàñòàåò, òåìïåðàòóðà âîäû íàãðåâàòåëÿ áóäåò çàìåòíî ìåíüøå íà÷àëüíîé, ðàâíîé 373 Ê. Ñëåäîâàòåëüíî, òåìïåðàòóðà
íàãðåâàòåëÿ áóäåò ïåðåìåííîé âåëè÷èíîé.
Ïóñòü â íåêîòîðûé ïðîèçâîëüíûé ìîìåíò âðåìåíè òåìïåðàòóðà íàãðåâàòåëÿ áûëà Ò, à çà áåñêîíå÷íî ìàëîå âðåìÿ
ðàáîòû òåïëîâîé ìàøèíû îíà óìåíüøèëàñü íà dT. Êîëè÷åñòâî òåïëîòû, ïåðåäàííîå ðàáî÷åìó òåëó çà ýòî âðåìÿ, ðàâíî
dQ1 = - câm1dT ,
dQ2 = qdm2 ,
ãäå dm2 – áåñêîíå÷íî ìàëîå êîëè÷åñòâî ðàñòàÿâøåãî ëüäà.
Âîñïîëüçîâàâøèñü ñîîòíîøåíèåì ìåæäó Q è Ò äëÿ öèêëà
Êàðíî, ïîëó÷èì
-
kx2 mgx0
W1 = 0 =
.
2
2
Ïîòåíöèàëüíàÿ ýíåðãèÿ â êîíå÷íîì ñîñòîÿíèè ñîñòàâëÿåò
α2mgx0 9
= mgx0 .
2
8
ãäå c⠖ óäåëüíàÿ òåïëîåìêîñòü âîäû. Êîëè÷åñòâî òåïëîòû,
ïåðåäàííîå õîëîäèëüíèêó, ñîñòàâëÿåò
Ðàáîòà, ñîâåðøåííàÿ ïàðîì, ïîéäåò íà ïðèðàùåíèå ïîòåíöèàëüíîé ýíåðãèè ïîðøíÿ è ïðóæèíû. Åñëè îòñ÷èòûâàòü
ïîòåíöèàëüíóþ ýíåðãèþ ïîðøíÿ îò åãî ïîëîæåíèÿ ïðè
îòñóòñòâèè âîäû â öèëèíäðå, òî ñóììàðíàÿ ïîòåíöèàëüíàÿ
ýíåðãèÿ ïîðøíÿ è ïðóæèíû â íà÷àëüíûé ìîìåíò ðàâíà
W2 =
"#
ÀÁÈÒÓÐÈÅÍÒÀ
2
mgx0 α2 + 1
kx02 α - 1
.
+ mgαx0 =
2
2
qdm2
T
= 2 .
câm1dT
T
Ïîñëå ðàçäåëåíèÿ ïåðåìåííûõ Ò è m2 ýòî óðàâíåíèå áóäåò
èìåòü âèä
dT
qdm2
=.
T
câm1T2
"$
ÊÂÀÍT 2007/¹3
Ïðîèíòåãðèðóåì îáå ÷àñòè äàííîãî óðàâíåíèÿ:
Tê
ò
T1
dT
q
=T
câm1T2
m2
ò dm2 ,
0
ãäå Tê – êîíå÷íàÿ òåìïåðàòóðà âîäû â íàãðåâàòåëå ê ìîìåíòó, êîãäà âåñü ëåä ðàñòàåò. Ïîñëå èíòåãðèðîâàíèÿ ïîëó÷èì
T
qm2
,
ln ê = T1
câm1T2
îòêóäà íàéäåì
æ qm2 ö
Tê = T1 exp ç = 278, 3 Ê .
è câm1T2 ÷ø
Òåïåðü ìû ìîæåì îïðåäåëèòü ñóììàðíîå êîëè÷åñòâî òåïëîòû, ïîëó÷åííîå îò íàãðåâàòåëÿ ê ìîìåíòó ïîëíîãî òàÿíèÿ
ëüäà:
Q1 = câm1 T1 - Tê .
Ñóììàðíîå êîëè÷åñòâî òåïëîòû, ïåðåäàííîå ïðè ýòîì õîëîäèëüíèêó, ðàâíî
Q2 = qm2 .
Ñëåäîâàòåëüíî, îò òåïëîâîé ìàøèíû ìîæíî ïîëó÷èòü ìàêñèìàëüíóþ ðàáîòó
Amax = Q1 - Q2 = câm1 T1 - Tê - qm2 = 61,5 êÄæ .
Óïðàæíåíèÿ
1. Ìîëü ãåëèÿ, ðàñøèðÿÿñü â ïðîöåññå 1–2 (ðèñ.8), ãäå åãî
äàâëåíèå ð ìåíÿåòñÿ ïðÿìî ïðîïîðöèîíàëüíî åãî îáúåìó V,
ñîâåðøàåò ðàáîòó À. Èç ñîñòîÿíèÿ 2 ãåëèé ðàñøèðÿåòñÿ â
ïðîöåññå 2–3, â êîòîðîì åãî òåïëîåìêîñòü îñòàåòñÿ ïîñòîÿííîé
è ðàâíîé Ñ = R/2. Êàêóþ ðàáîòó ñîâåðøèò ãåëèé â ïðîöåññå
Ôîðìóëû
ãåîìåòðèè
ïîìîãàþò
àëãåáðå
Â.ÌÈÐÎØÈÍ
Â
ØÊÎËÜÍÎÌ ÊÓÐÑÅ ÌÀÒÅÌÀÒÈÊÈ ÏÐÈÂÎÄßÒÑß ÒÐÈ
ôîðìóëû, ïîçâîëÿþùèå íàõîäèòü:
à) ðàññòîÿíèå ìåæäó òî÷êàìè ñ êîîðäèíàòàìè x1 è x2 íà
÷èñëîâîé ïðÿìîé: ýòî ìîäóëü èõ ðàçíîñòè, ò.å. d = x2 - x1 ;
á) ðàññòîÿíèå ìåæäó òî÷êàìè x1; y1 è x2; y2 ÷èñëîâîé
x2 - x12 + y2 - y12 ;
ðàññòîÿíèå îò òî÷êè x0; y0 äî
ïëîñêîñòè: d =
â)
óðàâíåíèåì ax + by + c = 0 : d =
ïðÿìîé, çàäàííîé
ax0 + by0 + c
a2 + b2
.
Ðèñ. 8
Ðèñ. 9
2–3, åñëè òåìïåðàòóðû íà÷àëüíîãî (1) è êîíå÷íîãî (3) ñîñòîÿíèé ðàâíû?
2. Öèêë äëÿ ν ìîëåé ãåëèÿ ñîñòîèò èç äâóõ ó÷àñòêîâ ëèíåéíîé
çàâèñèìîñòè äàâëåíèÿ ð îò îáúåìà V è îäíîé èçîõîðû (ðèñ.9).
 èçîõîðè÷åñêîì ïðîöåññå 1–2 îò ãàçà áûëî îòâåäåíî êîëè÷åñòâî
òåïëîòû Q (Q > 0), è åãî òåìïåðàòóðà óìåíüøèëàñü â 4 ðàçà.
Òåìïåðàòóðû â ñîñòîÿíèÿõ 2 è 3 ðàâíû. Òî÷êè 1 è 3 íà äèàãðàììå
pV ëåæàò íà ïðÿìîé, ïðîõîäÿùåé ÷åðåç íà÷àëî êîîðäèíàò. 1)
Íàéäèòå òåìïåðàòóðó T1 â òî÷êå 1. 2) Íàéäèòå ðàáîòó ãàçà çà
öèêë.
3. Ìîëü ãåëèÿ ñîâåðøàåò ðàáîòó À â çàìêíóòîì öèêëå, ñîñòîÿùåì èç èçîáàðû 1–2, èçîõîðû 2–3 è àäèàáàòè÷åñêîãî ïðîöåññà 3–1 (ðèñ.10). Ñêîëüêî
òåïëà áûëî ïîäâåäåíî ê ãàçó â
Ðèñ. 10
èçîáàðè÷åñêîì ïðîöåññå, åñëè
ðàçíîñòü ìàêñèìàëüíîé è ìèíèìàëüíîé òåìïåðàòóð ãåëèÿ â
öèêëå ðàâíà ∆T ?
Äîâîëüíî ÷àñòî óäàåòñÿ èñïîëüçîâàòü ýòè ôîðìóëû ïðè
ðåøåíèè àëãåáðàè÷åñêèõ çàäà÷. Äëÿ ýòîãî, êàê ïðàâèëî,
íóæíî èñòîëêîâàòü äàííîå àëãåáðàè÷åñêîå âûðàæåíèå êàê
ðàññòîÿíèå èëè ñóììó ðàññòîÿíèé äî íåêîòîðûõ òî÷åê èëè
ïðÿìûõ. Ñ òàêèìè çàäà÷àìè ìû è ñîáèðàåìñÿ âàñ ïîçíàêîìèòü.
Ñóììà ðàññòîÿíèé
Çàäà÷à 1. Íàéäèòå ìèíèìóì âûðàæåíèÿ
f x, y =
x - 32 + y - 42
+ x 2 + y2 .
Ðåøåíèå. Äàííîå âûðàæåíèå ïðåäñòàâëÿåò ñóììó ðàññòîÿíèé îò íåêîòîðîé òî÷êè M(x; y) êîîðäèíàòíîé ïëîñêîñòè äî
äâóõ òî÷åê: K 3;4 è íà÷àëà êîîðäèíàò O 0;0 .
Èñïîëüçóÿ èçâåñòíîå «íåðàâåíñòâî òðåóãîëüíèêà», ïîëó÷èì, ÷òî ñóììà ðàññòîÿíèé MK + MO íå ìîæåò áûòü ìåíüøå
ðàññòîÿíèÿ KO, ïðè÷åì ìèíèìóì äîñòèãàåòñÿ äëÿ ëþáîé
òî÷êè M, ëåæàùåé íà îòðåçêå KO. Èòàê, MK + MO ≥ OK =
= 5.
Îòâåò: 5.
Çàìå÷àíèå. Äëÿ òî÷åê, ëåæàùèõ íà êîîðäèíàòíîé îñè,
íåðàâåíñòâî ìîæåò áûòü çàïèñàíî â âèäå x - a + x - b =
= a - b Û x - a x - b £ 0 .
Çàäà÷à 2 (ÌÃÓ, ìåõìàò). Íàéäèòå ìèíèìóì âûðàæåíèÿ
f x, y =
x - 2 2 + y - 3 2
+ x-y .