Нахождение области определения функции. 1) F(x)=ctgx*tgx = 1
реклама

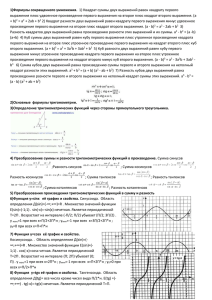
Нахождение области определения функции. 1) F(x)=ctgx*tgx = 1 cosx≠0 и sinx≠0 x≠π/2 + πk, k x≠πk, k Ответ : x≠πk/2, k 2) D (f) y(x)= - y(x)= -- = -- -5 ≤ 2x-5 ≤ 5 и x=0 0 ≤ 2x ≤ 10 x 0≤x≤5 Ответ 3) Сколько целых чисел из отрезка y= ,х Є D(f) - ? + x, Sin2πx = 0 2πx=πk, X= , k Ответ : 32 числа 4) Найти сумму целых чисел, входящих в D(f) функции f(x)= Ответ : (2; 9] Сумма целых чисел равна 28 Нахождение E(f) 1. (2, (1) + 1, (8)) 4 Ответ : 2. F(x) = , знаменатель дроби достигает min при x=-2 Дробь и второе слагаемое при данном значении х достигают максимума. Cosx=1 X=2 n Ответ: Наиб: +1 3. Найти наиб. и наим. значение функции F(x)=-sin2x+cosx+ =-(1-cos2x)+cosx+ cos2x+cosx Наиб. при cosx=1 Наим. при cosx= Второй способ: применение производной. Ответ : 4. решим уравнение относительно переменной t с параметром y. 1) 2) 3) Ответ: 2-ой способ: Обозначим 3x+1 = t ≤ Ответ : «Графики» 1) -- sin2x = Y=1 Исключить cosx-sinx=0 cosx=sinx x= Ответ: прямая y=1, x 2) y = x 2 1) y = = x 2 2) y = = x- = = = = -2 , x 0 x 1 Ответ : y= - 2, при x 2; y= , при x 2 , x 3) f(f(f(x))), если f(x)= f(f(x))= = f(f(f(x))) = = = = =x Ответ : y=x, x 0, x 1 4) y= y=1, cosx y=-1, cosx 0 «Лабиринт» 1) f(x) = 2x-3 f(q(x)) = q(x) - ? f(x-1) = 2(x-1) – 1 f(x) = 2x – 1, тогда 2q(x)-1 = 2q(x) = f(q(x)) = 2q(x) – 1 Ответ: q(x) = +1 2) f(sinx) + f(cosx) = 3 f(sinx) + f(cosx) =1+2= f(x) - ? Ответ: f(x) = 3) 3f(x) = 3f(x)= Ответ : f(x) = 4) f(sin2x) = f(sin2x) = Ответ : f(x)=x = «Коктейль» 1. Найти функцию обратную данной , x (- 2. Замена 3. Чет и нечет. нечет - нечет