sinx=-1/2
реклама

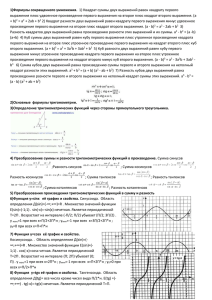
«Отбор корней при решении тригонометрических уравнений, используя свойство периодичности тригонометрических функций» С1 Учитель Степушкина Н.Ю. 1. Вычислить: sin 420°; cos 390°; tg 585°; ctg 390°; sin 750°; cos 720°; sin 780;cos 405°; tg 240°; ctg 750°; sin(-1080°); cos(-1110); tg(-225°); ctg(-210°) 2. Каким свойством тригонометрических функций воспользовались? 3. Указать Т(sin) ; Т(сos) ; Т(tg); Т(сtg). 4. C помощью тригонометра решить уравнения: sinx=1/2; сosx=1/2; tgx=1/2;ctgx=1/2; sinx=-1/2; cosx=-1/2; tgx=-1; ctgx=1; cosx=1; sinx=1;sinx=5;cosx=-3. 5. C помощью тригонометра отобрать корни тригонометрических уравнений на отрезках [0;п/2] ; [п/2; п]; [0;-п] ; [3п/2;2п] ; [0;п] : sinx=-√3/2; sinx= √3/2; cosx= √2/2; cosx=- √2/2; tgx=1; ctgx=-1. Вычислить : 1. sin1470°; Ответ : а) √ 3/2; б) √ 2/2; в) 1; м) 1/2. 2. cos1125°; Ответ : а) 1;б) √ 3/2; в) 1/2; о) √ 2/2. 3. tgx 240°; Ответ : а) 1;б) √3/3;в) 2; л) √ 3. Найти корни уравнений, принадлежащие отрезку [п/2;3п/2]: 4. sinx=1/2; Ответ: а) п/6;б) нет корней; в) 4п/3; о) 5п/6. 5. cosx=1/2; Ответ : а) п/3;б) п/6;в) 4п/3 д) нет корней. 6. tgx=1/2; Ответ : а) нет корней; б) arctg1/2; в) 5п/6; е) arctg1/2+п. 7. Найдите корни уравнения сosx=3/4, принадлежащие отрезку [7п/2;9п/2]. Ответ : а) arccos3/4; б) arccos3/4;- arccos3/4;в) п/6;- п/6;ц) arccos3/4 + 4п; -arccos3/4 + 4п. • Ответ : 1 2 3 4 5 6 7 М О Л О Д Е Ц • Решить уравнение 2sin2х + cosх + 4sinх + 1 = 0. Указать корни, принадлежащие отрезку [5п/2;7п/2]. Решение: 1. 4sinxcosx + cosx + 4 sinx + 1 = 0; cosx(4sinx + 1) + (4sinx + 1) = 0; 4sinx + 1 =0 или cosx + 1 = 0; sinx = -1/4 или соsx = -1; x = -arcsin1/4 + 2пn, или x = п + 2пn x = п + arcsin1/4 + 2пn , n c N 2. Отбор корней на отрезке [5п/2;7п/2]: а) x = п + 2пn, n c N б) x = -arcsin1/4 + 2пn Решается традиционными способами : x = 3п x = п + аrcsin1/4 + 2пn, n c N ? • Попробовать решить самостоятельно: 1. sinx = -1/3 на отрезке [-3п/2;-п] Ответ: нет корней. 2. сosx = 1 на отрезке [5п/2;7п/2] Ответ : нет корней. 3. tgx = -1 на отрезке [3п/2;5п/2] Ответ : 7п/4. Домашнее задание (задания уровня С1) : 1. Решить уравнение 2sin^2x – cosx – 1 = 0. Указать корни принадлежащие отрезку [3п;4п]. 2. Решить уравнение 7sin^2x + 4sinxcosx – 3 cos^2x = 0. Указать корни, принадлежащие отрезку [3п/2;5п/2]. 3. Самому составить простейшие тригонометрические уравнения, задать отрезок и выбрать корни на данном отрезке.