Геометрия 10-12 класс - ФКОУ В(С)ОШ ГУФСИН России по
реклама

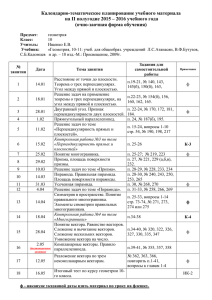
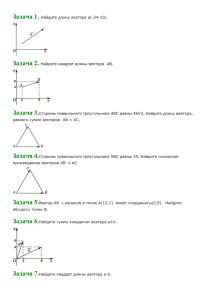
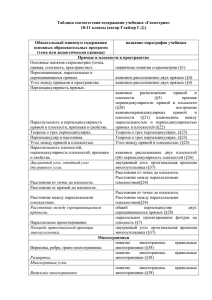
Пояснительная записка Данная рабочая программа составлена в соответствии с требованиями Федерального Государственного образовательного стандарта, программы по геометрии 10-11 классы, составитель Т.А.Бурмистрова, 2011г. и учебного плана ФКОУ В(С)ОШ ГУФСИН России по Иркутской области. Геометрия – один из важнейших компонентов математического образования, необходимый для приобретения конкретных знаний о пространстве и практически значимых умений, формирования языка описания объектов окружающего мира, для развития пространственного воображения и интуиции, математической культуры, для эстетического воспитания учащихся. Изучение геометрии вносит вклад в развитие логического мышления, в формирование понятия доказательства. Программа рассчитана на обучение учащихся 10-12 общеобразовательных классов. Данная программа конкретизирует содержание стандарта, дает распределение учебных часов по разделам курса, последовательность изучения тем и разделов с учетом межпредметных и внутрипредметных связей, логики учебного процесса, возрастных особенностей учащихся. Цель изучения курса геометрии в 10-11 классах — систематическое изучение свойств геометрических тел в пространстве, развитие пространственных представлений учащихся, освоение способов вычисления практически важных геометрических величин и дальнейшее развитие логического мышления учащихся. Курсу присущи систематизирующий и обобщающий характер изложения, направленность на закрепление и развитие умений и навыков, полученных в неполной средней школе. При доказательстве теорем и решении задач активно используются изученные в курсе планиметрии свойства геометрических фигур, применяются геометрические преобразования, векторы и координаты. Высокий уровень абстрактности изучаемого материала, логическая строгость систематического изложения соединяются с привлечением наглядности на всех этапах учебного процесса и постоянным обращением к опыту учащихся. Умения изображать важнейшие геометрические тела, вычислять их объемы и площади поверхностей имеют большую практическую значимость. В соответствии с учебным планом ФБОУ В(С)ОШ ГУФСИН России по Иркутской области на изучение геометрии в 10 классе отводится 1 час в неделю, 35 часов в год, в 11 классе отводится 1 час в неделю, 35 часов в год соответственно и в 12 классе 1 час в неделю и 34 часа год. Итого курс рассчитан на 104 часа. Преподавание ведётся по учебнику «Геометрия 10-11» автор Атанасян Л.С. и др, (изд. Просвещение, М. 2011). Реализация данной программы способствует использованию разнообразных форм организации учебного процесса, внедрению современных методов обучения и педагогических технологий. В ходе ее достижения решаются задачи: изучение свойств пространственных тел, формирование умения применять полученные знания для решения практических задач. В результате прохождения программного материала обучающийся имеет представление о: 1).математике как универсальном языке науки, средстве моделирования явлений и процессов, об идеях и методах математики; 2).значении практики и вопросов, возникающих в самой математике для формирования и развития математической науки; 3).универсальном характере законов логики математических рассуждений, их применимости во всех областях человеческой деятельности; знает (предметно-информационная составляющая результата образования): каким образом геометрия возникла из практических задач землемерия; примеры геометрических объектов и утверждений о них, важных для практики; умеет (деятельностно-коммуникативная составляющая результата образования): овладевать математическими знаниями и умениями, необходимыми в повседневной жизни, для изучения школьных естественнонаучных дисциплин на базовом уровне, для получения образования в областях, не требующих углубленной математической подготовки; Математическое образование является обязательной и неотъемлемой частью общего образования на всех ступенях школы. Обучение математике в основной школе направлено на достижение следующих целей: 1) в направлении личностного развития: Формирование представлений о математике как части общечеловеческой культуры, о значимости математики в развитии цивилизации и современного общества; Развитие логического и критического мышления, культуры речи, способности к умственному эксперименту; Формирование интеллектуальной честности и объективности, способности к преодолению мыслительных стереотипов, вытекающих из обыденного опыта; Воспитание качеств личности, обеспечивающих социальную мобильность, способность принимать самостоятельные решения; Формирование качеств мышления, необходимых для адаптации в современном информационном обществе; Развитие интереса к математическому творчеству и математических способностей; 2) в метапредметном направлении: Развитие представлений о математике как форме описания и методе познания действительности, создание условий для приобретения первоначального опыта математического моделирования; Формирование общих способов интеллектуальной деятельности, характерных для математики и являющихся основой познавательной культуры, значимой для различных сфер человеческой деятельности; 3) в предметном направлении: Овладение математическими знаниями и умениями, необходимыми для продолжения образования, изучения смежных дисциплин, применения в повседневной жизни; Создание фундамента для математического развития, формирования механизмов мышления, характерных для математической деятельности. Общие учебные умения, навыки и способы деятельности Овладение общими умениями, навыками и способами деятельности как существенными элементами культуры является необходимым условием развития и социализации школьников. Познавательная деятельность. Использование для познания окружающего мира различных методов (наблюдение, измерение, опыт, эксперимент, моделирование и др.). Определение структуры объекта познания, поиск и выделение значимых функциональных связей и отношений между частями целого. Умение разделять процессы на этапы, звенья. Выделение характерных причинно – следственных связей. Определение адекватных способов решения учебной задачи на основе заданных алгоритмов. Комбинирование известных алгоритмов деятельности в ситуациях, не предполагающих стандартное применение одного из них. Сравнение, сопоставление, классификация, ранжирование объектов по одному или нескольким предложенным основаниям, критериям. Умение различать факт, мнение, доказательство, гипотезу, аксиому. Исследование несложных практических ситуаций, выдвижение предложений, понимание необходимости их проверки на практике. Творческое решение учебных и практических задач: умение мотивированно отказываться от образца, искать оригинальные решения; самостоятельное выполнение различных творческих работ; участие в проектной деятельности. Регулятивные УУД. Самостоятельная организация учебной деятельности (постановка цели, планирование, определение оптимального соотношения цели и средств и др.). Владение навыками контроля и оценки своей деятельности, умением предвидеть результаты своих действий. Поиск и устранение причин возникших трудностей. Оценивание своих учебных достижений, поведения, черт своей личности, своего физического и эмоционального состояния. Осознанное определение сферы своих интересов и возможностей. Соблюдение норм поведения в окружающей среде, правил здорового образа жизни. Личностными результаты: согласование и координация деятельности с другими ее участниками; объективное оценивание своего вклада в решение общих задач коллектива; учет особенностей различного ролевого поведения (лидер, подчиненный и др.). Оценивание своей деятельности с точки зрения нравственных, правовых норм, эстетических ценностей. Использование своих прав и выполнение своих обязанностей как гражданина, члена общества и учебного коллектива. Познавательные УУД: – анализировать, сравнивать, классифицировать и обобщать факты и явления; – осуществлять сравнение, сериацию и классификацию, самостоятельно выбирая основания и критерии для указанных логических операций; строить классификацию путём дихотомического деления (на основе отрицания); – строить логически обоснованное рассуждение, включающее установление причинноследственных связей; – создавать математические модели; – составлять тезисы, различные виды планов (простых, сложных и т.п.). Преобразовывать информацию из одного вида в другой (таблицу в текст, диаграмму и пр.); – вычитывать все уровни текстовой информации. – уметь определять возможные источники необходимых сведений, производить поиск информации, анализировать и оценивать её достоверность. – понимая позицию другого человека, различать в его речи: мнение (точку зрения), доказательство (аргументы), факты; гипотезы, аксиомы, теории. Для этого самостоятельно использовать различные виды чтения (изучающее, просмотровое, ознакомительное, поисковое), приёмы слушания. – самому создавать источники информации разного типа и для разных аудиторий, соблюдать информационную гигиену и правила информационной безопасности; – уметь использовать компьютерные и коммуникационные технологии как инструмент для достижения своих целей. Уметь выбирать адекватные задаче инструментальные программноаппаратные средства и сервисы. Средством формирования познавательных УУД служат учебный материал и прежде всего продуктивные задания учебника. – Использование математических знаний для решения различных математических задач и оценки полученных результатов. – Совокупность умений по использованию доказательной математической речи. – Совокупность умений по работе с информацией, в том числе и с различными математическими текстами. – Умения использовать математические средства для изучения и описания реальных процессов и явлений. – Независимость и критичность мышления. – Воля и настойчивость в достижении цели. Коммуникативные УУД: – самостоятельно организовывать учебное взаимодействие в группе (определять общие цели, договариваться друг с другом и т.д.); – отстаивая свою точку зрения, приводить аргументы, подтверждая их фактами; – в дискуссии уметь выдвинуть контраргументы; – учиться критично относиться к своему мнению, с достоинством признавать ошибочность своего мнения (если оно таково) и корректировать его; – понимая позицию другого, различать в его речи: мнение (точку зрения), доказательство (аргументы), факты; гипотезы, аксиомы, теории; – уметь взглянуть на ситуацию с иной позиции и договариваться с людьми иных позиций. Средством формирования коммуникативных УУД служат технология проблемного обучения, организация работы в малых группах, также использование на уроках технологии личностноориентированного и системно- деятельностного обучения. Информационно – коммуникативная деятельность. Адекватное восприятие устной речи и способность передавать содержание прослушанного текста в сжатом или развернутом виде в соответствии с целью учебного задания. Осознанное беглое чтение текстов различных стилей и жанров, проведение информационно – смыслового анализа текста. Использование различных видов чтения Владение монологической и диалогической речью. Умение вступать в речевое общение, участвовать в диалоге. Создание письменных высказываний, адекватно передающих прослушанную и прочитанную информацию с заданной степенью свернутости (кратко, выборочно, полно). Составление плана, тезисов, конспекта. Приведение примеров, подбор аргументов, формулирование выводов. Отражение в письменной или устной форме результатов своей деятельности. Умение перефразировать мысль. Выбор и использование выразительных средств языка и знаковых систем (текст, таблица, схема, аудиовизуальный ряд и др.) в соответствии с коммуникативной задачей, сферой и ситуацией общения. Использование для решения познавательных и коммуникативных задач различных источников информации, включая энциклопедии, словари, справочники, Интернет – ресурсы и другие базы данных. Использование информационных технологий позволяет расширить рамки изучения предмета. Особое место отводиться для самостоятельной деятельности ученика во время урока и при выполнении домашних заданий по математике. Формы контроля: Контрольные работы, самостоятельные работы, математический диктант, тестирование Учебно- тематическое планирование 10 класс № Название разделов и тем п/п 1 Повторение курса геометрии 9 класса 2 Введение(аксиомы стереометрии и их следствия) 3 Параллельность прямых и плоскостей Перпендикулярность прямых и плоскостей 4 Многогранники 5 Повторение итого Количество Количество часов часов 7 2 3 7 16 8 17 8 12 3 3 35 Содержание учебного материала Введение. Аксиомы стереометрии. Следствия из аксиом. Знать: Основные понятия и аксиомы стереометрии (точка, прямая, плоскость, пространство); Уметь: изображать прямые и плоскости в пространстве; применять аксиомы при решении задач Глава 1. Параллельность прямых и плоскостей. Знать: Пересекающиеся, параллельные и скрещивающиеся прямые. Угол между прямыми в пространстве; параллельное проектирование; изображение пространственных фигур Уметь: Изображать различными способами пространственные фигуры на плоскости, строить сечения и применять знания при решении задач. Прямые и плоскости в пространстве. Основные понятия стереометрии (точка, прямая, плоскость, пространство). Пересекающиеся, параллельные и скрещивающиеся прямые. Угол между прямыми в пространстве. Перпендикулярность прямых. Параллельность и перпендикулярность прямой и плоскости, признаки и свойства. Теорема о трех перпендикулярах. Перпендикуляр и наклонная. Угол между прямой и плоскостью. Глава 2. Перпендикулярность прямых и плоскостей. Знать: Перпендикулярность прямых. Параллельность и перпендикулярность прямой и плоскости, признаки и свойства. Теорема о трех перпендикулярах. Перпендикуляр и наклонная. Угол между прямой и плоскостью. ; расстояния от точки до плоскости; расстояние от прямой до плоскости; расстояние между параллельными плоскостями; расстояние между скрещивающимися прямыми; Уметь: применять знания к решению задач. Параллельность плоскостей, перпендикулярность плоскостей, признаки и свойства. Двугранный угол, линейный угол двугранного угла. Расстояния от точки до плоскости. Расстояние от прямой до плоскости. Расстояние между параллельными плоскостями. Расстояние между скрещивающимися прямыми. Параллельное проектирование. Площадь ортогональной проекции многоугольника. Изображение пространственных фигур. Глава 3. Многогранники. Понятие многогранника. Призма. Пирамида. Правильные многогранники. Основная цель – познакомить учащихся с основными видами многогранников (призма, пирамида, усеченная пирамида), с формулой Эйлера для выпуклых многогранников, с правильными многогранниками и элементами их симметрии. Учебно-тематический план 11 класс № п/п Название разделов и тем Количес Количество часов тво часов 3 1 Повторение 2 Многогранники 10 3 Векторы в пространстве 14 4 Метод координат в пространстве. Движения 6 5 Повторение 2 Итого: 35 ч. Содержание учебного материала Раздел 1. Многогранники. Тема 1.1. Понятия многогранника. Призма Требования к знаниям: понятия многогранника, определения призмы и ее элементов, виды призм в зависимости от ребер, понятие площади поверхности призм, формулу для нахождения площади поверхности призм, прямая и наклонная призма, формула для вычисления боковой поверхности наклонной призмы. Требования к умениям: применять изученный теоретический материал при решении задач на вычисления и построения, изображать развертки различных видов призм ( тетраэдра, куба , параллелепипеда) находить их полные и боковые поверхности, применять формулу для вычисления боковой поверхности наклонных призм при решении задач на вычисления. Содержания учебного материала Понятия многогранника. Выпуклые и невыпуклые многогранники; виды многогранников (тетраэдр, октаэдр, параллелепипед). Призма (прямая, наклонная). Площадь полной и боковой поверхности призмы. Изображение призмы и построение ее сечений. практическое занятие Решение задач на нахождение полной и боковой поверхности призмы. Изображение призмы и построение ее сечений. Тема 1.2. Пирамида Требования к знаниям: понятия пирамиды, виды пирамид (правильная пирамида, наклонная пирамида, усеченная пирамида), формулу для вычисления площади полной и боковой поверхности, понятия сечения пирамиды плоскостью, свойства пирамид. Требования к умениям: решать задачи используя изученную теорию; находить площади поверхностей всех видов пирамид используя развертки данных фигур, применять свойства пирамид при решении задач Содержания учебного материала Пирамида. Построение пирамиды и ее плоских сечений. Усеченная пирамида. Правильная пирамида. практическое занятие Решение задач на нахождение полной и боковой поверхности пирамиды. Использование свойств пирамиды при решении задач. Тема 1.3. Правильные многогранники Требования к знаниям: определения правильных многогранников (тетраэдра октаэдра, икосаэдра, куба),сколько центров симметрии имеет каждая фигура. Требования к умениям: выполнять рисунки к задачам, составлять план решения задачи, делать краткую запись, строить фигуры симметричные относительно центра и относительно прямой, рисовать развертки всех правильных многогранников. Содержание учебного материала Симметрия в пространстве: точки симметричные относительно центра, точки симметричные относительно прямой. Построение симметричных фигур. Понятия правильного многогранника. Развертки поверхностей всех видов правильных многогранников. Оси симметрии правильных многогранников. практическое занятие Построение симметричных фигур. Раздел 2. Векторы в пространстве Тема 2.1. Понятие вектора в пространстве Требования к знаниям: понятие вектора в пространстве, ненулевого вектора, коллинеарных векторов, сонаправленных векторов, длины вектора, определение равных векторов. Требования к умениям: строить векторы на чертежах, находить их длины. Содержание учебного материала Понятие вектора. Равенство векторов. практическое занятие Решение задач на нахождение длины векторов, построение векторов. Тема 2.2. Сложение и вычитание векторов. Умножение вектора на число. Требования к знаниям: правила сложения двух и нескольких векторов, законы сложения, правило и законы умножения вектора на число. Требования к умениям: применять правила треугольника и многоугольника для нахождения суммы векторов, выполнять умножение вектора на положительное число, умножение вектора на отрицательное число. Содержание учебного материала. Понятия суммы двух векторов. Сложение и вычитание векторов. Сумма нескольких векторов. Умножение вектора на число. практическое занятие Решение задач на нахождение суммы векторов и применение законов умножения вектор анна число. Тема 2.3. Компланарные векторы Требования к знаниям: определения компланарных векторов, теорему о разложении вектора по трем некомпланарным векторам, правила параллелограмма Требования к умениям: используя теорему о разложении вектора по трем некомпланарным векторам, решать задачи, применять правила параллелепипеда для нахождения суммы векторов. Содержания учебного материала. Определение компланарных векторов. Правило параллелепипеда. Разложение вектора по трем некомпланарным векторам. практическое занятие Решение задач по теме: «Компланарные вектора». Раздел 3. Метод координат в пространстве. Движения Тема 3.1. Координаты точки и координаты вектора. Требования к знаниям: определение прямоугольной системе координат в пространстве, правила для нахождения суммы, разности двух векторов, формулы для нахождения середины отрезка, длины отрезка, расстояния между двумя точками. Требования к умениям: находить координаты вектора, по изученным формулам находить середину отрезка, длину вектора, расстояния между двумя точками. Содержания учебного материала. Прямоугольная система координат в пространстве. Координаты вектора. Связь между координатами векторов и координатами точек. Простейшие задачи в координатах (координаты середины отрезка, вычисление длины вектора по его координатам, расстояние между двумя точками). практическое занятие Решение простейших задач в координатах. Тема 3.2.Скалярное произведение векторов Требования к знаниям: определения скалярного произведение векторов, формулу для вычисления скалярного произведения векторов, свойства скалярного произведения, формулу для вычисления углов между прямыми и плоскостями, уравнения плоскости. Требования к умениям: по изученным формулам решать задачи. Содержания учебного материала. Скалярное произведение векторов. Угол между векторами. Свойства скалярного произведения. Вычисление углов между прямыми и плоскостями. Уравнение плоскости. практическое занятие Применение изученных формул при решении задач. Тема 3.3. Движения Требования к знаниям: определения параллельного переноса, осевой и центральной симметрии. Требования к умениям: строить фигуры симметричные относительно центра, относительно оси, уметь производить параллельный перенос данной фигуры на данное расстояние (вектор), доказывать, что данные преобразования являются движением. Содержание учебного материала. Центральная симметрия. Осевая симметрия. Зеркальная симметрия. Параллельный перенос. практическое занятие Построение фигур симметричных относительно центра, оси. Осуществлять параллельный перенос фигур на данное расстояние. Учебно-тематический план 12 класс № Тема Количество часов 1 Повторение 4 Количество часов по программе 2 2 3 4 Цилиндр, конус, шар Объемы тел Повторение итого 10 16 4 34 13 15 6 Содержание учебного материала Цилиндр, конус, шар Основные элементы сферы и шара. Взаимное расположение сферы и плоскости. Многогранники, вписанные в сферу. Многогранники, описанные около сферы. Цилиндр и конус. Фигуры вращения. Цель: дать учащимся систематические сведения об основных видах тел вращения. Изучение круглых тел (цилиндра, конуса, шара) завершает изучение системы основных пространственных геометрических тел. В ходе знакомства с теоретическим материалом темы значительно развиваются пространственные представления учащихся: круглые тела рассматривать на примере конкретных геометрических тел, изучать взаимное расположение круглых тел и плоскостей (касательные и секущие плоскости), ознакомить с понятиями описанных и вписанных призм и пирамид. Решение большого количества задач позволяет продолжить работу по формированию логических и графических умений. В данной теме обобщаются сведения из планиметрии об окружности и круге, о взаимном расположении прямой и окружности, о вписанных и описанных окружностях. Здесь учащиеся знакомятся с основными фигурами вращения, выясняют их свойства, учатся их изображать и решать задачи на фигуры вращения. Формированию более глубоких представлений учащихся могут служить задачи на комбинации многогранников и фигур вращения. Объем и площадь поверхности Понятие объема и его свойства. Объем цилиндра, прямоугольного параллелепипеда и призмы. Принцип Кавальери. Объем пирамиды. Объем конуса и усеченного конуса. Объем шара и его частей. Площадь поверхности многогранника, цилиндра, конуса, усеченного конуса. Площадь поверхности шара и его частей. Цель: продолжить систематическое изучение многогранников и тел вращения в ходе решения задач на вычисление их объемов. Понятие объема вводить по аналогии с понятием площади плоской фигуры и формулировать основные свойства объемов. Существование и единственность объема тела в школьном курсе математики приходится принимать без доказательства, так как вопрос об объемах принадлежит, по существу, к трудным разделам высшей математики. Поэтому нужные результаты устанавливать, руководствуясь больше наглядными соображениями. Учебный материал главы в основном должен усвоиться в процессе решения задач. Изучение объемов обобщает и систематизирует материал планиметрии о площадях плоских фигур. При выводе формул объемов используется принцип Кавальери. Это позволяет чисто геометрическими методами, без использования интеграла или предельного перехода, найти объемы основных пространственных фигур, включая объем шара и его частей. Практическая направленность этой темы определяется большим количеством разнообразных задач на вычисление объемов и площадей поверхностей. Повторение Цель: повторить и обобщить знания и умения, учащихся через решение задач по следующим темам: метод координат в пространстве; многогранники; тела вращения; объёмы многогранников и тел вращения Знать: вершины, ребра, грани многогранника, понятия развертки, многогранных углов. Выпуклые многогранники. Теорема Эйлера. Призма, ее основания, боковые ребра, высота, боковая поверхность. Прямая и наклонная призма. Правильная призма. Параллелепипед. Куб. Пирамида, ее основание, боковые ребра, высота, боковая поверхность. Треугольная пирамида. Правильная пирамида. Усеченная пирамида. Симметрии в кубе, в параллелепипеде. Понятие о симметрии в пространстве (центральная, осевая, зеркальная). Примеры симметрий в окружающем мире. Сечения куба, призмы, пирамиды. Представление о правильных многогранниках (тетраэдр, куб, октаэдр, додекаэдр и икосаэдр). Уметь: применять знания к решению задач Многогранники. Вершины, ребра, грани многогранника. Развертка. Многогранные углы. Выпуклые многогранники. Теорема Эйлера. Призма, ее основания, боковые ребра, высота, боковая поверхность. Прямая и наклонная призма. Правильная призма. Параллелепипед. Куб. Пирамида, ее основание, боковые ребра, высота, боковая поверхность. Треугольная пирамида. Правильная пирамида. Усеченная пирамида. Симметрии в кубе, в параллелепипеде, в призме и пирамиде. Понятие о симметрии в пространстве (центральная, осевая, зеркальная). Примеры симметрий в окружающем мире. Сечения куба, призмы, пирамиды. Представление о правильных многогранниках (тетраэдр, куб, октаэдр, додекаэдр и икосаэдр). Требования к уровню подготовки учеников 10 класса уметь · распознавать на чертежах и моделях пространственные формы; соотносить трехмерные объекты с их описаниями, изображениями; · описывать взаимное расположение прямых и плоскостей в пространстве, аргументировать свои суждения об этом расположении; · анализировать в простейших случаях взаимное расположение объектов в пространстве; · изображать основные многогранники и круглые тела; выполнять чертежи по условиям задач; · строить простейшие сечения куба, призмы, пирамиды; · решать планиметрические и простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей, объемов); · использовать при решении стереометрических задач планиметрические факты и методы; · проводить доказательные рассуждения в ходе решения задач; использовать приобретенные знания и умения в практической деятельности и повседневной жизни для: · исследования (моделирования) несложных практических ситуаций на основе изученных формул и свойств фигур; · вычисления объемов и площадей поверхностей пространственных тел при решении практических задач, используя при необходимости справочники и вычислительные устройства. Критерии и нормы оценки знаний, умений и навыков обучающихся по математике. 1. Оценка письменных контрольных работ обучающихся по математике. Ответ оценивается отметкой «5», если: работа выполнена полностью; в логических рассуждениях и обосновании решения нет пробелов и ошибок; в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала). Отметка «4» ставится в следующих случаях: работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки); допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки). Отметка «3» ставится, если: допущено более одной ошибки или более двух – трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме. Отметка «2» ставится, если: допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере. Отметка «1» ставится, если: работа показала полное отсутствие у обучающегося обязательных знаний и умений по проверяемой теме или значительная часть работы выполнена не самостоятельно. Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий. 2.Оценка устных ответов обучающихся по математике Ответ оценивается отметкой «5», если ученик: полно раскрыл содержание материала в объеме, предусмотренном программой и учебником; изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности; правильно выполнил рисунки, чертежи, графики, сопутствующие ответу; показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания; продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков; отвечал самостоятельно, без наводящих вопросов учителя; возможны одна – две неточности при освещение второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя. Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков: в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа; допущены один – два недочета при освещении основного содержания ответа, исправленные после замечания учителя; допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя. Отметка «3» ставится в следующих случаях: неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала (определены «Требованиями к математической подготовке обучающихся» в настоящей программе по математике); имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя; ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме; при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков. Отметка «2» ставится в следующих случаях: не раскрыто основное содержание учебного материала; обнаружено незнание учеником большей или наиболее важной части учебного материала; допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя. Отметка «1» ставится, если: ученик обнаружил полное незнание и непонимание изучаемого учебного материала или не смог ответить ни на один из поставленных вопросов по изученному материалу. Общая классификация ошибок. При оценке знаний, умений и навыков обучающихся следует учитывать все ошибки (грубые и негрубые) и недочёты. 3.1. Грубыми считаются ошибки: - незнание определения основных понятий, законов, правил, основных положений теории, незнание формул, общепринятых символов обозначений величин, единиц их измерения; - незнание наименований единиц измерения; - неумение выделить в ответе главное; - неумение применять знания, алгоритмы для решения задач; - неумение делать выводы и обобщения; - неумение читать и строить графики; - неумение пользоваться первоисточниками, учебником и справочниками; - потеря корня или сохранение постороннего корня; - отбрасывание без объяснений одного из них; - равнозначные им ошибки; - вычислительные ошибки, если они не являются опиской; - логические ошибки. 3.2. К негрубым ошибкам следует отнести: - неточность формулировок, определений, понятий, теорий, вызванная неполнотой охвата основных признаков определяемого понятия или заменой одного - двух из этих признаков второстепенными; - неточность графика; - нерациональный метод решения задачи или недостаточно продуманный план ответа (нарушение логики, подмена отдельных основных вопросов второстепенными); - нерациональные методы работы со справочной и другой литературой; - неумение решать задачи, выполнять задания в общем виде. 3.3. Недочетами являются: - нерациональные приемы вычислений и преобразований; - небрежное выполнение записей, чертежей, схем, графиков. Литература Пособия для учителя 1.Геометрия, 10-11: Учеб. для общеобразовательных учреждений/ Л.С. Атанасян, В.Ф. Бутузов, С. Б. Кадомцев и др.-Москва: Просвещение, 2009 год 2.Ершова А.П., Голобородько В.В., Ершова А.С. Самостоятельные и контрольные работы по геометрии для 10 класса.- 4-е издание, испр. и доп.- М.:Илекса, 2007,- 175 с. 3.Геометрия. 10-11 классы: тесты для текущего и обобщающего контроля/авт.сост.Г.И.Ковалёва, Н.И.Мазурова.- Волгоград: Учитель, 2009, 187 стр. 4.Виртуальная школа Кирилла и Мефодия. Репетитор по математике. Москва. 2007 год 5. Учебное электронное издание. Математика 5- 11 класссы. Практикум. Под редакцией Дубровского В.Н., 2004. 6.Экспресс- подготовка к экзамену. 9-11 классы. Математика. Быстрое усвоение курса. Конспекты уроков. Тренажёр НГЭ. Новая школа, 2006год 7. Сдаём ЕГЭ по математике. Интерактивные контрольные измерительные материалы. Москва. Фирма «1С» 8. Интерактивный курс подготовки к ЕГЭ. Математика. Москва. Фирма «1С» 9. Интерактивный тренинг- подготовка к ЕГЭ. Математика, Москва, 2007 год 10.Единый государственный экзамен: математика: контрольные измерительные материалы: 2010.- М.Просвещение, СПб: филиал издательства «Просвещение» 11. Яровенко В.А. Поурочные разработки по геометрии: 10 класс. М.:ВАКО, 2006.- 303 с. Пособия для учащихся 1. Геометрия, 10-11. Л.С.Атанасян, В.Ф.Бутузов, С.В.Кадомцев и др. -М.: Просвещение, 2008. 2. Зив Б.Г. Дидактические материалы по геометрии для 11 класса. -М.: Дрофа, 2004 Дополнительная литература: * Денищева А.О. Единый государственный экзамен.