Вариант 9-12 - Школа 26 Иркутск

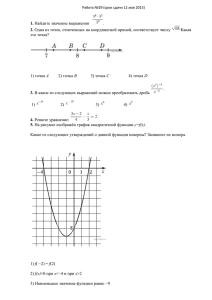
Пояснения
Ответы
Ключ PDF-версия
9
Вариант № 39418
1. B 1 № 136. Найдите значение выражения
Решение.
Последовательно получаем:
Ответ: −820.
2. A 1 № 311303. Известно, что
1)
2)
3)
4)
Решение.
. Какое из указанных утверждений неверно?
Рассмотрим все варианты ответа:
— верно, поскольку
1)
— верно,
2)
— неверно,
3)
4)
— верно.
Правильный ответ указан под номером 3.
3. A 2 № 137277. Найдите значение выражения:
1) 3200000
2) 0,00032
3) 0,000032
4) 0,0000032
Решение.
Перепишем выражение и сгруппируем сомножители:
.
Правильный ответ указан под номером 3.
4. B 2 № 311393. Решите уравнение
.
Если корней несколько, запишите их через точку с запятой в порядке возрастания.
Решение.
Используем свойство пропорции:
О т в е т : 24.
5. B 3 № 138. Установите соответствие между графиками функций и формулами, которые
их задают.
1)
2)
3)
4)
Ответ укажите в виде последовательности цифр без пробелов и запятых в указанном
порядке.
А Б В
Решение.
Определим вид графика каждой из функций:
уравнение прямой c точкой пересечения
1)
с осью ординат
2)
уравнение гиперболы.
3)
уравнение параболы, ветви которой направленны вверх.
4)
уравнение прямой c точкой пересечения
с осью ординат
Тем самым найдено соответствие: A — 4, Б — 3, В — 2.
О т в е т : 432.
6. @@@@B 4 № 137307. Последовательность задана условиями
дите .
Решение.
,
. Най-
Найдём несколько первых членов последовательности:
Отсюда ясно, что все члены последовательности с нечётными номерами равны 4.
О т в е т : 4.
Примечание.
Из рекуррентной формулы, задающей n-й член последовательности, можно непосредственно получить, что
Отсюда ясно, что все члены последовательности с нечётными номерами равны первому
члену последовательности, а все члены последовательности с чётными равны второму
члену последовательности.
7. B 5 № 311453. Упростите выражение
и найдите его значение
при
. В ответе запишите найденное значение.
Решение.
Упростим выражение:
При
, значение полученного выражения равно 26:5 = 5,2.
Ответ: 5,2.
8. A 3 № 311949. Решите систему неравенств
На каком из рисунков изображено множество её решений?
1) 1)
2) 2)
3) 3)
4) 4)
Решение.
Решим систему:
Правильный ответ указан под номером 3.
9. B 6 № 311680.
В равнобедренном треугольнике ABC с основанием AC внешний угол при вершине C
равен 123°. Найдите величину угла ABC. Ответ дайте в градусах.
Решение.
Углы ACB и ABC равны, т. к. находятся при основании равнобедренного треугольника;
назовём один из них буквой . По свойству треугольника, ∠ABC = 180° − − . Угол BCA
смежен с углом 123°, значит, равен 180° − 123° = 57°, а значит, = 57°. ∠ABC = 180° −
2·57° = 66°.
Ответ: 66.
10. B 7 № 311479.
Прямоугольный треугольник с катетами 5
см и 12 см вписан в окружность. Чему равен радиус этой окружности?
Решение.
Пусть R-радиус описанной окружности. Так как окружность описана вокруг прямоугольного треугольника, то ее центр лежит на середине гипотенузы. Таким образом, гипотенуза
равна 2R.
По теореме Пифагора имеем:
11. B 8 № 311761. Найдите площадь прямоугольника, если его периметр равен 44 и одна
сторона на 2 больше другой.
Решение.
Площадь прямоугольника равна произведению его сторон. Найдём стороны прямоугольника. Пусть x — меньшая сторона прямоугольника. Тогда периметр прямоугольника
равен
откуда
Поэтому площадь прямоугольника
равна
Ответ: 120.
12. B 9 № 66.
ражённого на рисунке.
Решение.
Найдите тангенс угла А треугольника ABC, изоб-
Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к
прилежащему:
О т в е т : 0,4.
13. B 10 № 311959. Укажите номера верных утверждений.
1) В любую равнобедренную трапецию можно вписать окружность.
2) Диагональ параллелограмма делит его углы пополам.
3) Площадь прямоугольного треугольника равна половине произведения его катетов.
Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
Решение.
Утверждение (2) неверно: диагональ параллелограмма делит его углы пополам только в
том случае, когда параллелограмм является ромбом. Утверждение (1) неверно, так как не
в любую равнобедренную трапецию можно вписать окружность.
Утверждение (3) верно.
О т в е т : 3.
14. A 4 № 311297.
Завуч школы подвел итоги по
выбору предметов для сдачи ЕГЭ учащимися 11-х классов. Результаты представлены на
диаграмме. Сколько примерно учащихся выбрали для сдачи ЕГЭ физику?
1) 16
2) 12
3) 14
4) 8
Решение.
На диаграмме физике соответствует второй столбец. Видно, что физику сдавало больше
12, но меньше 16 человек. Таким образом, наиболее подходящий вариант ответа — 14 человек.
Правильный ответ указан под номером 3.
15. B 11 № 94. На рисунке изображён график изменения атмосферного давления в городе
Энске за три дня. По горизонтали указаны дни недели, по вертикали — значения атмосферного давления в миллиметрах ртутного столба. Укажите наибольшее значение атмо-
сферного давления во вторник.
Решение.
Цена деления шкалы давления: 2 мм рт. ст. Наибольшее значение давления
ник равно
мм рт. ст. плюс половина цены деления шкалы давления:
О т в е т : 755.
во втор-
16. B 12 № 137258. Какая сумма (в рублях) будет проставлена в кассовом чеке, если стоимость товара 520 р., и покупатель оплачивает его по дисконтной карте с 5%-ной скидкой?
Решение.
Рассчитаем скидку, которую получает покупатель оплачивая товар по дисконтной карте с
5%-ной скидкой:
руб. Таким образом, итоговая цена со скидкой равна:
руб.
О т в е т : 494.
17. B 13 № 70.
От столба высотой 9 м к дому натянут провод, который крепится на высоте 3 м от земли (см. рисунок). Расстояние от дома до столба
8 м. Вычислите длину провода.
Решение.
Проведём отрезок, параллельный горизонтальной прямой, как показано на рисунке. Таким образом задача сводится к нахождению гипотенузы
прямоугольного треугольника; обозначим её за . По теореме Пифагора, гипотенуза ищется следующим образом:
О т в е т : 10.
18. B 14 № 311906. В математические кружки города ходят школьники 5–8 классов. Распределение участников математических кружков представлено в круговой диаграмме.
Какое утверждение относительно участников кружков верно, если всего их посещают 354
школьника?
1) в кружки не ходят пятиклассники
2) восьмиклассников ходит больше, чем семиклассников
3) больше половины участников кружков учатся не в седьмом классе
4) шестиклассников меньше 88 человек
Решение.
Проанализируем каждое утверждение.
Утверждение 1) неверно: пятиклассники занимаются в кружках.
Утверждение 2) не верно: семиклассников больше, чем восьмиклассников.
Утверждение 3) верно: семиклассников меньше половины всех учащихся, значит, не семиклассников больше половины всех учащихся.
Утверждение 4) неверно. Шестиклассников больше четверти всех учащихся, т. е. больше
354 : 4 = 88,5 человек.
Таким образом, верно третье утверждение.
19. B 15 № 311486. Какова вероятность того, что случайно выбранное натуральное число
от 192 до 211 включительно делится на 5?
Решение.
Всего чисел - 20 штук. Из них 4 делятся на 5. Таким образом,вероятность того, что случайно выбранное натуральное число от 192 до 211 включительно делится на 5 равна 0,2.
20. B 16 № 311542. Чтобы перевести значение температуры по шкале Цельсия (t °C) в
шкалу Фаренгейта ( °F) пользуются формулой
, где — градусы Цельсия,
— градусы Фаренгейта. Какая температура (в градусах) по шкале Фаренгейта соответствует 20° по шкале Цельсия?
Решение.
Подставим значение температуры в формулу :
О т в е т : 68.
21. C 1 № 177. Решите неравенство
Решение.
Перенесём две части неравенства в одну часть и избавимся от знаменателя:
приравняем левую часть к нулю и найдём корни. Отсюда
и
Расставив корни на координатной прямой, определим знаки неравенства, получаем:
О т в е т : (-0,75; 3).
22. C 2 № 311658. Кролик утверждает, что вчера Винни-Пух съел не менее 9 баночек
мёда, Пятачок — что не менее 8 баночек, ослик Иа — что не менее 7. Сколько баночек
мёда съел вчера Винни-Пух, если из трех этих утверждений истинно только одно?
Решение.
Если прав Кролик, то правы и Пятачок, и Иа, а этого не может быть, т.к. истинно только
одно утверждение. Аналогично: если прав Пятачок, то Иа тоже прав, получили два истинных утверждения, а должно быть только одно. Значит, во-первых, Пятачок неправ, и Пух
съел менее 8 баночек. Во-вторых, прав может быть только Иа, потому что один из них
должен быть прав. Следовательно, Пух съел не менее 7 баночек. Единственное целое
число, которое не меньше 7, но меньше 8 — это число 7.
23. C 3 № 311611. Постройте график функции
ния , при которых прямая
имеет с ним ровно две общие точки.
Решение.
и найдите значе-
Раскрывая модули, получаем, что график функции совпадает с прямой
, совпадает с прямой
при
и совпадает с прямой
График изображен на рисунке.
Прямая
имеет с графиком данной функции ровно две общие точки при
.
Ответ:
при
при
.
и
.
24. C 4 № 311262. Стороны
,
,
треугольника
равны
,
и соотвественно. Точка расположена вне треугольника
, причем отрезок
пересекает отрезок
в точке, отличной от . Известно, что треугольник с вершинами , и подобен исходному. Найдите косинус угла
, если
> 90°.
Решение.
По условию
> 90°, тогда треугольник
KAC является тупоугольным. Так как треугольник KAC подобен ABC, то ABC является
также тупоугольным.
Определим соответствующие углы. Так как напротив большего угла лежит большая сторона, то
> 90°, тогда
Так как
, то
и
.
Треугольники ABC и CAK подобны. Имеем:
таким образом,
,
По теореме косинусов в треугольнике AKC имеем:
Подставляя получаем,
Ответ:
25. C 5 № 311665. Докажите, что у равных треугольников
ведённые из вершины и , равны.
Решение.
и
биссектрисы, про-
Пусть
и
— биссектрисы треугольников
и
. В треугольниках
и
соответственно равны стороны
и
, а также углы и ,
и
. Следовательно, треугольники равны по второму признаку равенства треугольников. Значит,
, что и требовалось доказать.
26. C 6 № 130. Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 8, тангенс угла BAC равен . Найдите радиус вписанной окружности треугольника ABC.
Решение.
Угол BAC равен углу BCP так как
и
. Так как тангенс это отношение противолежащего катета к прилежащему, имеем:
Тогда BP=4x, PC=3x, а гипотенуза BC=5x по теореме Пифагора. Площадь треугольника равна произведению половины его периметра на
радиус вписанной окружности, но площадь прямоугольного треугольника равна половине
произведения катетов, имеем:
Таким образом, BP=16, PC=12, а BC=20. Так как
реме Пифагора.
то AC=15, а AB=25 по тео-
В треугольнике ABC площадь равна произведению половины его периметра на радиус
вписанной в него окружности, но площадь прямоугольного треугольника равна половине
произведения катетов, имеем:
О т в е т : r=5
10
Пояснения
Ответы
Ключ PDF-версия
Вариант № 39419
1. B 1 № 287934. Расположите в порядке возрастания:
1)
2)
3)
Решение.
4)
Поскольку:
;
получаем:
Правильный ответ указан под номером 2.
2. A 1 № 205775. Какое из следующих неравенств не следует из неравенства
1)
2)
3)
4)
Решение.
Приведем исходное неравенство соотвествующему виду:
1)
2)
3)
4)
?
Неравенство
не следует из исходного неравенства.
Правильный ответ указан под номером 2.
3. A 2 № 137272. Найдите значение выражения
.
1)
2)
3)
4) 4
Решение.
Последовательно получаем:
Правильный ответ указан под номером 1.
4. B 2 № 311755. Решите уравнение
Решение.
Умножим левую и правую часть уравнения на 4, получаем:
Ответ: −20.
5. B 3 № 311339. Укажите соответствие между графиками функций и формулами, которые
их задают.
1)
2)
3)
4)
Ответ укажите в виде последовательности цифр без пробелов и запятых в указанном
порядке
А Б В
Решение.
Определим вид графика каждой из функций.
1)
точке −2.
уравнение прямой, которая пересекает ось абсцисс в точке 2 ; ось ординат в
2)
уравнение степенной функции с положительным дробным показателем.
График проходит через точку (1; 0).
3)
уравнение параболы, ветви которой направлены вверх.
4)
уравнение степенной функции с положительным дробным показателем.
График проходит через точку (−1; 0).
Таким образом, искомое соответствие: A — 4, Б — 3, В — 1.
Ответ: 431.
6. B 4 № 139. Дана арифметическая прогрессия
десяти её членов.
Решение.
Найдите сумму первых
Определим разность арифметической прогрессии:
Сумма первых k-ых членов может быть найдена по формуле
Необходимо найти
, имеем:
О т в е т : 75.
7. B 5 № 311452. Упростите выражение
и найдите его значение
при
. В ответе запишите найденное значение.
Решение.
Упростим выражение:
При
, значение полученного выражения равно 19:2 = 9,5.
Ответ: 9,5.
8. A 3 № 107. Решите неравенство
ражено множество его решений.
и определите, на каком рисунке изоб-
1)
2)
3)
4)
Решение.
Решим неравенство:
Решение неравенства изображено на рис. 1.
Правильный ответ указан под номером 1.
9. B 6 № 132776. Сумма двух углов равнобедренной трапеции равна
ший угол трапеции. Ответ дайте в градусах.
Решение.
. Найдите боль-
Так как трапеция является равнобедренной, то углы при основании равны
трапеции параллельны, таким образом, так как сумма смежных углов равна
угол равен
. Основания
больший
10. B 7 № 311510. В угол величиной 70° вписана окружность, которая касается его сторон
в точках
и . На одной из дуг этой окружности выбрали точку
так, как показано
на рисунке. Найдите величину угла
Решение.
.
По свойству касательных , проведенных из одной точки, отрезки DA и DB - равны. Таким
образом, треугольник DAB- равнобедренный. Угол DAB равен
Проведем радиус OB.
Угол OBD - прямой, так как касательная к окружности перпендикулярна радиусу, проведенному в точку касания. Тогда
Треугольник OAB - равнобедренный, таким образом,
Угол AOB-центральный и опирается на дугу AB. Угол
ACB - вписанный и опирается также на дугу AB. Таким образом,
Ответ: 55.
11. B 8 № 169902. В ромбе сторона равна 10, одна из диагоналей —
щий напротив этой диагонали, равен
Решение.
, а угол, лежа-
. Найдите площадь ромба деленную на
Площадь ромба равна произведению сторон на синус угла между ними, имеем:
О т в е т : 50.
Примечание:
Можно найти вторую диагональ по теореме косинусов и вычислить площадь ромба как
половина произведения диагоналей.
---------В открытом банке иррациональный ответ.
12. B 9 № 311333.
нок, найдите
Решение.
На рисунке изображен ромб
. Используя рису-
.
Так как OBC- прямоугольный треугольник, то
. Таким образом,
Ответ: 0,75.
13. B 10 № 169930. Какие из следующих утверждений верны?
1) Окружность имеет бесконечно много центров симметрии.
2) Прямая не имеет осей симметрии.
3) Правильный пятиугольник имеет пять осей симметрии.
4) Квадрат не имеет центра симметрии.
Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
Решение.
Проверим каждое из утверждений.
1) «Окружность имеет бесконечно много центров симметрии.»— неверно, плоская фигура
обладает
центральной симметрией, если она симметрична сама себе относительно центра
2) «Прямая не имеет осей симметрии.» — неверно, прямая имеет бесконечное число осей
симметрии.
3) «Правильный пятиугольник имеет пять осей симметрии.» — верно, каждая ось симметрии любого правильного многоугольника с нечетным числом сторон проходит через вершину и середину противоположной стороны.
4) «Квадрат не имеет центра симметрии.» — неверно, центр симметрии квадрата является
точка пересечения диагоналей.
14. A 4 № 56. Учёный Иванов выезжает из Москвы на конференцию в Санкт-Петербургский университет. Работа конференции начинается в 10:00. В таблице дано расписание
ночных поездов Москва — Санкт-Петербург.
Номер поезда Отправление из Москвы Прибытие в Санкт-Петербург
026A
23:00
06:30
002A
23:55
07:55
038A
00:44
08:48
016A
01:00
08:38
Путь от вокзала до университета занимает полтора часа. Укажите номер самого позднего
(по времени отправления) из московских поездов, которые подходят учёному Иванову.
1) 026A
2) 002A
3) 038A
4) 016A
Решение.
Поскольку путь от вокзала до университета занимает полтора часа, поезд должен прибыть
на вокзал не позднее 08:30. Этому условию удовлетворяют поезда под номерами: 026А и
002А. Из них позже отправляется поезд под номером 002А.
Правильный ответ указан под номером 2.
15. B 11 № 94. На рисунке изображён график изменения атмосферного давления в городе
Энске за три дня. По горизонтали указаны дни недели, по вертикали — значения атмосферного давления в миллиметрах ртутного столба. Укажите наибольшее значение атмо-
сферного давления во вторник.
Решение.
Цена деления шкалы давления: 2 мм рт. ст. Наибольшее значение давления
ник равно
мм рт. ст. плюс половина цены деления шкалы давления:
во втор-
О т в е т : 755.
16. B 12 № 137263. Число хвойных деревьев в парке относится к числу лиственных как
1:4. Сколько процентов деревьев в парке составляют лиственные?
Решение.
Всего деревьев пять частей, из них лиственных — четыре части. это составляет 4 : 5 = 0,8
или 80 %.
Ответ: 80.
---------Дублирует задание 137250.
17. B 13 № 96.
От столба к дому натянут провод длиной 10 м,
который закреплён на стене дома на высоте 3 м от земли (см. рисунок). Вычислите высоту
столба, если расстояние от дома до столба равно 8 м.
Решение.
Искомую сторону обозначим за . Проведём отрезок, параллельный горизонтальной прямой, как показано на рисунке;
— катет получившегося
прямоугольного треугольника. По теореме Пифагора, катет ищется следующим образом:
Найдём искомую сторону:
О т в е т : 9.
18. B 14 № 206050. На диаграмме показано распределение земель Уральского, Приволжского, Южного и Дальневосточного Федеральных округов по категориям. Определите по
диаграмме, в каком округе доля земель сельскохозяйственного назначения наименьшая.
*прочее — это земли поселений; земли промышленности и иного специального назначения; земли особо охраняемых территорий и объектов.
Варианты ответа
1) УРАЛЬСКИЙ ФО
2) ПРИВОЛЖСКИЙ ФО
3) ЮЖНЫЙ ФО
4) ДАЛЬНЕВОСТОЧНЫЙ ФО
Решение.
Из диаграмм видно, что наименьшая доля земель сельскохозяйственного назначения в
Дальневосточном ФО. Таким образом, верный ответ указан под номером 4.
19. B 15 № 311512. В группе из 20 российских туристов несколько человек владеют иностранными языками. Из них пятеро говорят только по-английски, трое только по-французски, двое по-французски и по-английски. Какова вероятность того, что случайно выбранный турист говорит по-французски?
Решение.
Количество туристов, говорящих по-французски, равно 5. Поэтому вероятность того, что
случайно выбранный турист говорит по-французски равна
20. B 16 № 311533. В фирме «Чистая вода» стоимость (в рублях) колодца из железобетонных колец рассчитывается по формуле
, где — число колец, установленных при рытье колодца. Пользуясь этой формулой, рассчитайте стоимость колодца
из 11 колец.
Решение.
Подставим количество колец в формулу для расчета стоимости. Имеем:
О т в е т : 50 500.
21. C 1 № 311236. Разложите на множители:
Решение.
.
Имеем:
Ответ:
.
22. C 2 № 311600. Расстояние между городами А и В равно 750 км. Из города А в город В
со скоростью 50 км/ч выехал первый автомобиль, а через три часа после этого навстречу
ему из города В выехал со скоростью 70 км/ч второй автомобиль. На каком расстоянии от
города А автомобили встретятся?
Решение.
За первые три часа пути автомобиль, выехавший из города А, проехал 150 километров и
расстояние от него до города. В стало равным 600 км. Далее, скорость сближения двух автомобилей равна 120 км/ч, значит, они встретятся через 5 часов после выезда второго автомобиля. Таким образом, первый автомобиль до встречи находился в пути 8 часов, и проехал за это время 400 километров.
Ответ: 400 км.
23. C 3 № 311619. Постройте график функции
и определите, при каких значениях прямая
Решение.
имеет с графиком ровно две общие точки.
График функции состоит из двух лучей и отрезка.
На рисунке видно, что график
имеет ровно две общих точки с горизонтальными прямыми
и
.
Ответ: 1; −2.
24. C 4 № 50. В прямоугольном треугольнике
,
Решение.
. Найдите медиану
с прямым углом
этого треугольника.
известны катеты:
Медиана, проведенная к гипотенузе, равна её половние:
О т в е т : 5.
25. C 5 № 311606. Два равных прямоугольника имеют общую вершину
жите, что площади треугольников
и
равны.
(см. рис.). Дока-
Решение.
Две стороны одного треугольника соответственно равны двум сторонам другого:
и
. Рассмотрим углы между ними:
360°
180°
.
Поэтому
.
26. C 6 № 311703. Длина катета
прямоугольного треугольника
равна 8 см. Окружность с диаметром
пересекает гипотенузу
в точке . Найдите площадь треугольника
, если известно, что
.
Решение.
Пусть
см,
см. По теореме Пифагора:
потенуза
см и
.
По теореме о секущей и касательной
.
Следовательно,
, откуда
.
Тогда
.
Следовательно, площадь треугольника равна
.
Ответ:
.
11
Пояснения
Ответы
Ключ PDF-версия
Вариант № 39420
1. B 1 № 287936. Расположите в порядке возрастания:
1)
2)
3)
Решение.
4)
см. Поэтому ги-
Запишем заданные числовые выражения в виде десятичных дробей:
Заметим, что
4.
Поэтому верный вариант ответа указан по номером
2. A 1 № 311380. Одна из точек, отмеченных на координатной прямой, соответствует
числу
Какая это точка?
1) A
2) B
3) C
4) D
Решение.
Приведём все дроби к одному знаменателю. Получим:
Поскольку
точка С соответствует числу
Правильный ответ указан под номером 3.
3. A 2 № 137280. Найдите значение выражения
1) −125
2) 125
при
.
3)
4)
Решение.
Упростим выражение используя формулы
,
и
:
Подставим значение :
О т в е т : 2.
4. B 2 № 311907. Решите уравнение −2(5 − 3x) = 7x + 3.
Решение.
Последовательно получаем:
О т в е т : −13.
5. B 3 № 193093. На одном из рисунков изображен график функции
жите номер этого рисунка.
1)
2)
. Ука-
3)
4)
Решение.
Коэффициент
, поэтому ветви параболы направлены вверх. Абсцисса вершины пара-
болы равна:
Правильный вариант ответа указан под номером 1.
6. B 4 № 311909. Арифметическая прогрессия задана условиями:
. Найдите сумму первых 19 её членов.
Решение.
Сумма n первых членов арифметической прогрессии даётся формулой
По условию,
О т в е т : 95.
откуда получаем
7. B 5 № 311408. Представьте в виде дроби выражение
ние при
. В ответ запишите полученное число.
Решение.
и найдите его значе-
Упростим выражение:
Найдем значение выражения при
Ответ: −10.
8. A 3 № 311397. На каком рисунке изображено множество решений неравен-
ства
1)
2)
3)
4)
Решение.
Решим неравенство:
Множество решений неравенства изображено на рис. 4.
Правильный ответ указан под номером 4.
9. B 6 № 311412.
равны. Найдите угол
Решение.
Углы, отмеченные на рисунке одной дугой,
. Ответ дайте в градусах.
Углы 1 и 2 равны как вертикальные. Таким образом,
Ответ: 40.
10. B 7 № 311331.
дуг
и
равны 150° и 68° соответственно.
Решение.
Найдите
, если градусные меры
Так как вписанный угол равен половине дуги на которую он опирается, имеем
,а
. В треугольнике EFD ,
11. B 8 № 143.
ражённой на рисунке.
Решение.
.
Найдите площадь трапеции, изоб-
Площадь трапеции( ) ищется путём перемножения длины высоты и средней линии(среднего арифметического двух оснований). В данной трапеции длина средней линии равна
, а длина высоты — 6, таким образом, площадь трапеции равна:
Ответ: 36.
12. B 9 № 311400.
На клетчатой бумаге с размером клетки
1см × 1см изображён параллелограмм. Найдите длину его большей высоты. Ответ дайте в
сантиметрах.
Решение.
По рисунку видно, что длина большей высоты параллелограмма равна 5 см.
Ответ: 5.
13. B 10 № 169921. Какие из следующих утверждений верны?
1) Если расстояние между центрами двух окружностей равно сумме их диаметров, то эти
окружности касаются.
2) Вписанные углы окружности равны.
3) Если вписанный угол равен
равна
.
, то дуга окружности, на которую опирается этот угол,
4) Через любые четыре точки, не принадлежащие одной прямой, проходит единственная
окружность.
Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
Решение.
Проверим каждое из утверждений.
1) «Если расстояние между центрами двух окружностей равно сумме их диаметров, то эти
окружности касаются.» — неверно, если расстояние между центрами двух окружностей
равно сумме их радиусов, то эти окружности касаются.
2) «Вписанные углы окружности равны.» — неверно, угол, вершина которого лежит на
окружности, а стороны пересекают окружность, называется вписанным углом. Они равны
тогда, когда опираются на одну и ту же дугу.
3) «Если вписанный угол равен
, то дуга окружности, на которую опирается этот угол,
равна
.» — верно, вписанный угол измеряется половиной дуги, на которую он опирается.
4) «Через любые четыре точки, не принадлежащие одной прямой, проходит единственная
окружность.» — неверно, некоторые точки могут не попасть на окружность.
14. A 4 № 311291. Дорожный знак, изображённый на рисунке, называется «Ограничение
длины». Его устанавливают там, где запрещён проезд транспортного средства, габариты
которого (с грузом или без груза) превышают установленную длину.
Какому из данных транспортных средств этот знак запрещает проезд?
1) бензовозу длиной 7600 мм
2) автомобилю Газель длиной 6330 мм
3) автотопливозаправщику длиной 10 200 мм
4) автоцистерне длиной 8250 мм
Решение.
Переведем допустимую длину в миллиметры: 10 м = 10 000 мм и сравним с предложенными вариантами:
1) 7600 < 10000 — проезд разрешен.
2) 6330 < 10000 — проезд разрешен.
3) 10200 > 10000 — проезд запрещен.
4) 8250 < 10000 — проезд разрешен.
Таким образом, знак «Ограничение длины» запрещает проезд автотопливозаправшику.
Правильный ответ указан под номером 3.
15. B 11 № 198. На рисунке изображён график изменения атмосферного давления в городе
Энске за три дня. По горизонтали указаны дни недели, по вертикали — значения атмосферного давления в миллиметрах ртутного столба. Укажите наибольшее значение атмо-
сферного давления во вторник.
Решение.
Цена деления шкалы давления: мм рт. ст. Минимальное значение давления
ник равно
мм рт. ст. плюс половина цены деления шкалы давления:
во втор-
О т в е т : 755.
16. B 12 № 137249. На пост председателя школьного совета претендовали два кандидата.
В голосовании приняли участие 120 человек. Голоса между кандидатами распределились
в отношении 3:5. Сколько голосов получил победитель?
Решение.
Пусть x голосов приходится на одну часть, тогда приходится на второго кандидата, а
— на первого. Зная, что в голосовании участвовало 120 человек составим уравнение:
голосов.
Таким образом, победитель получил:
голосов.
О т в е т : 75.
17. B 13 № 132767. Найдите периметр прямоугольного участка земли, площадь которого
равна 800 м2 и одна сторона в 2 раза больше другой. Ответ дайте в метрах.
Решение.
Пусть x-длина одной стороны, тогда длина второй стороны 2x. Так как площадь прямоугольника равна произведению его смежных сторон, имеем:
Периметр прямоугольника - сумма длин всех его сторон. Таким образом,
О т в е т : 120.
18. B 14 № 206050. На диаграмме показано распределение земель Уральского, Приволжского, Южного и Дальневосточного Федеральных округов по категориям. Определите по
диаграмме, в каком округе доля земель сельскохозяйственного назначения наименьшая.
*прочее — это земли поселений; земли промышленности и иного специального назначения; земли особо охраняемых территорий и объектов.
Варианты ответа
1) УРАЛЬСКИЙ ФО
2) ПРИВОЛЖСКИЙ ФО
3) ЮЖНЫЙ ФО
4) ДАЛЬНЕВОСТОЧНЫЙ ФО
Решение.
Из диаграмм видно, что наименьшая доля земель сельскохозяйственного назначения в
Дальневосточном ФО. Таким образом, верный ответ указан под номером 4.
19. B 15 № 311501. На экзамене 25 билетов, Сергей не выучил 3 из них. Найдите вероятность того, что ему попадётся выученный билет.
Решение.
Сергей выучил 25-3=22 билета. Таким образом вероятность того, что ему попадётся выученный билет равна
20. B 16 № 311539. За 20 мин велосипедист проехал 7 км. Сколько километров он проедет
за t мин, если будет ехать с той же скоростью? Запишите соответствующее выражение.
Решение.
За 1 минуту велосипедист проезжает в 20 раз меньшее расстояние или
чит, за t минут он проедет 0,35t км.
км. Зна-
21. C 1 № 311255. Упростите выражение
Решение.
Имеем:
Ответ:
22. C 2 № 311770. Дима и Саша выполняют одинаковый тест. Дима отвечает за час на 12
вопросов теста, а Саша — на 22. Они одновременно начали отвечать на вопросы теста, и
Дима закончил свой тест позже Саши на 75 минут. Сколько вопросов содержит тест?
Решение.
Пусть x — количество вопросов теста через. Тогда получаем:
откуда находим x = 33 .
Ответ: 33
23. C 3 № 311571. Постройте график функции
и найдите все значения ,
при которых прямая
имеет с графиком данной функции ровно одну общую точку.
Решение.
Найдём область определения функции:
Значит, функция определена при
Поскольку
принимает вид
и
.
.
, получаем, что на области определения функция
.
График изображён на рисунке.
мая
имеет с графиком данной функции ровно одну общую точку при
Ответ:
Пря.
.
24. C 4 № 311698. Прямая, параллельная основаниям
и
трапеции
, проходит
через точку пересечения диагоналей трапеции и пересекает ее боковые стороны
и
в
точках и соответственно. Найдите длину отрезка
, если
,
.
Решение.
1)
по двум углам:
a)
как вертикальные;
б)
как внутренние накрест лежащие углы при
.
по двум углам:
2)
а)
и секущей
— общий;
б)
как соответственные углы при
и секущей
.
3)
4)
Ответ: 12 см.
25. C 5 № 103.
На стороне АС треугольника АВС выбраны точки D и E
так, что отрезки AD и CE равны (см. рисунок). Оказалось, что отрезки BD и BE тоже
равны. Докажите, что треугольник АВС — равнобедренный.
Решение.
Так как по условию BD=BE, то треугольник BDE является равнобедренным. Пусть угол
при основании этого треугольника равен x, тогда
Треугольники
BEC и BDA равны по двум сторонам и углу между ними, поэтому AB=BC и треугольник
ABC - равнобедренный.
26. C 6 № 311568. Три окружности, радиусы которых равны 2, 3 и 10, попарно касаются
внешним образом. Найдите радиус окружности, вписанной в треугольник, вершинами которого являются центры этих трёх окружностей.
Решение.
Стороны треугольника, вершинами которого
является центры этих трёх окружностей, равны 5, 12 и 13. Поскольку
, этот
треугольник прямоугольный. Площадь этого треугольника равна 30. В то же время, она
равна произведению радиуса вписанной окружности на полупериметр. Значит, искомый
радиус равен 30:
.
Ответ: 2.
Пояснения
Ответы
Ключ PDF-версия
12
Вариант № 39421
1. B 1 № 287935. Расположите в порядке убывания:
1)
2)
3)
Решение.
4)
Поскольку:
;
получаем:
Правильный ответ указан под номером 4.
2. A 1 № 205771. О числах и известно, что
выберите верные:
. Среди приведенных ниже неравенств
1)
2)
3)
1) Верно 1 и 2
2) Верно 2 и 3
3) Верно 1 и 3
4) Верно 1, 2 и 3
Решение.
Проверим все варианты ответа:
1)
— верно,
2)
— неверно,
3)
— верно.
Правильный ответ указан под номером 3.
3. A 2 № 137277. Найдите значение выражения:
1) 3200000
2) 0,00032
3) 0,000032
4) 0,0000032
Решение.
Перепишем выражение и сгруппируем сомножители:
.
Правильный ответ указан под номером 3.
4. B 2 № 311439. Решите уравнение
.
Если корней несколько, запишите их через точку с запятой в порядке возрастания.
Решение.
По теореме, обратной теореме Виета — сумма корней равна −2, а их произведение равно
−15
Тем самым, это числа −5 и 3.
О т в е т : −5; 3.
5. B 3 № 193091. Найдите значение по графику функции
на рисунке.
1)
2)
3)
изображенному
4)
Решение.
Абсцисса вершины параболы равна −1, поэтому
секает ось ординат в точке с ординатой 3, поэтому
Верный ответ указан под номером 4.
Ответ: 4.
откуда
Парабола пере-
6. B 4 № 137309. В первом ряду кинозала 30 мест, а в каждом следующем на 2 больше,
чем в предыдущем. Сколько мест в ряду с номером ?
Решение.
Количество мест в рядах кинозала образуют арифметическую прогрессию. По формуле
для нахождения n-го члена арифметической прогрессии имеем:
Ответ: 28+2n.
Ответ некорректный.
7. B 5 № 311463. Представьте в виде дроби выражение
ние при
. В ответ запишите полученное число.
Решение.
и найдите его значе-
Упростим выражение:
Найдем значение выражения при
:
Ответ: -5.
8. A 3 № 311397. На каком рисунке изображено множество решений неравен-
ства
1)
2)
3)
4)
Решение.
Решим неравенство:
Множество решений неравенства изображено на рис. 4.
Правильный ответ указан под номером 4.
9. B 6 № 132775. Один угол параллелограмма в два раза больше другого. Найдите меньший угол. Ответ дайте в градусах.
Решение.
Пусть x - меньший угол параллелограмма, а 2x - больший угол. У параллелограмма противоположные углы равны,
таким образом имеем уравнение:
Таким образом, меньший угол параллелограмма равен
10. B 7 № 311510. В угол величиной 70° вписана окружность, которая касается его сторон
в точках
и . На одной из дуг этой окружности выбрали точку
так, как показано
на рисунке. Найдите величину угла
Решение.
.
По свойству касательных , проведенных из одной точки, отрезки DA и DB - равны. Таким
образом, треугольник DAB- равнобедренный. Угол DAB равен
Проведем радиус OB.
Угол OBD - прямой, так как касательная к окружности перпендикулярна радиусу, проведенному в точку касания. Тогда
Треугольник OAB - равнобедренный, таким образом,
Угол AOB-центральный и опирается на дугу AB. Угол
ACB - вписанный и опирается также на дугу AB. Таким образом,
Ответ: 55.
11. B 8 № 169859. В треугольнике одна из сторон равна 12, другая равна 16, а синус угла
между ними равен . Найдите площадь треугольника.
Решение.
Площадь треугольника определяется по формуле половины произведения сторон на синус
угла между ними. Имеем:
О т в е т : 24.
12. B 9 № 311485.
те
.
Решение.
На квадратной сетке изображён угол
. Найди-
Опустим перпендикуляр BH. Треугольник ABH - прямоугольный. Таким образом,
Ответ: 3.
13. B 10 № 119. Укажите номера верных утверждений.
1) Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, делит основание на две равные части.
2) В любом прямоугольнике диагонали взаимно перпендикулярны.
3) Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу.
Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
Решение.
Проверим каждое из утверждений:
1) «Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, делит основание на две равные части» — верно, по свойству равнобедренного треугольника.
2) «В любом прямоугольнике диагонали взаимно перпендикулярны» — неверно, это
утверждение подходит исключительно для ромба, а не для прямоугольника.
3) «Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу»
— верно, т. к. окружность — множество точек, равноудаленных от одной(центра окружности).
О т в е т : 1; 3.
14. A 4 № 311296.
Фонд школьной библиотеки, состоящей из учебной и художественной литературы российских и зарубежных авторов, представлен в виде диаграммы. Сколько примерно книг учебной литературы в библиотеке,
если всего в библиотечном фонде 800 книг?
1) 400
2) 570
3) 300
4) 600
Решение.
Определим по диаграмме, какую долю книг в школьной библиотеке составляет учебная
литература. Эта доля будет равна доле площади круга, которая соответствует учебной литературе. Учебная литература иностранных авторов составляет книг, учебная литература
российских авторов составляет чуть меньше половины книг. Таким образом, суммарная
доля учебной литературы будет чуть меньше от общего количества книг (то есть немного меньше 600 книг) Таким образом, подходящий вариант ответа — 570 книг.
Правильный ответ указан под номером 2.
15. B 11 № 311357.
На рисунке изображен график полета тела, брошенного под углом к горизонту. По вертикальной оси откладывается расстояние от земли (в м), по горизонтальной оси — пройденный путь (в м). По рисунку определите, на какой высоте будет находиться тело в момент времени, когда оно пролетит 60
метров.
Решение.
По графику видно, что когда тело пролетит 60 метров, оно будет находиться на высоте 2
м.
Ответ: 2.
16. B 12 № 137250. Число хвойных деревьев в парке относится к числу лиственных как
1:4. Сколько процентов деревьев в парке составляют лиственные?
Решение.
Всего деревьев пять частей, из них лиственных — четыре части. это составляет 4 : 5 = 0,8
или 80 %.
О т в е т : 80.
17. B 13 № 311509. Глубина крепостного рва равна 8 м, ширина 5 м, а высота крепостной
стены от ее основания 20 м. Длина лестницы, по которой можно взобраться на стену, на 2
м больше, чем расстояние от края рва до верхней точки стены (см. рис.). Найдите длину
лестницы.
Решение.
Расстояние AB — гипотенуза прямоугольного треугольника с катетами 5 м и 20 − 8 = 12 м.
Тем самым, длина AB равна 13 м, а длина лестницы равна 15 м.
18. B 14 № 311314. 156 учащимся восьмых классов некоторой школы была предложена
контрольная работа по алгебре из 5 заданий. По результатам составили таблицу, в которой
указали число учащихся, выполнивших одно, два три и т.д. заданий:
Сколько человек получили оценку выше «3», если критерии выставления оценок определялись по таблице?
Решение.
По таблице мы видим, что оценку выше «3» получают учащиеся, выполнившие более трех
заданий.
Таким образом оценку выше «3» получили 12+37=49 учащихся.
Ответ: 49.
19. B 15 № 45. На тарелке лежат пирожки, одинаковые на вид: 4 с мясом, 8 с капустой и 3
с яблоками. Петя наугад выбирает один пирожок. Найдите вероятность того, что пирожок
окажется с яблоками.
Решение.
Пирожков с яблоками 3, а всего пирожков 15. Поэтому вероятность того, что Петя возьмёт
пирожок с яблоками равна
О т в е т : 0,2.
20. B 16 № 311768. Чтобы перевести значение температуры по шкале Цельсия (t °C) в
шкалу Фаренгейта (t °F), пользуются формулой F = 1,8C + 32 , где C — градусы Цельсия,
F — градусы Фаренгейта. Какая температура по шкале Фаренгейта соответствует 111° по
шкале Цельсия?
Решение.
Подставим в формулу значение переменной
:
О т в е т : 231,8.
21. C 1 № 311243. Сократите дробь
Решение.
Корни квадратного трехчлена
Имеем
Замечание. Учащийся может разложить трехчлен на множители каким-либо иным способом. Например:
Ответ:
22. C 2 № 311617. Чтобы накачать в бак 117 л воды, требуется на 5 минут больше времени, чем на то, чтобы выкачать из него 96 л воды. За одну минуту можно выкачать на 3 л
воды больше, чем накачать. Сколько литров воды накачивается в бак за минуту?
Решение.
Пусть за минуту в бак накачивается литров воды. Тогда за минуту выкачивается
воды.
По условию задачи составим уравнение:
л
,
откуда
Получаем квадратное уравнение
,
имеющее корни:
и
.
Отбрасывая отрицательный корень, находим, что за минуту в бак накачивается 9 л воды.
Ответ: 9.
23. C 3 № 311655. Постройте график функции
и определите, при каких
значениях построенный график не будет иметь общих точек с прямой
.
Решение.
Преобразуем функцию:
при
и
. График — прямая
без двух точек
и
. Прямая
не будет иметь с построенной
прямой общих точек, если она будет ей параллельна, т. е. при
, и если она будет про-
ходить через выколотые точки. Через первую из этих точек прямая
, а через вторую — если
проходит, если
.
Ответ:
24. C 4 № 76.
Найдите угол АСО, если его сторона СА касается
окружности, О — центр окружности, а дуга AD окружности, заключённая внутри этого
угла, равна 100°.
Решение.
Проведём радиус OA. Треугольник AOC — прямоугольный, ∠A =
90°. ∠COA = 180° − ∠AOD = 180° − 100° = 80°; ∠ACO = 90° − 80° = 10°.
О т в е т : 10.
25. C 5 № 311607. Дана равнобедренная трапеция
. Точка лежит на основании
и равноудалена от концов другого основания. Докажите, что — середина основания
.
Решение.
Треугольник
равнобедренный. Поэтому
В равнобедренной трапеции
.
.
Отсюда следует, что
. Значит, треугольники
сторонам и углу между ними. Следовательно,
.
и
равны по двум
26. C 6 № 311703. Длина катета
прямоугольного треугольника
равна 8 см. Окружность с диаметром
пересекает гипотенузу
в точке . Найдите площадь треугольника
, если известно, что
.
Решение.
потенуза
Пусть
см,
см. По теореме Пифагора:
см и
.
По теореме о секущей и касательной
.
Следовательно,
, откуда
.
Тогда
.
Следовательно, площадь треугольника равна
.
см. Поэтому ги-
Ответ:
.