*** *1
реклама
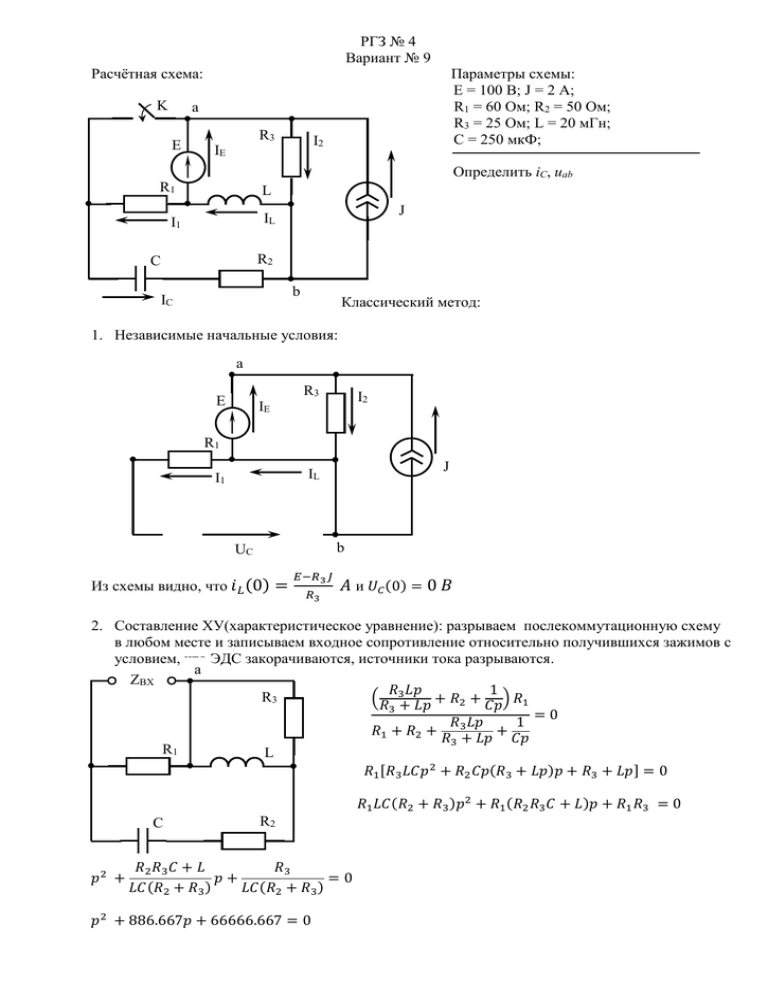
РГЗ № 4
Вариант № 9
Расчётная схема:
K
Параметры схемы:
E = 100 B; J = 2 A;
R1 = 60 Ом; R2 = 50 Ом;
R3 = 25 Ом; L = 20 мГн;
С = 250 мкФ;
a
E
R3
I2
IE
Определить iC, uab
R1
L
J
IL
I1
R2
C
b
IС
Классический метод:
1. Независимые начальные условия:
a
R3
E
I2
IE
R1
J
IL
I1
b
UС
Из схемы видно, что 𝑖𝐿 (0) =
𝐸−𝑅3 𝐽
𝑅3
𝐴 и 𝑈𝐶 (0) = 0 𝐵
2. Составление ХУ(характеристическое уравнение): разрываем послекоммутационную схему
в любом месте и записываем входное сопротивление относительно получившихся зажимов с
условием, что ЭДС закорачиваются, источники тока разрываются.
a
ZВХ
𝑅 𝐿𝑝
1
R3
(𝑅 3+ 𝐿𝑝 + 𝑅2 + 𝐶𝑝) 𝑅1
3
=0
𝑅 𝐿𝑝
1
𝑅1 + 𝑅2 + 3
+
𝑅3 + 𝐿𝑝 𝐶𝑝
R1
L
𝑅1 [𝑅3 𝐿𝐶𝑝2 + 𝑅2 𝐶𝑝(𝑅3 + 𝐿𝑝)𝑝 + 𝑅3 + 𝐿𝑝] = 0
𝑅1 𝐿𝐶(𝑅2 + 𝑅3 )𝑝2 + 𝑅1 (𝑅2 𝑅3 𝐶 + 𝐿)𝑝 + 𝑅1 𝑅3 = 0
C
𝑝2 +
R2
𝑅2 𝑅3 𝐶 + 𝐿
𝑅3
𝑝+
=0
𝐿𝐶(𝑅2 + 𝑅3 )
𝐿𝐶(𝑅2 + 𝑅3 )
𝑝2 + 886.667𝑝 + 66666.667 = 0
𝑝2 + 𝑏 ∙ 𝑝 + 𝑐 = 0
Решая квадратное уравнение, получим корни:
𝑝1,2 =
−𝑏±√𝑏 2 −4𝑐
2
𝑝1 = −82.948
𝑝2 = −803.719
3. Находим установившиеся значения при 𝑡 → ∞:
a
𝑖𝐶 (∞) = 0 𝐴
R3
E
I2
IE
𝑈𝑎𝑏 (∞) = 𝐸 = 100 В
R1
J
IL
I1
UС
b
4. Общий вид искомых величин:
𝑖𝐶 (𝑡) = 𝐴 ∙ 𝑒 𝑝1∙𝑡 + 𝐵 ∙ 𝑒 𝑝2∙𝑡 + 𝑖С (∞) = 𝐴 ∙ 𝑒 −82.948∙𝑡 + 𝐵 ∙ 𝑒 −803.719∙𝑡
𝑈𝑎𝑏 (𝑡) = 𝐴′ ∙ 𝑒 𝑝1∙𝑡 + 𝐵′ ∙ 𝑒 𝑝2∙𝑡 + 𝑈𝑎𝑏 (∞) = 𝐴′ ∙ 𝑒 −82.948∙𝑡 + 𝐵′ ∙ 𝑒 −803.719∙𝑡 + 100
5. Нахождение зависимых начальных условий с помощью независимых начальных условий:
составляем систему уравнений Кирхгофа в дифференциальной форме:
𝑑𝑖𝐿
𝑖𝐿 − 𝑖𝐸 − 𝑖1 = 0
𝑖𝐶 + 𝑖2 − 𝑖𝐿 = 𝐽
𝑅1 𝑖1 = −𝐸
𝑑𝑖𝐿
𝑅3 𝑖2 + 𝐿
=𝐸
𝑑𝑡
{𝐿 𝑑𝑡 + 𝑅1 𝑖1 +𝑈𝐶 + 𝑅2 𝑖𝐶 = 0
Вычитаем из 4-го уравнения 5-е:
𝑅3 𝑖2 − 𝑅1 𝑖1 −𝑈𝐶 − 𝑅2 𝑖𝐶 = 𝐸
(*)
Упростив это уравнение с учётом независимого начального условия на конденсаторе и 3-го
уравнения запишем:
𝑅3 𝑖2 = 𝑅2 𝑖𝐶
Выражаем из 2-го уравнения второй ток и подставляем в уравнение выше:
𝑖2 = 𝑖𝐿 + 𝐽 − 𝑖𝐶
𝑖𝐶 =
𝑅3 (𝐽 + 𝑖𝐿 (0))
𝑅2 + 𝑅3
Чтобы найти производную продифференцируем 3-е и (*), и с учётом этого, аналогичными
вычислениями, выражаем искомую производную:
𝑅1
𝑑𝑖1
𝑑𝑖
=0⟹ 1=0
𝑑𝑡
𝑑𝑡
𝑅3
𝑑𝑖2
𝑑𝑖
𝑖
𝑑𝑖
𝑑𝑖
𝑖
𝑑𝑖
− 𝑅1 1 − 𝐶 − 𝑅2 С = 0 ⟹ 𝑅3 2 − 𝐶 = 𝑅2 С
𝑑𝑡
𝑑𝑡 С
𝑑𝑡
𝑑𝑡 С
𝑑𝑡
Подставляем в последнее выражение:
𝑑𝑖2 𝑑𝑖𝐿 𝑑𝑖С
=
−
𝑑𝑡
𝑑𝑡
𝑑𝑡
Находим искомое значение:
𝑑𝑖𝐿 𝑖𝐶
𝑑𝑖𝐶 𝑅3 𝑑𝑡 − С
=
= 484.444 А/с
𝑑𝑡
𝑅2 + 𝑅3
Для напряжения:
𝑖2 = 𝑖𝐿 + 𝐽 − 𝑖𝐶 = 2.667 𝐴
𝑈𝑎𝑏 = 𝑅3 𝑖2 = 66.667 𝐵
Производная:
𝑑𝑈𝑐
𝑑𝑖𝐿 𝑑𝑖С
= 𝑅3 (
−
) = 29555.556 𝐵/𝑐
𝑑𝑡
𝑑𝑡 𝑑𝑡
6. Нахождение постоянных интегрирования:
для 𝑖𝐶 :
𝑖𝐶 (𝑡) = 𝐴 ∙ 𝑒𝑝1∙𝑡 + 𝐵 ∙ 𝑒𝑝2∙𝑡 + 𝑖1 (∞) = 𝐴 ∙ 𝑒−82.948∙𝑡 + 𝐵 ∙ 𝑒−803.719∙𝑡
{𝑑𝑖1
= 𝑝1 ∙ 𝐴 ∙ 𝑒𝑝1∙𝑡 + 𝑝2 ∙ 𝐵 ∙ 𝑒𝑝2∙𝑡 = −82.948 ∙ 𝐴 ∙ 𝑒−82.948∙𝑡 − 803.719 ∙ 𝐵 ∙ 𝑒−803.719∙𝑡
𝑑𝑡
подставляем найденные зависимые начальные условия в эту систему:
{
1.333 = 𝐴 + 𝐵
484.444 = 𝑝1 ∙ 𝐴 + 𝑝2 ∙ 𝐵 = −82.948 ∙ 𝐴 − 803.719 ∙ 𝐵
{
𝐵 = 1.333 − 𝐴
484.444 = 𝑝1 ∙ 𝐴 + 𝑝2 ∙ (1.333 − 𝐴) = −82.948 ∙ 𝐴 − 803.719 ∙ (1.333 − 𝐴)
(𝑝1 − 𝑝2 ) ∙ 𝐴 = 1556.07
{ ′
𝐵 = 1.333 − 𝐴
{𝐴 = 2.159
𝐵 = 1.333 − 𝐴 = −0.826
для 𝑈𝑎𝑏 :
𝑈𝑎𝑏 (𝑡) = 𝐴′ ∙ 𝑒𝑝1∙𝑡 + 𝐵′ ∙ 𝑒𝑝2∙𝑡 + 𝑈𝐶 (∞) = 𝐴′ ∙ 𝑒−82.948∙𝑡 + 𝐵′ ∙ 𝑒−803.719∙𝑡 + 100
{𝑑𝑈𝑎𝑏
= 𝑝1 ∙ 𝐴′ ∙ 𝑒𝑝1∙𝑡 + 𝑝2 ∙ 𝐵′ ∙ 𝑒𝑝2∙𝑡 = −82.948 ∙ 𝐴′ ∙ 𝑒−82.948∙𝑡 − 803.719 ∙ 𝐵′ ∙ 𝑒−803.719∙𝑡
𝑑𝑡
подставляем найденные зависимые начальные условия в эту систему:
{
66.667 = 𝐴′ + 𝐵′ + 100
29555.556 = 𝑝1 ∙ 𝐴′ + 𝑝2 ∙ 𝐵′ = −82.948 ∙ 𝐴′ − 803.719 ∙ 𝐵′
𝐵′ = −100 − 𝐴′
{
29555.556 = 𝑝1 ∙ 𝐴′ + 𝑝2 ∙ (−100 − 𝐴′ ) = −82.948 ∙ 𝐴′ − 803.719 ∙ (−100 − 𝐴′ )
′
{
(𝑝1 − 𝑝2 ) ∙ 𝐴 = 2764.925
𝐵′ = −100 − 𝐴′
′
{𝐴 = 3.836
𝐵′ = −37.169
Запишем окончательный вид искомых величин:
𝑖𝐶 (𝑡) = 𝐴 ∙ 𝑒 𝑝1∙𝑡 + 𝐵 ∙ 𝑒 𝑝2∙𝑡 + 𝑖С (∞) = 𝐴 ∙ 𝑒 −82.948∙𝑡 + 𝐵 ∙ 𝑒 −803.719∙𝑡 =
= 2.159 ∙ 𝑒 −82.948∙𝑡 − 0.826 ∙ 𝑒 −803.719∙𝑡
𝑈𝐶 (𝑡) = 𝐴′ ∙ 𝑒 𝑝1∙𝑡 + 𝐵′ ∙ 𝑒 𝑝2∙𝑡 + 𝑈𝑎𝑏 (∞) = 𝐴′ ∙ 𝑒 −82.948∙𝑡 + 𝐵′ ∙ 𝑒 −803.719∙𝑡 + 100 =
= 3.836 ∙ 𝑒 −82.948∙𝑡 − 37.169 ∙ 𝑒 −803.719∙𝑡 + 100
Операторный метод
K
a
R3
𝐸
𝑝
I2
IE
R1
LiL(0)
IС
𝐽
𝑝
IL
I1
1
𝑝𝐶
pL
R2
b
Составим систему уравнений по законам Кирхгофа в операторной форме:
𝐼𝐿 − 𝐼1 − 𝐼𝐸 = 0
𝐽
𝐼2 − 𝐼𝐿 + 𝐼𝐶 = 𝑝
𝐸
𝑅1 ∙ 𝐼1 = − 𝑝
𝐸
𝑅3 𝐼2 + 𝑝𝐿𝐼𝐿 = 𝑝 + 𝐿𝑖𝐿 (0)
1
{𝑅1 ∙ 𝐼1 + 𝑝𝐿𝐼𝐿 + (𝑅2 + 𝑝С) 𝐼𝐶 = 𝐿𝑖𝐿 (0)
Матричная форма:
0
𝐽
𝑝
𝐸
−
𝑝
0
𝐼1
−1 0 1
1 −1
𝐼2
0 1 −1 0
0
𝑅1 0 0
0 ∙ 𝐼𝐿 =
0
0 𝑅3 𝑝𝐿
𝐼𝐶
1 0
𝐸
𝑅1 0 𝑝𝐿 𝑅2 +
0 [ ]
+ 𝐿𝑖𝐿 (0)
[
𝑝С ] 𝐼𝐸
𝑝
[ 𝐿𝑖𝐿 (0) ]
Решаем через обратную матрицу:
0 −1
𝐼1
−1 0 1
𝐼2
0 1 −1 1
0
0
𝐼𝐿 = 𝑅1 0 0
0
0 𝑅3 𝑝𝐿 0 1 0
𝐼𝐶
[𝐼𝐸 ] [ 𝑅1 0 𝑝𝐿 𝑅2 + 𝑝С 0 ]
0
−1
𝐽
𝑝
𝐸
−𝑝
∙
𝐸
𝑝
+ 𝐿𝑖𝐿 (0)
[ 𝐿𝑖𝐿 (0) ]
Запишем отдельно:
𝐼1 =
−1,667
𝑝
2
𝐼2 =
2.667 p 3546.667 p 266666.667
p2 886.667p 66666.667p
2
𝐼𝐿 =
𝐼𝐶 =
2 p 3440 p 133333.333
p2 886.667p 66666.667p
1.333 p 1666.667
2
p 886.667 p 66666.667
2
𝐼𝐸 =
3.667 p 4917.778 p 244444.444
p2 886.667 p 66666.667 p
Находим искомые величины:
𝐼𝐶 (𝑝) = 𝐼𝐶 =
1.333 p 1666.667
2
p 886.667 p 66666.667
2
𝑈𝑎𝑏 (𝑝) = 𝑅3 𝐼2 = 𝑅3 (
2
2.667 p 3546.667 p 266666.667
p2 886.667p 66666.667p
)=
66.667 p 88666.667 p 6666666.667
p2 886.667p 66666.667p
Возьмём обратное преобразование Лапласа от изображения 𝐼𝐶 (𝑝) и наёдем его оригинал:
Чтобы найти оригинал, воспользуемся теоремой разложения, наше изображение имеет вид:
,где
.
Оригинал будет рассчитываться по формуле:
, где
Если один из корней
- к-й корень уравнения
.
равен нулю, то формула приводится к такому виду:
,где
.
Корни знаменателя:
𝑝1 = −82.948
𝑝2 = −803.719
1.333 p 1666.667
𝑖𝐶 (𝑡) =
1
1.333 p 1666.667
∙𝑒
2 p 886.667
−82.948𝑡
+
1
=
1.333 ( 82.948) 1666.667
2 ( 82.948) 886.667
∙ 𝑒 −82.948𝑡 +
2
2 p
2
886.667
1.333 ( 803.719) 1666.667
2 ( 803.719) 886.667
∙ 𝑒 −803.719𝑡 =
∙ 𝑒 −803.719𝑡 =
= 2.159 ∙ 𝑒 −82.948𝑡 − 0.826 ∙ 𝑒 −803.719𝑡
Для 𝑈𝑎𝑏 (𝑡):
12 88666.667p1 6666666.667 𝑝 𝑡 66.667p22 88666.667p2 6666666.667 𝑝 𝑡
∙𝑒 +
∙𝑒 +
2 p1 886.667 p1
2p2 886.667p2
66.667 p
𝑈𝑎𝑏 (𝑡) =
1
2
2
+𝑈𝑎𝑏 (∞) =
66.667 ( 82.948) 88666.667 82.948 6666666.667
( 2 82.948 886.667) 82.948
∙ 𝑒 −82.948𝑡 +
2
+
66.667 ( 803.719) 88666.667 803.719 6666666.667
( 2 803.719 886.667) 803.719
= 3.836 ∙ 𝑒 −82.948𝑡 − 37.169 ∙ 𝑒 −803.719𝑡 + 100
Строим графики:
∙ 𝑒 −803.719𝑡 + 100 =
i( t) 2.159 e
82.948 t
0.826 e
803.719 t
1.7
1.5
1.3
1.1
0.9
i( t )
0.7
0.5
0.3
0.1
0.1
0
0.02
0.04
0.06
0.08
0.045
0.06
t
Uab( t) 3.836 e
82.948 t
37.169 e
803.719 t
100
105
101.54
98.08
94.62
91.15
87.69
84.23
Uab( t )
80.77
77.31
73.85
70.38
66.92
63.46
60
0
0.015
0.03
t



