task_15986x
реклама

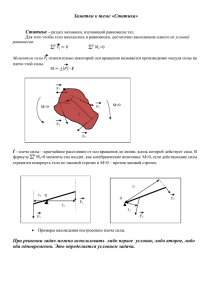
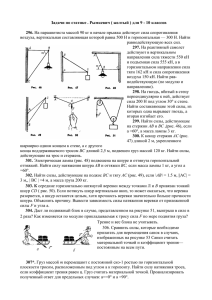
Задача №1 Сигнальная ракета, выпущенная на большой высоте под углом β0 к горизонту со скоростью v0, через время t разрывается на две части массами m1 и m2, продолжающими двигаться в плоскости траектории ракеты. В начальный момент времени после разрыва вектор скорости v1 первого осколка составляет с горизонтальной осью угол α1, а вектор скорости v2 второго осколка – соответственно угол α2 (положительные углы соответствуют направлению отсчета от горизонтальной оси против часовой стрелки) Определить для 1-го осколка через 8с после разрыва ракеты 1. модуль приращения импульса |∆p1|; 2. приращение модуля импульса ∆|p1|; 3. нормальное an и тангенциальное aт ускорение осколка; 4. радиус кривизны траектории движения осколка; β0 = 35 градусов v0 = 70 м/c m1 = 0,06 кг m2 = 0,04 кг α1 = 0 градусов α2 = 60 градусов t=2c Задача №2 Тонкий стержень длиной l0 и массой m0 может свободно вращаться вокруг горизонтальной оси, проходящей на расстоянии l от его верхнего конца. Шар массой m и радиусом R закреплен на оси стержня на расстоянии l2 от нижнего конца стержня. Пуля массой m1 летящая горизонтально со скоростью v1 попадает в стержень на расстоянии l1 ниже точки подвеса и пробивает его. Скорость пули на вылете из стержня равна v2. В момент попадания пули стержень находился в вертикальном положении и двигался с угловой скоростью ɷ1 (положительное значение ɷ1 соответствует движению стержня в одном направлении с пулей, отрицательное в противоположном). В первый момент времени после удара угловая скорость стержня ɷ1. Определить: 1. максимальный угол, на который отклонился стержень; 1 2. количество выделившегося при ударе тепла; 3. изменение кинетической энергии стержня в начальный момент времени после удара пули. m =1,0 кг m0 = 1,5 кг m1 = 0,02 кг R = 0,3 м l = 0,4 м l0 = 1,4 м l1 = 0,4 м l2 = 0,4 м v1 = 740 м/c v2 = 546 м/c ɷ1 = 0,5 с1 ɷ2 необходимо найти Задача №3 Два шара массами m1 и m2 и радиусами R1 и R2 насажены на тонкие стержни, имеющие длины l1 и l2 и массы m3 и m4 так, что центры шаров находятся на одинаковом расстоянии l0 от точек подвеса стержней. Расстояние между точками подвеса стержней равно R1 + R2. Шары, движущиеся с угловыми скоростями ɷ1 и ɷ2 относительно точек подвеса стержней, сталкиваются в тот момент, когда стержни находятся в вертикальном положении. После столкновения шаров их угловые скорости стали равными ɷʹ1 и ɷʹ2. Определить: 1. количество выделившегося в результате удара тепла 2. максимальный угол, на который отклонится 2-ой стржень. m1 = 0,6 кг m2 = 1,6 кг R1 = 0,3 м R2 = 0,3 м m3 = 0,5 кг m4 = 1,0 кг l1 = 1,5 м l2 = 1,5 м l0 = 0,6м 2 ɷ1 = 0,5 с1 ɷ2 = 1,5 с1 ɷʹ1 = 1,9 с1 ɷʹ2 необходимо найти Задача №4 Тело массой m под действием квазиупругой силы совершает гармонические колебания в двух взаимно перпендикулярных направлениях по законам x=a·sin (cot+α1) y= b·cos(cot+ α2) Определить для моментов времени t 1. скорость и ускорение тела; 2. величину квазиупругой силы; 3. кинетическую и потенциальную энергию ɷ = N рад/c t=Nc a = N см b = 30-N см α1 = π/N рад α2 = π/N рад m = 30-N грамм N = 23 Задача №5 В начальный момент времени диск массой m, находящийся на высоте h0 от основания наклонной плоскости, составляющей угол α с горизонтом, катится вверх со скоростью v0. Через промежуток времени ∆t скорость центра масс диска стала равной v, а диск прошел путь s, оказавшись на расстоянии l от основания наклонной плоскости. В этот момент времени кинетическая энергия диска равна Wк. Определить: m, h0, α (градусы), s. v0 = 20 м/с ∆t = 4 с v = 12 м/c l = 70 м Wк = 200 Дж 3