7 Колебания

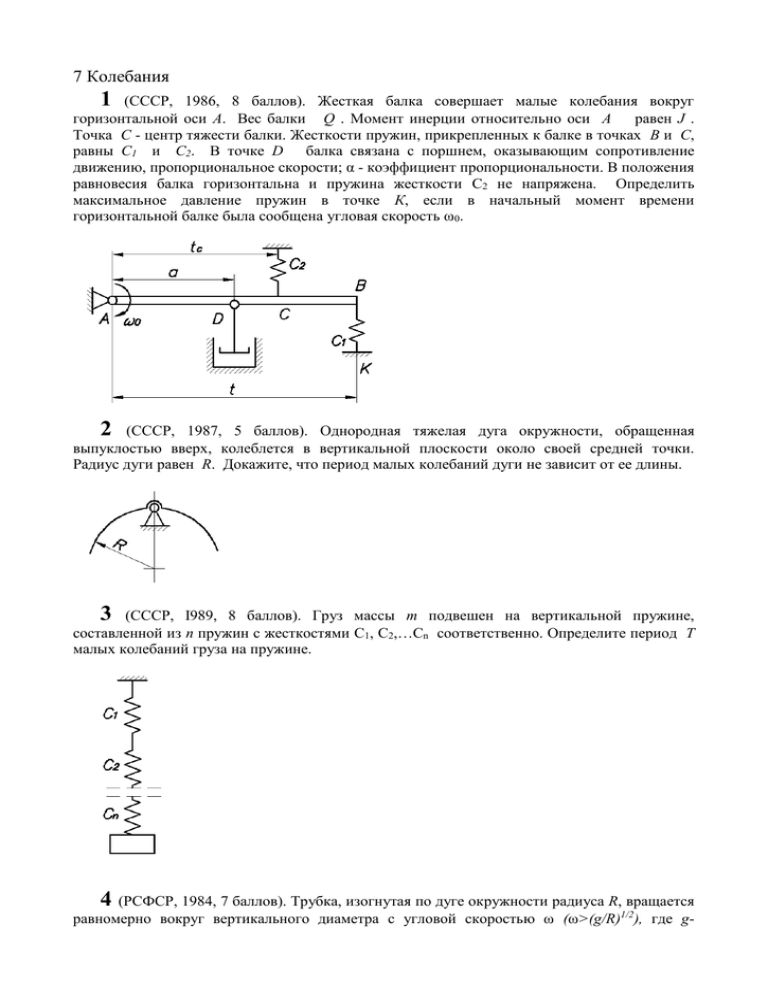
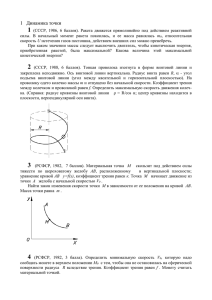
7 Колебания
1
(СССР, 1986, 8 баллов). Жесткая балка совершает малые колебания вокруг
горизонтальной оси А. Вес балки Q . Момент инерции относительно оси А
равен J .
Точка С - центр тяжести балки. Жесткости пружин, прикрепленных к балке в точках В и С,
равны C1 и С2. В точке D балка связана с поршнем, оказывающим сопротивление
движению, пропорциональное скорости; α - коэффициент пропорциональности. В положения
равновесия балка горизонтальна и пружина жесткости C2 не напряжена. Определить
максимальное давление пружин в точке К, если в начальный момент времени
горизонтальной балке была сообщена угловая скорость ω0.
2 (СССР, 1987, 5 баллов). Однородная тяжелая дуга окружности, обращенная
выпуклостью вверх, колеблется в вертикальной плоскости около своей средней точки.
Радиус дуги равен R. Докажите, что период малых колебаний дуги не зависит от ее длины.
3
(СССР, I989, 8 баллов). Груз массы m подвешен на вертикальной пружине,
составленной из n пружин с жесткостями C1, C2,…Сn соответственно. Определите период Т
малых колебаний груза на пружине.
4 (PCФCP, 1984, 7 баллов). Трубка, изогнутая по дуге окружности радиуса R, вращается
равномерно вокруг вертикального диаметра с угловой скоростью ω (ω>(g/R)1/2), где g-
ускорение свободного падения. Внутри трубки может двигаться без трения шарик М.
Определить закон малых колебаний шарика около положения относительного равновесия.
Шарик считать материальной точкой.
5
(РСФСР, 1985, 5 баллов). Тяжелый грузик 1 прикреплён к телу 2 при помощи
идеального шарового шарнира и невесомого стержня длиной l. Движение происходит на
горизонтальной негладкой плоскости (коэффициент трения скольжения между грузиком и
плоскостью равен f ) Стержень не касается плоскости, а тело имеет постоянную скорость U.
Определить период малых колебании грузика. При каких значениях
U
возможны
периодические колебания?
6 (РСФСР, 1988, 7 баллов). Однородный сплошной диск 1 весом G1 охвачен гибкой
лентой; один ее конец соединен с пружиной, имеющей жесткость с, а ко второму прикреплен
груз 2 весом G2. Лента по диску не проскальзывает. Грузу сообщена скорость V0 из
положения покоя. Определить период колебании и закон движения груза. Массы пружины и
ленты не учитывать.
7 (PCФCP, 1986, 7 баллов). Цилиндр со смещенным с оси центром тяжести опирается на
негладкую цилиндрическую поверхность такого же, как у цилиндра, радиуса r. Коэффициент
сцепления (трения покоя) равен f.
Определять область устойчивости цилиндра (максимальный угол поворота) и смещение
ρ его центра тяжести, при котором цилиндр, отклоненный от положения равновесия,
показанного на рисунке, будет к нему возвращаться. Трение качения не учитывать.