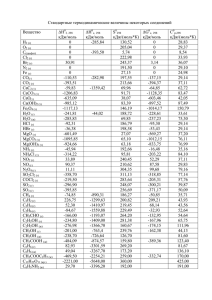
Контрольная работа №1 Тема: Химическая термодинамика Задача 1. Определить плотность синтез-газа при 410 ◦С и давлении 2 МПа. Состав газа приведен в таблице 1. Таблица 1 – Содержание компонентов синтез-газа (%об.) Вариант 4 СО 25 Н2 65 СО2 8 СН4 1 𝑁2 1,0 Решение: Плотность определяем по формуле 𝜌= 𝑃, 𝑀𝑟см 𝑅𝑇 Находим молярные массы веществ: M(CO) = 28×10-3 кг/моль; М(H2) = 2×10-3 кг/моль; М(CO2) = 44×10-3 кг/моль; М(СH4) = 16×10-3 кг/моль; М(N2) = 28×10-3 кг/моль. По правилу смешения находим среднюю молярную массу газовой смеси: 𝑀𝑟см = 𝑥 (𝐶𝑂), 𝑀𝑟 (𝐶𝑂) + 𝑥 (𝐻2 ), 𝑀𝑟(𝐻2) + 𝑥 (𝐶𝑂2 ), 𝑀𝑟(𝐶𝑂2 ) + 𝑐 (𝐶𝐻4 ) ∗ 𝑀𝑟 (𝐶𝐻4 ) + 𝑥 (𝑁2 ) ∗ 𝑀𝑟 (𝑁2 ) 𝑀𝑟см = 0,25 ∗ 28 + 0,65 ∗ 2 + 0,08 ∗ 44 + 0,01 ∗ 16 + 0,01 ∗ 28 = 12,26 г/моль Далее вычислим плотность синтез-газа, подставив известные значения: 2 ∗ 106 ∗ 12,26 г 𝜌= = 4318 3 = 4,318 кг/м3 8,314 ∗ 683 м Вишняков А.В., Кизим Н.Ф. Физическая химия. Учебник для ВУЗ-ов.М.: Химия, 2012, -840с., С.92) Задача 2 Определить концентрацию и плотность газа при температуре Т и давлении Р. Значения Т и Р приведены в таблице 2. Таблица 2 - Давление и температура газа Вариант 2 Газ Аммиак Температура, °C 250 Давление, МПа 30 Решение: Постоянные: Для определения концентрации молекул взятого газа применим равенство: 𝑃 = 𝑛𝑘𝑇 k - постоянная Больцмана (k = 1,38 * 10-23 Дж/К). P (давление газа) откуда 𝑃 30 ∗ 106 𝑛= = = 4,2 ∗ 1027 м−3 𝑘𝑇 1,38 ∗ 10−23 ∗ 523 Плотность газа при температуре Т (К) и давлении Р: , где . Здесь Т0 = 273 К, р0 = 760 мм рт.ст = 1,013 * 105 Па = 0,1013 МПа Vm = 22,4 м3/кмоль. 𝜌0 = 17 = 0,76 кг/м3 22,4 𝜌(𝑁𝐻3) = 0,76 ∗ 273 30 ∗ = 117 кг/м3 523 0,1013 pV = (m/μ) * RT. Плотность: ρ = m/V. Перепишем так: pμ = (m/V)*RT pμ = ρ*RT ρ = pμ/(RT) = 0,30 * 106 * 32 * 10-3/(8,31 * 250) = 3,851 кг/м3. Ответ: ρ = 3,851 кг/м3. Вишняков А.В., Кизим Н.Ф. Физическая химия. Учебник для ВУЗ-ов.М.: Химия, 2012, -840с.(с. 392) Задача 3 Воздух с исходной температурой Т и давлением 1 атм сжимается адиабатически или изотермически до давления Р. Определить расход энергии на сжатие и теплоотвод от компрессора при ведении процесса. Воздух считать двухатомным идеальным газом. Значения Т и Р приведены в таблице 3. Таблица 3- Исходная температура и конечное давление Вариант Температура, °C 4 12 Давление, МПа 3,5 Решение: При изотермическом сжатии A = Q = nRT ln(p2/p1) При адиабатическом, Q = 0 (теплоотвод). Дальше нужно найти n, количество молекул можно найти из формулы p = nkT 𝑃 3,5 ∗ 106 𝑛= = = 8,9 ∗ 1026 м−3 −23 𝑘𝑇 1,38 ∗ 10 ∗ 285 При изотермическом сжатии 26 𝑄 = 8,9 ∗ 10 3,5 ∙ 106 ∗ 8,314 ∗ 285 ∗ ln ( ) = 7,47 ∗ 1030 Дж 101300 Из соотношения параметров в адиабатном процессе имеем К где = 1,4 – показатель адиабаты воздуха. Затраченная работа Конечный объем кДж/кг. м3/кг. Вишняков А.В., Кизим Н.Ф. Физическая химия. Учебник для ВУЗ-ов.М.: Химия, 2012, -840с., (С.185) Задача 4. Вариант 6 Рассчитать теплоту перехода ромбической серы в моноклинную, если теплоты сгорания при температуре перехода, равны (-297,5) кДж/моль (ромбическая) и (-300,1) кДж/моль. Решение: Следствие закона Гесса: Qпер(Sромб - Sмон) = Qсг(Sромб) - Qсг(Sмон) Qпер(Sромб - Sмон) =-297,5-(-300,1)=2,6 кДж Вишняков А.В., Кизим Н.Ф. Физическая химия. Учебник для ВУЗ-ов.М.: Химия, 2012, -840с., (С.159) Задача 5 Определить тепловой эффект реакции, проводимой при стандартном давлении и температуре Т. Показать графически зависимость теплового эффекта реакции и изменения изобарной теплоемкости от температуры. Интервал изменения температур выбрать самостоятельно так, чтобы отразить особенности поведения этих функций, если они имеются. Уравнение реакции и температура приведены в таблице 5. Таблица 5. Уравнение реакции и значение температуры. Вариант Уравнение реакции Т,°С 10 2С6Н6(г) + 2НСl(г) + О2(г) = 2С6Н5Сl(г) + 2Н2О(г) 250 Решение: Для расчета теплового эффекта используем справочные данные. Таблица - Справочные данные по стандартным теплотам образования, энтропии для веществ, участвующих в реакции Вещество 0 ∆𝐻298 , кДж /моль Cp, a b*103 c*106 c*10-5 Дж/моль*К С6Н6(г) 82,93 81,67 -33,9 471,87 -298,3 НСl(г) -92,3 29,16 26,53 4,6 - 1,09 О2(г) 0 29,36 31,46 3,39 - -3,77 С6Н5Сl(г) -618,6 188,4 - - - - Н2О(г) -241,84 33,56 30 10,71 - 0,33 2С6Н6(г) + 2НСl(г) + О2(г) = 2С6Н5Сl(г) + 2Н2О(г) Рассчитаем тепловой эффект реакции при Т=298 К ( закону Гесса: 0 0 ∆𝐻𝑟0 = ∑ 𝜈𝑖 ∆𝐻𝑖(прод) − ∑ 𝜈𝑖 ∆𝐻𝑖(исх) где, прод – продукты реакции; исх – исходные вещества; i– стехиометрические коэффициенты в уравнении реакции. по 0 ∆𝐻298 = (2∆𝐻0 (𝐻2 𝑂) + 2∆𝐻0 (𝐶6 𝐻5 𝐶𝑙 )) − (∆𝐻0 (О2 ) + 2∆𝐻0 (𝐻𝐶𝑙 ) + 2∆𝐻0 (𝐶6 𝐻6 )) = (2 ∙ −241.84 + 2 · (−618.6) − (0 + 2 ∗ −92.3 + 2 ∙ 82.93) = −1702,14 кДж Определим изменение средней теплоемкости для нашей реакции в интервале температур 298÷900 К. Для этого используем данные, внесенные в табл. 0 0 ∆𝐶𝑝0 = ∑ 𝜈𝑖 ∆𝐶𝑝(прод) − ∑ 𝜈𝑖 ∆𝐶𝑝(исх) 0 ∆𝐶𝑝.298 = (2∆𝐶𝑝0 (𝐻2 𝑂) + 2∆𝐶𝑝0 (𝐶6 𝐻5 𝐶𝑙 )) − (∆𝐶𝑝0 (О2 ) + 2∆𝐶𝑝0 (𝐻𝐶𝑙 ) + 2∆𝐶𝑝0 (𝐶6 𝐻6 )) = (2 ∙ 33.56 + 2 · (188.4) − (29.36 + 2 ∗ 29.16 + 2 ∙ 81.67) = 192.9 Дж/К Определим тепловой эффект при заданной температуре Т =523 К для нашей реакции. Тепловой эффект при заданной температуре находится по интегральной форме уравнения Кирхгофа: 0 0 0 (Т − 298) = −1702140 + 192,9(523 − 298) = −1658737 Дж ∆𝐻523 = ∆𝐻298 + ∆𝐶𝑝.298 Покажем графически зависимость теплового эффекта реакции и изменения изобарной теплоемкости от температуры. Т= 298; 523; 650; 1000; 1500. Рассчитаем тепловой эффект реакции при разных температурах 0 ∆𝐻650 = −1702140 + 192,9(650 − 298) = −1634239 Дж 0 ∆𝐻1000 = −1702140 + 192,9(1000 − 298) = −1566724 Дж 0 ∆𝐻1500 = −1702140 + 192,9(1500 − 298) = −1470274 Дж При точных расчетах необходимо учитывать температурную зависимость ΔСP = f(T). Так как для каждого вещества, участвующего в химической реакции, установлено уравнение, описывающее зависимость его теплоемкости от температуры, то в этом случае разность теплоемкостей ΔСPбудет представлять собой уравнение, которое в общем виде записывается следующим образом: ΔСP = Δa + Δb·T + Δc ·T2 + Δc΄/ T2 где Δa, Δb, Δc, Δc΄– изменения коэффициентов соответствующих степенях, полученные при расчете ΔСP. при Тв Рассчитаем изменение теплоемкости реакции при стандартных условиях. Для этого найдем коэффициенты Δа, Δb, Δc для данной реакции: Δа =(2∙30) – (31.46+2∙26.53+2∙-33.9) = 43.28 Δb = -934.91∙10-3 Δc’ = 2.25*10-5 Δc=298.3*10-6 ∆С1000 = 43,28 − 934,91 ∙ 10−3 ∙ 1000 + р 2,25 ∙ 105 298,3 ∙ 106 − 10002 10003 = −891,7 Дж/К ∆С523 = 43,28 − 934,91 ∙ 10−3 ∙ 523 + р 2,25 ∙ 105 298,3 ∙ 106 − 5232 5233 = −446,9 Дж/К ∆С1500 = 43,28 − 934,91 ∙ 10−3 ∙ 1500 + р 2,25 ∙ 105 298,3 ∙ 106 − 15002 15003 = −1359 Дж/К Построим график зависимости теплового эффекта от температуры -1450 0 200 400 600 800 1000 1200 1400 1600 -1500 ∆Н, кДж -1550 -1600 -1650 -1700 -1750 Т, К Построим график зависимости теплоемкости от температуры 400 200 0 Ср, Дж/К -200 0 200 400 600 800 1000 1200 1400 1600 -400 -600 -800 -1000 -1200 -1400 -1600 Т, К Вишняков А.В., Кизим Н.Ф. Физическая химия. Учебник для ВУЗ-ов.М.: Химия, 2012, -840с., С.286) Задача 6 Газообразные хлор и водород при 25 °C поступают в реактор, где при 700 °C взаимодействуют по реакции Сl2 + Н2 = 2НСl(г) Определить изменение энтропии системы, с момента поступления газов в реактор, если их объемный расход одинаков. Решение: Процесс состоит из трех стадий: смешение исходных веществ, нагревание их до температуры 700 °С и химическое превращение. В соответствии с этим изменение энтропии системы включает в себя следующие энтропии: смешения Sсмеш; изобарического нагревания компонентов SрH2 и SрCl2; химического превращения ∆Sх.р. Проведем расчет на один пробег реакции. Исходная смесь состоит из 1 моль H2(г) и 1 моль Cl2(г), следовательно, молярные доли компонентов перед началом реакции одинаковы: x1= x2 = 0,50. Отсюда имеем S = −8,314(1∙ln 0,5 +1∙ln 0,5) =11,53 Дж/(К·пробег). Определяем изменение энтропии при изобарном нагревании компонентов системы по отдельности: для H2(г) SрH2 = 29,57 ∙ ln 973/298 = 35,0 Дж/(К·пробег); для Cl2(г) SрCl2 = 36,50∙ ln 973/298 = 43,2 Дж/(К·пробег); где 29,57 и 36,50 – значения изобарных теплоемкостей водорода и хлора, Дж/(моль·К), средние в температурном интервале 25–700 °С (298–973 К). Изменение энтропии системы на стадии химического превращения определяем по закону Гесса, значения стандартных энтропий участников реакции берем из приложения: для водорода S0298 = 130,52 Дж/(моль·К); для хлора S0298 = 222,98 Дж/(моль·К); для хлороводорода S0298 = 186,79 Дж/(моль·К). Исходя из следствия из закона Гесса, имеем Sх.р = 2·186,79 – (130,52 + 222,98) = 20,08 Дж/К. Суммируя результаты расчетов для всех стадий процесса, получаем ∆S=∆Sсм+∆SрH2 + ∆SрCl2 + S0p = 11,53+35+43,2+20,08=109,81 Дж/К Вишняков А.В., Кизим Н.Ф. Физическая химия. Учебник для ВУЗ-ов.М.: Химия, 2012, -840с., С.40) Задача 7 Вариант 2 При комнатных температурах серная кислота термически устойчива, а при повышенной - диссоциирует по реакции H2SO4(ж) ->SO3(г) + Н2О(г) Рассчитать температуру, при которой эта реакция термодинамически возможна. Решение: Самопроизвольное протекание реакции показывает величина энергии Гиббса, которая рассчитывается по формуле: ∆𝐺𝑟0 = ∆𝐻𝑟0 − 𝑇∆𝑆𝑟0 0 Рассчитаем энтальпию химической реакции H r (тепловой эффект химической реакции), используя следствие из закона Гесса. 0 0 ∆𝐻𝑟0 = ∑ 𝜈𝑖 ∆𝐻𝑖(прод) − ∑ 𝜈𝑖 ∆𝐻𝑖(исх) где, прод – продукты реакции; исх – исходные вещества; i– стехиометрические коэффициенты в уравнении реакции. Рассчитаем энтропию химической реакции, используя значения S 0(298) для всех веществ, участвующих в реакции. Значения S0r можно рассчитать по уравнению: 0 0 ∆𝑆𝑟0 = ∑ 𝜈𝑖 𝑆𝑖(прод) − ∑ 𝜈𝑖 𝑆𝑖(исх) Таблица 1 - Термодинамические свойства веществ 0 ∆𝐻298 , кДж/моль 0 𝑆298 , Дж/моль*К H2SO4(ж) -811,3 156,9 SO3(г) -395,2 256,23 Н2О(г) -241,84 188,74 H 0f (298) и G 0f (298) – стандартные энтальпия образования и энергия Гиббса образования веществ; S0 (298) – стандартная энтропия вещества. ∆𝐻𝑟0 = (∆𝐻 0 (𝑆𝑂3 ) + ∆𝐻 0 (Н2 𝑂)) − (∆𝐻 0(𝐻2 𝑆𝑂4 ) = = (−395.2 − 241.84) − (−811.3) = 174,26 кДж ∆𝑆𝑟0 = (𝑆 0 (𝑆𝑂3 ) + 𝑆 0(𝐻2𝑂)) − (𝑆 0 (𝐻2𝑆𝑂4 )) = (256,23 + 188.72) − (156.9) = 288,05 Дж/К Следовательно: ∆𝐺𝑟0 = ∆𝐻𝑟0 − 𝑇∆𝑆𝑟0 Рассчитаем энергию Гиббса при 298 К 0 ∆𝐺298 = 174260 − 298 ∙ 288,05 = 88421 Дж Так как G r > 0, процесс термодинамически не возможен. 0 Рассчитаем равновесную температуру Т р, для этого выразим величины H 0r и S0r в одинаковых единицах (кДж): Тр = H 0r / S0r Тр = 174260 = 605 К 288,05 При данной температуре и выше реакция термодинамически возможна. 0 ∆𝐺298 = 174260 − 605 ∙ 288,05 = −10,25 Дж Вишняков А.В., Кизим Н.Ф. Физическая химия. Учебник для ВУЗ-ов.М.: Химия, 2012, -840с., С.96) Тема: Фазовые равновесия Задача 1 Вариант 2 Воспользовавшись условиями задачи 1 и данными Приложения П1: 1. построить графики зависимостей Р - Т, К и InP- 1/Т, К-1 ; 2. вывести эмпирическое уравнение прямой InP= А + В/Т для процесса возгонки (определить коэффициенты А и В); 3. вычислить теплоту возгонки по эмпирическому уравнению прямой; 4. рассчитать теплоту испарения для двух, выбранных Вами, интервалов температур по уравнению Клапейрона-Клаузиуса; 5. определить теплоту плавления вещества в тройной точке; 6. вычислить температуру плавления вещества при нескольких значениях давления Р, Па; вычислить ∆S, ∆А, ∆G, ∆Uдля процесса испарения 1 кмоль 7. вещества в тройной точке. Решение: Вариант 3 Твердое состояние Жидкое состояние Условия Р∙10-5, Па Т,К Р, Па Т,К Р, Па 183,2 333,3 201,2 4669,5 М=64 50 186,2 1466 214,2 7169 dтв=1600 500 199,2 2799 219,2 7998 dж=1560 203,7 5305 230,2 13328 244 21728 Решение: 1. Построим графики зависимостей Р - Т,К для твердого состояния 6000 5000 y = 203.73x - 36860 Р, Па 4000 3000 2000 1000 0 180 185 190 195 Т, К для жидкого состояния 200 205 25000 P, Па 20000 15000 10000 5000 0 0 50 100 150 200 250 300 150 200 250 300 Т, К Общий 25000 20000 Р, Па 15000 10000 5000 0 0 50 100 -5000 Т, К InP- 1/Т, К-1 Твердое состояние Жидкое состояние 1/Т,К∙103 lnР, Па 1/Т,К lnР, Па 5.46 5.81 4.97 8.45 5.37 7.3 4.7 8.9 5.02 7.9 4.6 9.0 4.91 8.6 4.3 9.5 4.1 10.0 для твердого 10 9 8 7 y = -4.0842x + 28.599 lnP 6 5 4 3 2 1 0 4.8 4.9 5 5.1 5.2 5.3 5.4 5.5 5 6 1/Т∙1000 для жидкого 10.2 10 9.8 9.6 lnP 9.4 9.2 9 8.8 8.6 y = -1.7359x + 17.041 8.4 8.2 0 1 2 3 4 1/T∙1000 12 10 lnP 8 y = -2.6024x + 20.942 6 4 2 0 0 1 2 3 1/Т∙1000, К-1 4 5 6 2. Выведем эмпирическое уравнение прямой InP= А + В/Т для процесса возгонки (определим коэффициенты А и В). Проводим неопределенное интегрирование уравнения и получаем уравнение прямой, не проходящей через начало координат: 𝑙𝑛𝑃 = − ∆𝐻 1 ∙ + 𝑐𝑜𝑛𝑠𝑡 𝑅 𝑇 По тангенсу угла наклона прямой определяем среднюю энтальпию испарения или возгонки: Для испарения: tgα = − ∆Hф. п 𝑅 ∆Hф. п = −𝑅 ∙ 𝑡𝑔𝛼 = −2.303 ∙ 8.314 ∙ 𝑡𝑔𝛼 tgα = 8.6 − 7.9 = 6364 (5.02 − 4.91) ∙ 10−3 ∆Hф. п = −𝑅 ∙ 𝑡𝑔𝛼 = −2.303 ∙ 8.314 ∙ 6364 = −121852 Дж А=20,94 В=− ∆𝐻 1 121852 𝑅 8,314∙298 ∙ = 𝑇 = 49 3. вычислить теплоту возгонки по эмпирическому уравнению прямой. Для жидкого состояния вычислим тангенс tgα = 8.9 − 8.45 = 1667 (4.97 − 4.7) ∙ 10−3 ∆Hвозг = −𝑅 ∙ 𝑡𝑔𝛼 = −8.314 ∙ −4084 = 33954 Дж 𝑙𝑛𝑃ж = − 4084 + 28,59 Т 4. рассчитать теплоту испарения для двух, выбранных Вами, интервалов температур по уравнению Клапейрона-Клаузиуса. Для испарения: 𝑙𝑛𝑃ж = − 1735 + 17,04 Т ∆Hисп = −𝑅 ∙ 𝑡𝑔𝛼 = −8.314 ∙ −1735 = 14425 Дж 5. определим теплоту плавления вещества в тройной точке; Теплоту плавления вещества в тройной точке найдем по закону Гесса: ∆Нпл = ∆Нвозг – ∆Нисп = 33954−14425 = 19529 Дж/моль. 6. вычислим температуру плавления вещества при нескольких значениях давления Р, Па. Температуру плавления вещества при давлении Р=500∙10-5Па вычислим по формуле: 𝑇=𝑇тр.т+𝑑𝑇/𝑑𝑃(𝑃−𝑃тр.т)=199,2+3,5-9∙(500∙10-5−50∙10-5)=199,35 25000 20000 Р, Па 15000 10000 5000 0 0 -5000 50 100 150 200 250 300 Т, К 7. вычислить ∆S, ∆А, ∆G, ∆Uдля процесса испарения 1 кмоль вещества в тройной точке. Изменение энтальпии возгонки нами было вычислено ранее: Δ𝐻возг=33954 Дж/моль. Изменение внутренней энергии: Δ𝑈возг=Δ𝐻возг−𝑅·𝑇тр.т=33954−8,31·199,2=32298,7Джмоль. Изменение энтропии при этом: Δ𝑆возг=Δ𝐻возг𝑇тр.т=6763636=676Джмоль∙𝐾 . Изменение энергии Гиббса в фазовом переходе: Δ𝐺возг=0 Дж/моль. Изменение энергии Гельмгольца: Δ𝐴возг=Δ𝐺возг−𝑅·𝑇тр.т=−8,31·199,2=−1655,3 Дж/моль. ∆𝑆 = ∆𝐻 33954 = = 170 Дж/К 𝑇 200 (Вишняков А.В., Кизим Н.Ф. Физическая химия. Учебник для ВУЗ-ов.-М.: Химия, 2012, -840с., С.205) Разбавленные растворы Вариант 10. Раствор, содержащий 1 г КСl в 100 г воды замерзает при 271,54 К. Определить изотонический коэффициент Вант - Гоффа, степень диссоциации и давление пара этого раствора при 298 К, если давление пара воды при этой температуре равно 3166,67 Па. Криоскопическая константа воды 1,86 К. Степень диссоциации КСl считать не зависящей от температуры. Решение: Определим понижение температуры кристаллизации t(крист) раствора без учёта диссоциации KCl (криоскопическая константа для воды равна 1,86) по формуле: ∆𝑡 = 𝐾 ∙ 𝑚1 ∙ 1000 1,86 ∙ 1 ∙ 1000 = = 0.25 °𝐶 𝑚2 ∙ 𝑀 100 ∙ 74.5 где m1 - масса растворённого вещества, m2 - масса раствора, М – молярная масса растворённого вещества, К – криоскопическая константа. Сравнивая найденное полученным значением значение t(теорет) с t(экспер), рассчитаем изотонический коэффициент по формуле: 𝑖= экспериментально ∆𝑡(эксп) 272.75 = = 1.004 ∆𝑡(теор) 271.54 Рассчитаем кажущуюся степень диссоциации ( ) соли из соотношения: 𝛼= (𝑖 − 1) 1.004 − 1 = = 0.004 (𝑘 − 1) 2−1 здесь k - общее число ионов, образующихся при диссоциации электролита. Определим мольную долю соли. N = n1/(n1 + n2) = 0,01/(100 + 0,01) ~ 0,0001. По закону Рауля, N = (P0 - Р)/Р0 Р0 = 3166,67 Па. 𝑃 = 𝑃0(1 − 𝑛(𝐾𝐶𝑙 ) ) 𝑛(𝐾𝐶𝑙 ) + 𝑛(𝐻2 𝑂) 1 = 0.0134 моль 74.5 100 𝑛(𝐻2𝑂) = = 5,56 моль 18 0,0134 𝑃 = 3166,67 ∙ (1 − ) = 3159 Па 0,0134 + 5,56 𝑛(𝐾𝐶𝑙 ) = Вишняков А.В., Кизим Н.Ф. Физическая химия. Учебник для ВУЗ-ов.М.: Химия, 2012, -840с., С.264)