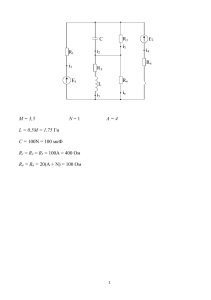
Необходимо найти минимальное значение целевой функции F = 3x 1x2 → min, при системе ограничений: -x1+x2≤4, (1) x1≥2, (2) x1+x2≥3, (3) x1-x2≤5, (4) x1 ≥ 0, (5) x2 ≥ 0, (6) Шаг №1. Построим область допустимых решений, т.е. решим графически систему неравенств. Для этого построим каждую прямую и определим полуплоскости, заданные неравенствами (полуплоскости обозначены штрихом). Построим уравнение -x1+x2 = 4 по двум точкам. Для нахождения первой точки приравниваем x1 = 0. Находим x2 = 4. Для нахождения второй точки приравниваем x2 = 0. Находим x1 = -4. Соединяем точку (0;4) с (-4;0) прямой линией. Определим полуплоскость, задаваемую неравенством. Выбрав точку (0; 0), определим знак неравенства в полуплоскости:-1 ∙ 0 + 1 ∙ 0 - 4 ≤ 0, т.е. -x1+x2 - 4≤ 0 в полуплоскости ниже прямой. Построим уравнение x1 = 2. Эта прямая проходит через точку x1 = 2 параллельно оси OX2. Определим полуплоскость, задаваемую неравенством. Выбрав точку (0; 0), определим знак неравенства в полуплоскости:1 ∙ 0 - 2 ≤ 0, т.е. x1 - 2≥ 0 в полуплоскости правее прямой. Построим уравнение x1+x2 = 3 по двум точкам. Для нахождения первой точки приравниваем x1 = 0. Находим x2 = 3. Для нахождения второй точки приравниваем x2 = 0. Находим x1 = 3. Соединяем точку (0;3) с (3;0) прямой линией. Определим полуплоскость, задаваемую неравенством. Выбрав точку (0; 0), определим знак неравенства в полуплоскости:1 ∙ 0 + 1 ∙ 0 - 3 ≤ 0, т.е. x1+x2 - 3≥ 0 в полуплоскости выше прямой. Построим уравнение x1-x2 = 5 по двум точкам. Для нахождения первой точки приравниваем x1 = 0. Находим x2 = -5. Для нахождения второй точки приравниваем x2 = 0. Находим x1 = 5. Соединяем точку (0;-5) с (5;0) прямой линией. Определим полуплоскость, задаваемую неравенством. Выбрав точку (0; 0), определим знак неравенства в полуплоскости:1 ∙ 0 - 1 ∙ 0 - 5 ≤ 0, т.е. x1-x2 - 5≤ 0 в полуплоскости ниже прямой. или Шаг №2. Границы области допустимых решений. Пересечением полуплоскостей будет являться область, координаты точек которого удовлетворяют условию неравенствам ограничений задачи. Обозначим границы области многоугольника решений. системы Шаг №3. Рассмотрим целевую функцию задачи F = 3x1-x2 → min. Построим прямую, отвечающую значению функции F = 3x1-x2 = 0. Вектор-градиент, составленный из коэффициентов целевой функции, указывает направление максимизации F(X). Начало вектора – точка (0; 0), конец – точка (3;-1). Будем двигать эту прямую параллельным образом. Поскольку нас интересует минимальное решение, поэтому двигаем прямую до первого касания обозначенной области. На графике эта прямая обозначена пунктирной линией. Прямая F(x) = const пересекает область в точке B. Так как точка B получена в результате пересечения прямых (1) и (2), то ее координаты удовлетворяют уравнениям этих прямых: -x1+x2=4 x1=2 Решив систему уравнений, получим: x1 = 2, x2 = 6 Откуда найдем минимальное значение целевой функции: F(x) = 3∙2 - 1∙6 = 0 Решение было получено и оформлено с помощью сервиса: Решение задач линейного программирования графическим методом Вместе с этой задачей решают также: Решение симплекс-методом Двойственный симплекс-метод Двойственная задача линейного программирования Метод Гомори Транспортная задача Расчет сетевого графика Динамическое программирование Теория массового обслуживания