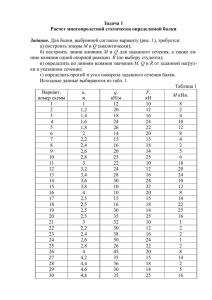
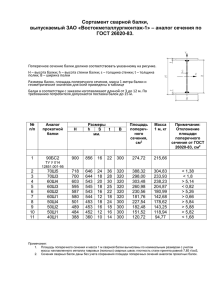
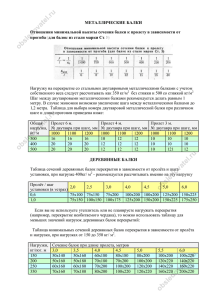
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «САМАРСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ ИМЕНИ АКАДЕМИКА С.П. КОРОЛЕВА» (САМАРСКИЙ УНИВЕРСИТЕТ) Институт авиационной и ракетно­космической техники Кафедра сопротивления материалов Расчетно­проектировочная работа «РАСЧЁТ СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ БАЛОК» Вариант №19 Выполнила студентка гр.1206 Шулепов Александр Проверил преподаватель Вакулюк В.С. САМАРА 2023 ЗАДАНИЕ Заданы схемы балок, размеры и действующие нагрузки, Требуется: 1. Построить эпюры Q и M для балок с буквенными данными; 2. Построить эпюры Q и M для балок с числовыми данными; 3. Назначить размеры поперечных сечений балок; 4. Произвести сравнительный экономический анализ различных поперечных сечений заданной балки; 5. Провести полную проверку прочности заданной балки; 6. Найти перемещение в одном из сечений заданной балки. 2 РЕФЕРАТ Расчетно-проектировочная работа 22 с, 13 рисунков, 4 источника. БАЛКА, РЕАКЦИИ ОПОР, ПОПЕРЕЧНАЯ СИЛА, ИЗГИБАЮЩИЙ МОМЕНТ, ПРОВЕРКА ПРОЧНОСТИ, ПРОГИБ, УГОЛ ПОВОРОТА Объектом исследования являются статически определимые балки. Цель работы – расчеты на прочность и жесткость статически определимых балок. В результате работы определены реакции опор, построены эпюры поперечных сил и изгибающих моментов, показан характер изогнутых осей для заданных балок. Для балок с числовыми данными подобраны двутавровые поперечные сечения. Для одной из числовых балок подобраны также поперечные сечения в виде круга, кольца, прямоугольника и проведено сравнение масс полученных сечений. Для заданной балки с двутавровым сечением проведена полная проверка прочности, определены прогиб и угол поворота в указанных сечениях. Эффективность работы заключается в выборе наиболее экономичного поперечного сечения балки. 3 СОДЕРЖАНИЕ ВВЕДЕНИЕ.................................................................................................... 5 РАСЧЁТНЫЕ СХЕМЫ И ЭПЮРЫ БАЛОК С БУКВЕННЫМИ ОБОЗНАЧЕНИЯМИ ............................................................................................... 6 РАСЧЁТНЫЕ СХЕМЫ И ЭПЮРЫ БАЛОК С ЧИСЛОВЫМИ ДАННЫМИ. ПОДБОР ДВУТАВРОВЫХ СЕЧЕНИЙ............. 9 ПОДБОР РАЗМЕРОВ ПОПЕРЕЧНЫХ СЕЧЕНИЙ ................................ 13 ПОЛНАЯ ПРОВЕРКА ПРОЧНОСТИ БАЛКИ №19 ............................... 15 НАХОЖДЕНИЕ ПЕРЕМЕЩЕНИЙ В ЗАДАННОМ СЕЧЕНИИ БАЛКИ №161 ....................................................................................................................... 19 ЗАКЛЮЧЕНИЕ ........................................................................................... 21 СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ ................................. 22 4 ВВЕДЕНИЕ В настоящее время среди деталей машин часто встречаются балочные конструкции. Поэтому необходимо уметь рассчитывать балки на прочность и жёсткость. Данная работа является актуальной, так как она позволяет получить опыт в расчёте балок на прочность, в том числе в подборе различных поперечных сечений, удовлетворяющих условию необходимой прочности. 5 РАСЧЁТНЫЕ СХЕМЫ И ЭПЮРЫ БАЛОК С БУКВЕННЫМИ ОБОЗНАЧЕНИЯМИ Рисунок 1 - Схема и эпюры балки №4 Рисунок 2 - Схема и эпюры балки №215 6 Рисунок 3 - Схема и эпюры балки №426 Рисунок 4 - Схема и эпюры балки №637 7 Рисунок 5 - Схема и эпюры балки №848 8 РАСЧЁТНЫЕ СХЕМЫ И ЭПЮРЫ БАЛОК С ЧИСЛОВЫМИ ДАННЫМИ. ПОДБОР ДВУТАВРОВЫХ СЕЧЕНИЙ. Рисунок 6 - Схема и эпюры балки №4 |𝑀|наиб 50 ∙ 103 𝑊𝑥 ≥ = = 312,5 см3 . 6 [𝜎] 160 ∙ 10 Двутавровое сечение. Принимаем двутавр №24а: 𝐴дв = 37,5 см2 ; 𝑊𝑥 = 317 см3 ; 𝐼𝑥 = 3800 см4 . 9 Рисунок 7 - Схема и эпюры балки №75 |𝑀|наиб 214,5 ∙ 103 𝑊𝑥 ≥ = = 1340 см3 . 6 [𝜎] 160 ∙ 10 Двутавровое сечение. Принимаем двутавр №50: 𝐴дв = 100 см2 ; 𝑊𝑥 = 1589 см3 ; 𝐼𝑥 = 39727 см4 . Рисунок 8 - Схема и эпюры балки №146 10 |𝑀|наиб 585 ∙ 103 𝑊𝑥 ≥ = = 3656 см3 . 6 [𝜎] 160 ∙ 10 Двутавровое сечение. Принимаем двутавр №50: 𝐴дв = 100 см2 ; 𝑊𝑥 = 1589 см3 ; 𝐼𝑥 = 39727 см4 . Рисунок 9 – Схема и эпюры балки 217 11 Рисунок 10 - Схема и эпюры балки №288 |𝑀|наиб 40 ∙ 103 𝑊𝑥 ≥ = = 250 см3 . 6 [𝜎] 160 ∙ 10 Двутавровое сечение. Принимаем двутавр №22а: 𝐴дв = 32,8 см2 ; 𝑊𝑥 = 254 см3 ; 𝐼𝑥 = 2790 см4 . 12 ПОДБОР РАЗМЕРОВ ПОПЕРЕЧНЫХ СЕЧЕНИЙ Произведём подбор для балки под номер 217. |𝜎|наиб = |𝑀|наиб ≤ [𝜎]; 𝑊𝑥 |𝑀|наиб 207,5 ∙ 103 𝑊𝑥 ≥ = = 1296 см3 . [𝜎] 160 ∙ 106 Двутавровое сечение. Принимаем двутавр №50: 𝐴дв = 100 см2 ; 𝑊𝑥 = 1589 см3 ; 𝐼𝑥 = 39727 см4 . ℎ Прямоугольное сечение ( = 2): 𝑏 𝑏 ∙ ℎ2 2 3 𝑊𝑥 = = 𝑏 ; 6 3 3 3𝑊 3 3 ∙ 1296 𝑥 𝑏=√ =√ = 12,48 см; 2 2 𝐴пр = 2𝑏 2 = 311,5 см2 . Квадратное сечение. 𝑎3 𝑊𝑥 = ; 6 3 𝑎 = 3√6 ∙ 𝑊𝑥 = √6 ∙ 1296 = 19,8 см; 𝐴кв = 𝑎2 = 392 см2 . Круглое сечение. 𝜋 ∙ 𝐷3 𝑊𝑥 = ; 32 3 32 ∙ 𝑊 3 32 ∙ 1296 𝑥 𝐷=√ =√ = 23,6 см; 𝜋 𝜋 𝐴кр 𝜋 ∙ 𝐷2 𝜋 ∙ 24,82 = = = 437 см2 . 4 4 13 Кольцевое сечение( α = d D = 0,8). 𝜋 ∙ 𝐷3 (1 − 𝛼 4 ); 𝑊𝑥 = 32 3 3 32 ∙ 𝑊𝑥 32 ∙ 1296 √ 𝐷=√ = = 28,2 см; 𝜋(1 − 𝛼 4 ) 𝜋(1 − 0,84 ) 𝐴кл 𝜋 ∙ 𝐷2 𝜋 ∙ 29,62 2 (1 − 𝛼 ) = (1 − 0,82 ) = 224,8 см2 . = 4 4 𝐴дв : 𝐴кл : 𝐴пр : 𝐴кв : 𝐴кр = 100: 224,8: 311: 392: 437 Из этого сравнения следует, что при плоском изгибе, самый экономичным является двутавровое сечение. 14 ПОЛНАЯ ПРОВЕРКА ПРОЧНОСТИ БАЛКИ №217 Проверка проводится для двутаврового поперечного сечения. Рисунок 11 – Схема балки №217 Таблица 1 – Характеристики двутавра №50 Формула для нормальных напряжений: 𝜎= |ℳ|наиб ∗ у 𝒥х Для касательных напряжений применима формула Журавского: 𝑄 ∗ 𝑆𝑥отс 𝜏= 𝒥х ∗ 𝑏(𝑦) 15 1 – опасная точка: в ней действуют самые большие для данной балки нормальные напряжения, а касательные отсутствуют. Для вычисления нормальных напряжений в этой точке нужно взять сечение с максимальным по модулю изгибающим моментом. 500 ∗ 10−3 | − 207,5| ∗ 10 ∗ 2 = = 130,6 МПа < [𝜎] = 160 МПа; −8 39727 ∗ 10 3 𝜎наиб Условие прочности выполняется 2 – опасная точка. Для этой точки характерны отсутствие нормальных напряжений и максимальное значение поперечной силы в сечении, как следствие – максимальное значение касательного напряжения. 𝜏наиб −65,9 ∗ 103 ∗ 919 ∗ 10−6 = = −15,16 МПа; 39727 ∗ 10−8 ∗ 10 ∗ 10−3 [𝜎] 160 МПа [𝜏] = = = 92,3 МПа; √3 √3 𝜏наиб < [𝜏]. Выполняется условие прочности. 3 – опасная точка. В этой точке возникают как нормальные, так и касательные напряжения. | − 207,5| ∗ 103 500 𝜎= ∗( − 15,2) ∗ 10−3 = 122,6МПа; −8 39727 ∗ 10 2 16 −65,9 ∗ 103 ∗ (919 ∗ 10−6 − 0,5 ∗ 10 ∗ 10−3 (250 − 15,2)2 ∗ 10−6 ) 𝜏= 39727 ∗ 10−8 ∗ 10 ∗ 10−3 = −10,67 МПа; 𝜎экв = √𝜎 2 + 3𝜏 2 = √122,62 + 3 ∙ 10,672 = 124 МПа < [𝜎]. Определение главных напряжений и положение главных площадок аналитическим методом в точке 3: Рисунок 12 –Расположение напряжений 2 𝜎𝐼,𝐼𝐼 = 0,5[(𝜎𝛼 + 𝜎𝛽 ) ± √(𝜎𝛼 − 𝜎𝛽 ) + 4 ∗ 𝜏𝛼2 ; 𝜎𝐼 = 0,5 ∗ (122,6 + √122,62 + 4 ∗ 10,672 ) = 123,5 МПа; 𝜎𝐼𝐼 = 0,5 ∗ (122,6 − √141,82 + 4 ∗ 10,672 ) = −0,9 МПа; 𝜎1 ≥ 𝜎2 ≥ 𝜎3 ; 𝜎1 = 123,5 МПа; 𝜎2 = 0; 𝜎3 = −0,7 МПа. Определим наклон главной площадки: 𝑡𝑔𝛼 = − 𝜏𝛼 10,67 = = 0,08; 𝜎𝛼 − 𝜎𝐼𝐼 122,6 + 0,9 𝛼 = 5°. 17 Рисунок 12 – Круг Мора 18 НАХОЖДЕНИЕ ПЕРЕМЕЩЕНИЙ В ЗАДАННОМ СЕЧЕНИИ БАЛКИ №217 Рисунок 13 – Схема балки №217 Составляем выражения изгибающего момента для произвольных сечений на каждом участке балки № 217; двутавр № 50, 𝒥х =39727 см4. ℳ(𝑧1 ) = 41,9 ∙ 𝑧1 ; 𝑧2 2 ℳ(𝑧2 ) = 85,6 ∙ 𝑧2 − 25 ∙ ; 2 Составляем дифференциальные уравнения изогнутой оси балки для каждого участка и дважды интегрируем их: 𝐸𝒥х ∗ 𝑦1′′ = 41,9 ∙ 𝑧1 ; 𝐸𝒥х ∗ 𝐸𝒥х ∗ 𝑦1 𝐸𝒥х ∗ 𝐸𝒥х ∗ 𝑦2′′ 𝑦2′ 𝑦1′ 𝑧12 = 41,9 + 𝐶1 ; 2 𝑧13 = 41,9 + 𝐶1 𝑧1 + 𝐷1 . 6 𝑧2 2 = 85,6 ∙ 𝑧2 − 25 ∙ ; 2 𝑧22 𝑧2 3 = 85,6 − 25 ∙ + 𝐶2 ; 2 6 𝑧23 𝑧2 4 𝐸𝒥х ∗ 𝑦2 = 85,6 − 25 ∙ + 𝐶2 𝑧2 + 𝐷2 . 6 24 Составляем граничные условия и, подставляя их в соответствующие уравнения, определяем постоянные интегрирования: 19 1) 𝑧1 = 0; 𝑦1 = 0; 𝑦1′ = 0 𝑧12 0 = 41,9 + 𝐶1 ; 2 𝐶1 = 0 кН ∗ м2 ; 𝑧13 0 = 41,9 + 𝐶1 𝑧1 + 𝐷1 ; 6 𝐷2 = 0 кН ∗ м2 . 2) 𝑧1 = 3; 𝑧2 = 3; 𝑦2 = 𝑦1 ; 𝑦2′ = 𝑦1′ ; 9 9 27 41,9 = 85,6 − 25 ∙ + 𝐶2 ; 2 2 6 𝐶2 = −84,15 кН ∗ м2 ; 41,9 27 27 81 = 85,6 − 25 ∙ − 84,15 ∙ 3 + 𝐷2 ; 6 6 24 𝐷2 = 140,175 кН ∗ м2 . Определим прогиб в 𝑧1 = 3: 𝑦1′ (3) 188,55 ∙ 103 = = 2,373 ∙ 10−3 рад; 2 ∙ 1011 ∙ 39727 ∙ 10−8 188,5 ∙ 103 у1 (3) = = 2,373 мм. 2 ∙ 1011 ∙ 39727 ∙ 10−8 20 ЗАКЛЮЧЕНИЕ После выполнения данной расчётно-проектировочной работы появился опыт в построении эпюр поперечных сил и изгибающих моментов в статически определимых балках, что позволяет рассчитывать балки на прочность, подбирать заданные поперечные сечения, удовлетворяющие условию необходимой прочности. Проведён сравнительный экономический анализ различных поперечных сечений заданной балки и установлено, что наиболее экономичным (с точки зрения минимальной массы) является двутавровое сечение. Появились навыки нахождения перемещений в заданном сечении балки с помощью дифференциального уравнения изогнутой оси. 21 СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ 1. Феодосьев, В.И. Сопротивление материалов: учебник для втузов [Текст] / В.И. Феодосьев. – М.: МГТУ им. Баумана, 2018. – 544 с. 2. Расчётно-проектировочные и курсовые работы по сопротивлению материалов [Текст]: учебное пособие для студентов втузов / А.С. Букатый, В.С. Вакулюк, О.В. Каранаева, [и др.]. – Самара: Изд-во Самарского университета, 2017. – 138 с. 3. СТО 02068410-004-2018. Общие требования к учебным текстовым документам [Текст]. - Самара: Изд-во Самарского университета, 2018. – 36с. 4. Расчёты брусьев на прочность и устойчивость [Текст]: учебное пособие для студентов втузов / Ю. Н. Сургутанова [и др.]. – Самара: Изд-во Самарского университета, 2017. – 112 с. 22