ФИЗИЧЕСКАЯ ХИМИЯ.
СТРОЕНИЕ ВЕЩЕСТВА
(Химическая связь и
строение молекул)
Лекция №2. Простые системы и
атом водорода
к.х.н., доц. Ткаченко Олег Юрьевич
1
I.3 ПРОСТЫЕ МОДЕЛИ В КВАНТОВОЙ МЕХАНИКЕ
В реальных системах точно решить, а иногда и составить,
уравнение Шрёдингера невозможно. Подход к решению УШ дает
изучение простых моделей (систем) – для них УШ решается точно.
•
•
•
Рассмотрим три простые системы, отвечающие трем видам
движения частицы:
поступательное – потенциальный ящик,
колебательное – осциллятор,
вращательное – ротатор.
2
I.3 ПРОСТЫЕ МОДЕЛИ В КВАНТОВОЙ МЕХАНИКЕ
ОДНОМЕРНЫЙ ПОТЕНЦИАЛЬНЫЙ ЯЩИК
Это задача об ограниченном движении частицы.
^
H ( x ) Е( x )
U=0
U
U
m
0
2
2
L
d
( x ) E( x )
2
2m dx
x
^
^
H Т ( U 0)
2 d2
H
2m dx 2
^
d2
2mE
( x ) 2 ( x ) 0
2
dx
3
I.3 ПРОСТЫЕ МОДЕЛИ В КВАНТОВОЙ МЕХАНИКЕ
ОДНОМЕРНЫЙ ПОТЕНЦИАЛЬНЫЙ ЯЩИК
Результаты решения УШ:
2
n
n (x)
sin x
L L
2 2
E n2
n
2
2mL
квантовое число nN {1, 2, 3, ...}.
4
I.3 ПРОСТЫЕ МОДЕЛИ В КВАНТОВОЙ МЕХАНИКЕ
ГАРМОНИЧЕСКИЙ ЛИНЕЙНЫЙ ОСЦИЛЛЯТОР
Это колебательная система
В классической механике
по закону Гука
F = kx
x
x
1 2
U Fdx k xdx kx
2
0
0
1
Уравнение гармонических колебаний
частота основного колебания
k 2
х a sin a sin 20
m
1 k
0
2 m
1
2
5
I.3 ПРОСТЫЕ МОДЕЛИ В КВАНТОВОЙ МЕХАНИКЕ
ГАРМОНИЧЕСКИЙ ЛИНЕЙНЫЙ ОСЦИЛЛЯТОР
^
В квантовой механике решаем УШ:
2 d2 1 2
HTU
kx ;
2
2m dx
2
H ( x ) Е( x )
d 2 2m
1 2
2 E kx 0
2
2
dx
Результаты решения УШ:
1
2a
0
1
E 0 h 0
2
2
1
ax 2
e
нулевая энергия
(энергия нулевых
колебаний)
2a 2 12 ax 2
1 2a xe ...
3
1
E1 h 0 1 h 0 ...
2
2
1
E v v h 0
2
колебательное квантовое
число v Z0 {0,1, 2, 3, ...}
6
I.3 ПРОСТЫЕ МОДЕЛИ В КВАНТОВОЙ МЕХАНИКЕ
ЖЕСТКИЙ РОТАТОР
Это система вращающихся на фиксированном расстоянии масс
приведенная масса m
r
m1
m1 m 2
m1 m 2
момент инерции ротатора I = m1r12 + m2r22 = mr2
m2
УШ с учетом U = 0:
2 IE
2m
2
2 E 0; 2 0
2
Результаты решения УШ для энергии:
E вращ
2
JJ 1,
2I
где J = 0,1,2,3...
7
II. СТРОЕНИЕ АТОМА
II.1 ОДНОЭЛЕКТРОННЫЕ СИСТЕМЫ
СХЕМА РЕШЕНИЯ УШ ДЛЯ АТОМА ВОДОРОДА
И ВОДОРОДОПОДОБНОГО ИОНА
Фундаментальное значение ТОЧНОГО решения УШ для атома водорода
(водородоподобного иона).
1. Задание модели – «картинка»
2. Составление УШ
Qe = e
Qn = Ze
me
Мn
H E
r
H T U
2
2
2
2
T Tn Тe
n
e
2M n
2m e
U U en
U U en
1 e2
40 r
1 Ze 2
40 r
(водородоподобный ион)
8
СХЕМА РЕШЕНИЯ УШ ДЛЯ АТОМА ВОДОРОДА И
ВОДОРОДОПОДОБНОГО ИОНА
3. Приближение Борна-Оппенгеймера (ПБО)
ВФ системы зависит от координат двух частиц – ядра и электрона:
H (q n , q e ) E (q n , q e );
2
2
1 e2
2
2
n
e
(q n , q e ) E(q n , q e )
2m e
40 r
2M n
Необходимо перейти к точно решаемой задаче для одной частицы в ПБО:
а) для гамильтониана
mp
me
1836
2
2
2
2
T
n
e
2M n
2m e
0
Движение ядра по сравнению с электроном настолько
медленное, что мы считаем ядро неподвижным, по отношению к
движущимся электронам.
Пренебрегаем кинетической энергией ядра по сравнению с
кинетической энергией электрона.
9
СХЕМА РЕШЕНИЯ УШ ДЛЯ АТОМА ВОДОРОДА И
ВОДОРОДОПОДОБНОГО ИОНА
б) для ВФ в приближении Борна-Оппенгеймера считаем движения
ядра и электрона независимыми:
(qn, qe) = n(qn) e(qe).
С учетом ПБО из УШ для атома водорода получим два отдельно решаемых
уравнения для ядерной и электронной частей ВФ. Решаем УШ только для
электронной части:
2
1 e2
2
e
e (q e ) E e e (q e )
40 r
2m e
Max Born;
11 декабря 1882,
Бреслау — 5
января 1970,
Гёттинген
Julius Robert
Oppenheimer,
22 апреля 1904,
Нью-Йорк —
18 февраля
1967, Принстон
10
СХЕМА РЕШЕНИЯ УШ ДЛЯ АТОМА ВОДОРОДА И
ВОДОРОДОПОДОБНОГО ИОНА
4. Переход к сферическим координатам и решение методом
разделения переменных
УШ для электронной части в системе СИ и а.с.е.:
2
1 e2
2
1
1
e
E, e 2 E, где r x e 2 y e 2 z e 2
2m e
40 r
2
r
В УШ невозможно разделить переменные в декартовых координатах,
поэтому переходят к сферическим r, , :
0r - расстояние,
(широта - полярный угол 0)
(долгота – азимутальный угол 02).
H x , y , z H r , ,
2 x ,y ,z 2 r ,,
Лапласиан в сферических координатах:
r
2
1 2
1
1
2
2 r
2
sin 2 2
r
r
r sin 2
r
r sin
11
СХЕМА РЕШЕНИЯ УШ ДЛЯ АТОМА ВОДОРОДА И
ВОДОРОДОПОДОБНОГО ИОНА
Решаем УШ методом разделения переменных, представив ВФ вместо:
(xe, ye, ze)
берем
(r, , ) = R(r)()() = R(r)Y(,),
где где R(r) - радиальная часть и Y(,)- угловая часть ВФ.
Эта подстановка даст три легко решаемых обыкновенных
дифференциальных уравнения для функций R(r), () и ().
5. Результат решения УШ
nlml (r, , ) R n ,l (r ) l,ml () ml () f (n, l, m l )
4
2
m
e
Z
e
Е n 2
2 , [Дж ] (водородоподобный ион)
2
H Е
(40 ) 2n
Е n 1 2 , [а.е.] (атом водорода Z 1)
2n
12
ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ РЕШЕНИЯ УШ.
КВАНТОВЫЕ ЧИСЛА И ИХ ФИЗИЧЕСКИЙ СМЫСЛ
Квантовые числа – номера состояний системы. Их значение и взаимосвязь
обусловлены требованиями к ВФ. Имеют смысл только для одноэлектронной
системы.
Главное квантовое число n = 1, 2, 3 … определяет квантование полной
энергии (n0, т.к. тогда Еn ):
Z2
Е n 2 f (n ), [a.e.]
2n
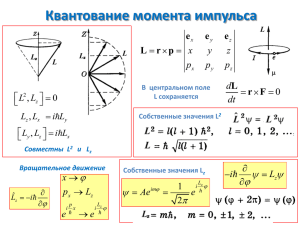
Орбитальное квантовое число l = 0, 1, 2, … (n − 1) определяет квантование
модуля вектора момента импульса электрона:
| | ( 1) ,
[ Дж с ]
Магнитное квантовое число ml = 0, ±1, ±2, …± l (всего 2l+1 значение)
определяет квантование проекции вектора момента импульса электрона на
заданную ось:
z m ,
[ Дж с]
13
СПИН
Трех квантовых чисел (трех пространственных координат) не
достаточно для описания состояния электрона, т.к. он обладает собственным
магнитным моментом, не связанным с его орбитальным движением.
Спин – вектор собственного момента импульса электрона, или 4я
координата (внутренняя степень свободы). Не имеет классического
аналога.
Формулы квантования
Модуль вектора спина | s | s(s 1) ,
где спиновое квантовое число s=1/2
(электрон с полуцелым спином)
cпин электрона | s | s(s 1)
Проекция вектора спина
3
, Дж с
2
s z ms
где спиновое магнитное квантовое число ms=1/2
14
АТОМНАЯ ОРБИТАЛЬ (АО)
Атомная орбиталь (АО) –
одноэлектронная волновая
функция, описывающая
состояние электрона в атоме,
задаваемая набором трех
квантовых чисел n, l, ml.
(Р. Малликен)
Краткая форма записи АО имеет вид:
nlm = nlm
Значение квантового чила l 0 1 2 3 4 5
Обозначение орбитали
spdfgh
Примеры: 100=1s0, 210=2p0 (2pz)
Robert Sanderson
Mulliken;
7 июня 1896, Ньюберипорт,
Массачусетс — 31 октября
1986, Арлингтон, Виргиния
15