Программа курсов учителей математики

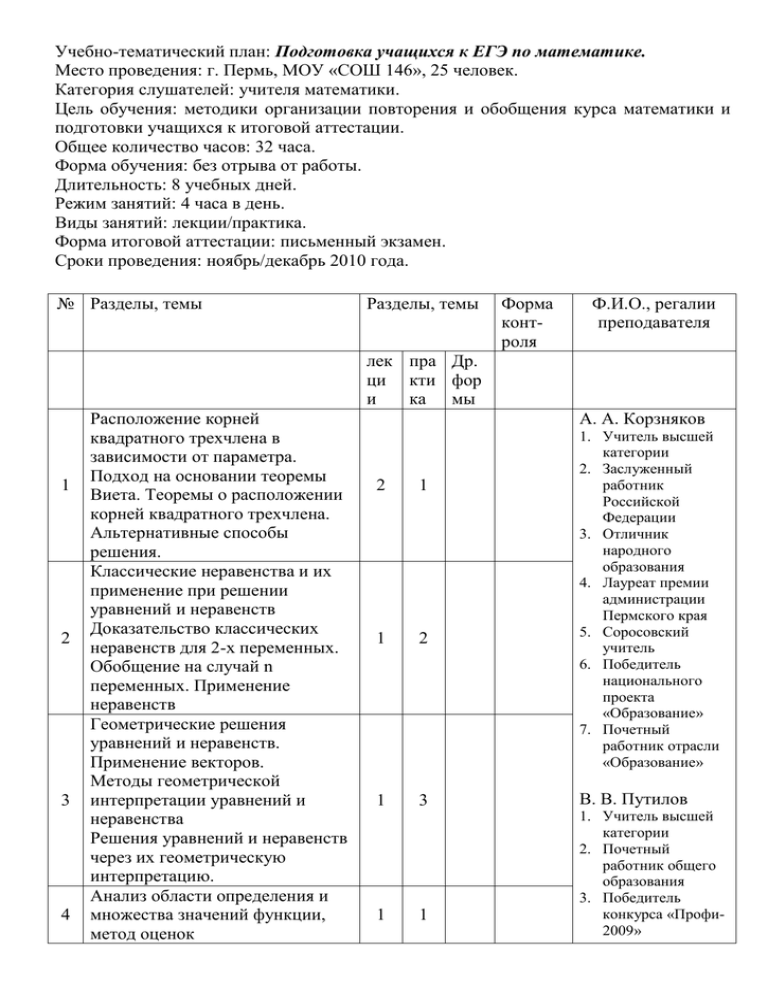
Учебно-тематический план: Подготовка учащихся к ЕГЭ по математике.
Место проведения: г. Пермь, МОУ «СОШ 146», 25 человек.
Категория слушателей: учителя математики.
Цель обучения: методики организации повторения и обобщения курса математики и
подготовки учащихся к итоговой аттестации.
Общее количество часов: 32 часа.
Форма обучения: без отрыва от работы.
Длительность: 8 учебных дней.
Режим занятий: 4 часа в день.
Виды занятий: лекции/практика.
Форма итоговой аттестации: письменный экзамен.
Сроки проведения: ноябрь/декабрь 2010 года.
№ Разделы, темы
Разделы, темы
Форма
контроля
Ф.И.О., регалии
преподавателя
лек пра Др.
ци кти фор
и
ка мы
1
2
3
4
Расположение корней
квадратного трехчлена в
зависимости от параметра.
Подход на основании теоремы
Виета. Теоремы о расположении
корней квадратного трехчлена.
Альтернативные способы
решения.
Классические неравенства и их
применение при решении
уравнений и неравенств
Доказательство классических
неравенств для 2-х переменных.
Обобщение на случай n
переменных. Применение
неравенств
Геометрические решения
уравнений и неравенств.
Применение векторов.
Методы геометрической
интерпретации уравнений и
неравенства
Решения уравнений и неравенств
через их геометрическую
интерпретацию.
Анализ области определения и
множества значений функции,
метод оценок
А. А. Корзняков
2
1
1
2
1
3
1
1
1. Учитель высшей
категории
2. Заслуженный
работник
Российской
Федерации
3. Отличник
народного
образования
4. Лауреат премии
администрации
Пермского края
5. Соросовский
учитель
6. Победитель
национального
проекта
«Образование»
7. Почетный
работник отрасли
«Образование»
В. В. Путилов
1. Учитель высшей
категории
2. Почетный
работник общего
образования
3. Победитель
конкурса «Профи2009»
5
6
7
8
Идеи метода оценок (метода
мажорант). Примеры.
Решение уравнений и неравенств
с использованием анализа
области определения и области
значений входящих в уравнение
функций.
Симметрия уравнений и ее
применение. Четность функций
Использование симметрии
уравнений и, в частности,
четности (нечетности) входящих
в него функций для решения
задач.
Применение симметрии
уравнений. Задачи с
параметрами.
Использование монотонности
функций.
Монотонность функций и
количество решений. (упрощение
уравнений при наличии
монотонных функций).
Уравнения с итерациями и
обратными функциями.
Использование монотонности
функций в решении задач.
Планиметрия в ЕГЭ (задачи типа
C4).
Задачи с неоднозначной
конфигурацией. Типовые задачи,
связанные с окружностями.
Решение задач (на примере
пособий по подготовке к ЕГЭ)
Делимость и задачи на делимость
в ЕГЭ (задачи типа С6).
НОД, НОК и связанные вопросы.
Алгоритм Евклида. Диофантовы
уравнения.
Задачи на указанные темы.
Всего:
А. М. Бурштейн
1. Учитель высшей
категории
2. Отличник
народного
образования
3. Соросовский
учитель
4. Победитель
национального
проекта
«Образование»
1
3
1
3
2
6
1
3
10
22
Письме
нный
экзамен
-Ресурсное обеспечение программы
Компьютерный класс с выходом в интернет.
Лекционное оборудование (проектор, экран, звуковое оборудование).
Беспроводная сеть (для подключения ноутбуков/нетбуков слушателей).
-Списки используемой и рекомендуемой литературы по предмету.
1. АзаровА.И., Барвенов С.А. Функциональный и графический методы решения
экзаменационных задач. Минск. Аверсэв, 2004
2. Александров Б.И., Максимов В.П., Лурье Н.В., Колесниченко А.В., Пособие по
математике для поступающих в ВУЗы, М., МГУ, 1972
3. Алфутова Н.Б., Устинов А.В., Алгебраи теория чисел. Сборник задач. М., МЦНМО,
2005
4. Квант. Материалы вступительных экзаменов в ВУЗы. Материалы вступительных
работ в СУНЦ МГУ и ЗФТШ МФТИ.
5. Козко А.И., Чирский В.Г. Задачи с параметрами, МЦМНО, 2007
6. Колесникова С.И. Математика. Интенсивный курс подготовки к ЕГЭ. М., Айрис –
пресс, 2004
7. Колесникова С.И. Математика. Решение сложных задач ЕГЭ, М., Айрис-пресс, 2005
8. Кравцев С.В., Макаров Ю.Н., Максимов В.Ф., Нараленков М.И., Чирский В.Г.
Методы решения задач по алгебре, от простых до самых сложных. М., Экзамен,
2005г.
9. Математика в школе, Варианты вступительных экзаменов в ВУЗы.
10. Материалы Соросовских математических олимпиад.
11. Нестеренко Ю.В., Олехник С.Н., Потапов М.К. Задачи вступительных экзаменов по
математике, М., Наука, 1986, 1995г.
12. Нестеренко Ю.В., Олехник С.Н., Потапов М.К. Конкурсные задачи по математике,
М., Наука, 1992г.
13. Олехник С.Н., Потапов М.К., Пасиченко П.И. Нестандартные методы решений
уравнений и неравенств, М., МГУ, 1991г.
14. Родионов Е.M. Математика. Решение задач с параметрами. Пособие для
поступающих в ВУЗы., М., Издательство НЦ ЭНАС, 2006
15. Сборники по подготовке к ЕГЭ Клово А.Г.
16. Сборники по подготовке к ЕГЭ под ред. Лысенко Ф.Ф.
17. Сборники подготовительных задач к ЕГЭ по новой модели (ред. Семенов А.Л.,
Ященко И.В.)
18. Сивашинский И.Х. Неравенства в задачах, М., Наука, 1967
19. Соминский И.С., Элементарная алгебра. Дополнительный курс. М., Наука, 1967
20. Ткачук В.В. Математика – абитуриенту. М., МЦНМО, 1998
21. Черкасов О.Ю., Якушев А.Г. Математика для поступающих в серьезные ВУЗы, М.,
Московский лицей, 1998
22. Шарыгин И.Ф. Решение задач. Учебное пособие для 10 класса. М., Просвещение,
1994
23. Шарыгин И.Ф., Голубев В.И. Решение задач. Факультативный курс для учащихся 11
класса, М., Просвещение, 1991.