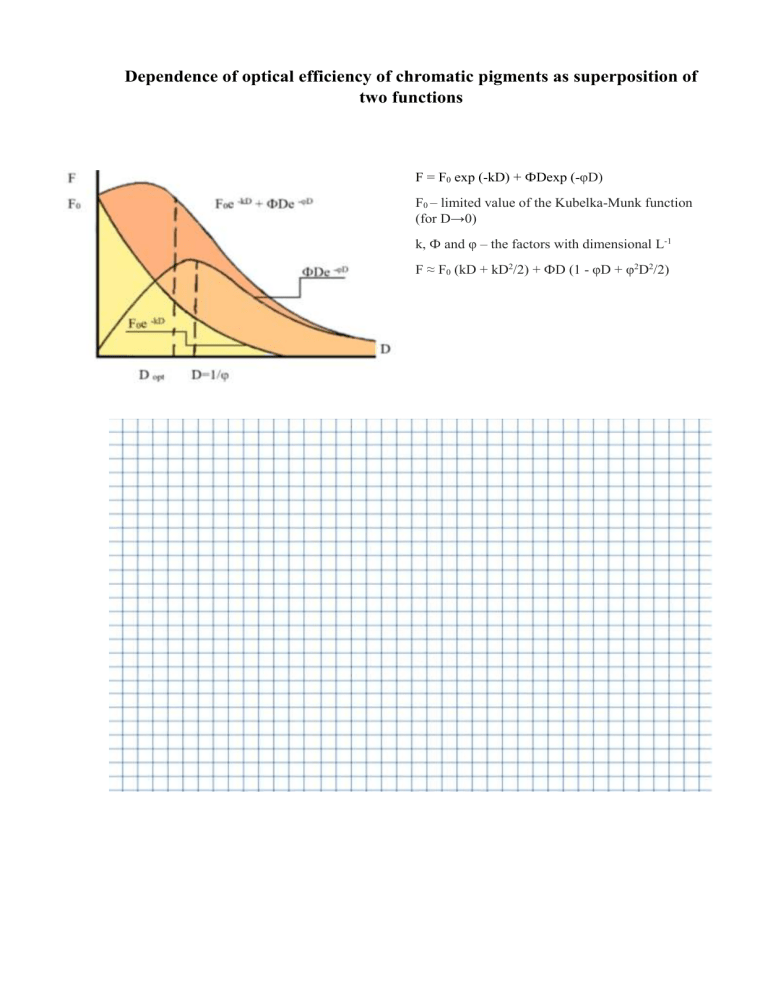
Dependence of optical efficiency of chromatic pigments as superposition of two functions F = F0 exp (-kD) + ФDexp (-φD) F0 – limited value of the Kubelka-Munk function (for D→0) k, Ф and φ – the factors with dimensional L-1 F ≈ F0 (kD + kD2/2) + ФD (1 - φD + φ2D2/2) Influence of the particle size on coloring power some chromatic pigments Influence of dispersivwness on change of cromaticity of some pigments 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. Lead yellow Lead lemon Lead orange Molybdate red Chrome red Iron-oxid red Iron minium Iron-oxid yellow Cadmium red Cadmium lemon Prussian blue Ultramarine Cobalt blue Factors of the equation F = F0 exp (-kD) + ФD exp (-φD) end the optimum particles sizes of some chromatic pigments Without coloured undertone My = 100 log (100/y) Contribution of the coloured undertone dM = 100 (log Xn/X – log Zn/Z) blue dM > 0 brown dM < 0 Кинетика процесса диспергирования F = kt – kFt / F∞ Где F – функция Кубелки-Мунка t – время процесса k – константа скорости диспергирования F∞ – функция Кубелки-Мунка для бесконечной длительности процесса Particle sizes distribution of titanium dioxide dispersion in the polyester solution Dependence of the polyester solution viscosity on the mass fraction Производительность, время и сопротивление диспергированию G = Cpk (1 - α)/αF∞ G = Cp (1 - α)/αt0,5 t = αF∞/(1 - αk) Grinding resistance (GR ≡ t0,5) t0,5 = F∞/k Cop = (k1C2 – k2C1)/2(k1 – k2) Типичные зависимости ζ-потенциала от pH







