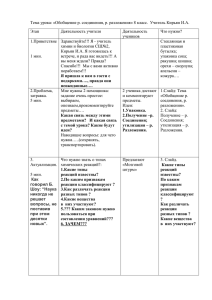
ЗАДАНИЕ № 2 Найти пятый член разложения бинома ( 𝑎 √ + 𝑥 √𝑥 𝑛 ) , 𝑎 если отношение коэффициента третьего члена к коэффициенту второго члена равна РЕШЕНИЕ: 𝑛! второй биноминальный коэффициент С1𝑛 = 1!(𝑛−1)! 𝑛! Третий биноминальный коэффициент С2𝑛 = 2!(𝑛−2)! С2 По условию имеем: С𝑛1 = 𝑛 𝑛! 2!(𝑛−2)! 𝑛! 1!(𝑛−1)! = 1!(𝑛−1)! 2!(𝑛−2)! 11 = 2 N=12 Получаем пятый член разложения по формуле: 𝑇𝑘+1 = 𝐶𝑛𝑘 𝑎𝑛−𝑘 𝑏 𝑘 𝑇5 = 4 𝑥 𝑎 8 𝑎4 ) ( ) = 485 2 𝑎 𝑥 √𝑥 4 √ 𝐶12 ( Ответ: 𝑇5 = 485 𝑎4 𝑥2 11 2