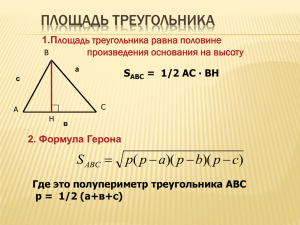
Открытый урок по геометрии Сближение теории с практикой дает самые благотворные результаты, и не одна практика от этого выигрывает, сами науки развиваются под ее влиянием. Чебышев П.Л. Глубокое и прочное усвоение школьниками основ курса математики чрезвычайно важно для формирования их математической культуры, при которой у них создаются предпосылки к активному применению математических знаний, развитию предметной культуры, творческому анализу задач, отражающих нашу реальность, производство, саму жизнь. Конспект урока геометрии в 8 классе по теме «Решение задач на вычисление площадей фигур» Цели урока: обучающие: проверка знания учащимися формул для вычисления площадей параллелограмма, треугольника, трапеции и применение формул нахождения площадей фигур к решению практических задач; развивающие: выдвижение гипотез, способов решения задачи, перенос знания в новую ситуацию, умение планировать свою деятельность; воспитательные: формирование ответственного отношения к труду, развитие активной жизненной позиции и культуры математической речи, познавательного интереса к предмету, ориентация учащихся на профессию строителя. Задачи урока: проверить знание учащимися формул площади многоугольников; применение формул для вычисления площадей параллелограмма, треугольника и трапеции при решении практических задач, в нестандартных ситуациях; показать прикладное значение материала изучаемой темы. Тип урока: обобщения и применения знаний. Формы работы: фронтальная, групповая. Методы обучения: частично - поисковый. Урок составлен по технологии креативного урока. Ход урока. Этапы Деятельность учителя урока 1. Моти Приветствие учащихся. Вступительное слово учителя. вация Добрый день! Присаживайтесь, пожалуйста. Ребята, к сегодняшнему уроку вы должны были повторить формулы нахождения площадей фигур. Давайте их вспомним. Ко всем многоугольникам подберите формулы для вычисления их площади. Как вы полагаете, для чего они вам могут пригодиться? Правильно, на уроке мы будем применять эти формулы к решению практических задач. А как вы думаете в какой области решаются практические задачи на нахождение площади? Правильно, в строительстве. Итак, тема урока «Площади многоугольников». Запишем её в тетради. Но урок у нас сегодня необычный и проходить он будет в форме игры «Строитель». 2. Содер жательна я часть урока Ребята, давайт попробуем себя в роли строителей. Конкретно наша помощь будет заключаться в выполнении расчётов по настилке паркетного пола в игровом зале размером 5,75м ×8м, то есть с помощью паркетных плиток различной формы выложить прямоугольник. Паркетные плитки имеют форму прямоугольных треугольников, параллелограммов и равнобедренных трапеций. Размеры плиток в метрах указаны на доске (Приложение 2) (работа в парах). Деятельность ученика Учащиеся называют формулы для нахождения площади фигур, представленных в таблице (Приложение 1) Ответы детей Ответы детей Записывают в тетрадь тему урока Каждая пара приступает к практическим вычислениям. Паркет укладывается в ряды так, что параллелограммы и трапеции чередуются, а треугольников в одном ряду всего два. Подсчёты показывают, что в одном ряду по ширине укладывается по 2 треугольника и по 8 параллелограммов и трапеций. Действительно, площадь одной полосы шириной 0,2 м и длиной 5,75 м будет 1,15 м2. Если площадь двух треугольников 0,03 м2, а площадь параллелограмма или трапеции 0,07 м2, то в одной полосе по ширине игрового зала поместится по 8 параллелограммов и трапеций: (1,150,03):0,07=16. Таких полос в длине комнаты поместится 8:0,2=40. Следовательно, для настилки пола понадобится 2*40=80 треугольников и по 8*40=320 параллелограммов и трапеций. Проверкой устанавливается: площадь игрового зала 5,75*8=46 м2, площадь одной полосы 5,75*0,2=1,15 м2, а таких полос 40, поэтому 1,15*40=46м2 – площадь паркетного пола. Учащиеся из каждой пары дают объяснения учителю, как они вычислили нужное количество паркетных плиток. 3. Пси хологичес кая разгрузка Понятие площади и в науке и на практике использовалось с незапамятных времён. В древности считалось, что площадь четырехугольника, последовательные стороны которой имеют длины a, b,c, d, можно вычислять по формуле (т. е. полусумму длин противоположных сторон умножить на полусумму двух других сторон). Эта формула верна только для прямоугольников. По-видимому, в древности приходилось рассматривать лишь участки, мало отличающиеся от прямоугольника по форме, а для таких участков погрешность, вносимая указанной формулой, невелика. Лишь в последствии было полностью развито учение о площадях и получены точные формулы для вычисления площади прямоугольника, параллелограмма, треугольника и других многоугольников. 4. Голо воломка. Интеллек туальная разминка (Приложение 3) Ответ: треугольник, параллелограмм, ромб. Назовите букву, стоящую в скобках, соответствующую истинному высказыванию (буквы записать на доске). 1) Ромб – это четырёхугольник, у которого… - диагонали равны и точкой пересечения делятся пополам (Б) - диагонали взаимно перпендикулярны и точкой пересечения делятся Учащиеся разгадывают математические ребусы. Л пополам (Л) - противоположные углы равны и противоположные стороны параллельны (У) 2) Параллелограмм, это четырёхугольник, у которого… - углы равны (Р) Ь - стороны равны (З) - противолежащие стороны параллельны (Ь) 3) Квадрат – это… - параллелограмм с равными сторонами (Я) - параллелограмм, у которого все углы прямые (Н) - прямоугольник, у которого все стороны равны (О) 4) Любой ромб является… - квадратом (Ю) О - прямоугольником (Е) А - параллелограммом (А) 5) Диагонали равны у … - трапеции (С) - прямоугольника (Щ) Щ - ромба (Х) 6) Любой прямоугольник является … - ромбом (В) - квадратом (И) - параллелограммом (П) П 7) Диагонали пересекаются под прямым углом у … - параллелограмма (Т) - квадрата (Д) - прямоугольника (У) Д - Из записанных слов составьте слово. (Площадь) Работа в группах. Класс делится на Учащиеся из каждой 5. Соде команды, каждая получает команды дают объяснения ржательн две учителю, как они решали ая часть карточку с заданиями. каждую задачу. урока. Задачи для 1 команды. 1) Вычислите площадь квадрата, у которого диагональ 4√2см. 2) Сторона треугольника равна 6 см, а высота, проведенная к ней, в 2 раза больше стороны. Найдите площадь треугольника. 3) Стороны параллелограмма равны 6 см и 8 см, а угол между ними равен 300. Найдите площадь параллелограмма. 4) В параллелограмме высоты равны 10 см и 5 см, площадь параллелограмма равна 60 см2 . Найдите стороны параллелограмма. Задачи для 2 команды. 1) Вычислите площадь ромба, диагонали которого 3√2см и 4√2см. 2) В трапеции основания равны 6 см и 10 см, а высота равна полусумме длин оснований. Найдите площадь трапеции. 3) Стороны треугольника равны 6 см и 8 см, а угол между ними равен 300. Найдите площадь параллелограмма. 6. Резю ме учителя 4) В параллелограмме стороны равны 14 см и 8см, высота, проведенная к большей стороне, равна 4см. Найдите площадь параллелограмма и вторую высоту. 1. Ребята, какие формулы нахождения площади мы сегодня повторили? 2. А пригодятся ли вам полученные на уроке умения вычислять площади фигур в жизни? 3. Какова была цель сегодняшнего урока? 4. Достигли ли мы её? Ответы детей Домашнее задание: п. 122-124, 126 (правила), формулы (в тетради) учить, решить задачу. Формулировку задачи вы можете найти на сайте школы в разделе «Для учащихся» Задача: В треугольнике ABC BC=34см. перпендикуляр MN, проведенный из середины BC к прямой AC, делит сторону AC на отрезки AN=25см и NC=15см. Найдите площадь треугольника ABC. Используемая литература 1. Атанасян Л. С. Геометрия 7 – 9. Учебник для 7 – 9 классов средней школы. М., «Просвещение», 2010. 2. «История математики с древнейших времѐн до начала XIXстолетия», под редакцией Ю. П. Юшкевича., М., «Наука», 1970г. Приложения Приложение 1 Приложение 2 Приложение 3