Входная диагностика для 10 класса

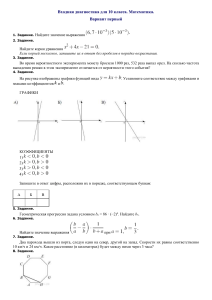
Входная диагностика для 10 класса. Математика.
Вариант первый
1. Задание.
Найдите значение выражения
2. Задание.
Найдите корни уравнения
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
3. Задание.
Во время вероятностного эксперимента монету бросили 1000 раз, 532 раза выпал орел. На сколько частота
выпадения решки в этом эксперименте отличается от вероятности этого события?
4. Задание.
На рисунке изображены графики функций вида
знаками коэффициентов и
. Установите соответствие между графиками и
ГРАФИКИ
КОЭФФИЦИЕНТЫ
1)
2)
3)
4)
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
А
Б
В
5. Задание.
Геометрическая прогрессия задана условием bn = 86 · (−2)n. Найдите b5.
6. Задание.
Найдите значение выражения
при
7. Задание.
Два парохода вышли из порта, следуя один на север, другой на запад. Скорости их равны соответственно
10 км/ч и 24 км/ч. Какое расстояние (в километрах) будет между ними через 3 часа?
8. Задание.
ABCDEFGH — правильный восьмиугольник. Найдите угол CBH. Ответ дайте в градусах.
9. Задание.
Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB = BC и
∠ABC = 49°. Найдите величину угла BOC. Ответ дайте в градусах.
10. Задание.
Найдите площадь прямоугольника, если его периметр равен 102, а отношение соседних сторон равно 2:15.
11. Задание.
На клетчатой бумаге с размером клетки 1х1 отмечены три точки:
расстояние от точки до середины отрезка
.
,
и
. Найдите
12. Задание.
Какие из следующих утверждений верны?
1. Площадь ромба равна произведению его стороны на высоту, проведённую к этой стороне.
2. Боковые стороны любой трапеции равны.
3. Один из углов треугольника всегда не превышает 60 градусов.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Повышенный уровень
13. Задание.
Решите систему уравнений
14. Задание.
Имеется два сплава с разным содержанием золота. В первом сплаве содержится 35% золота, а во втором –
60%. В каком отношении надо взять первый и второй сплавы, чтобы получить из них новый сплав, содержащий
40% золота?
15. Задание.
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 150°,
а CD = 26.
16. Задание.
В параллелограмме ABCD диагонали AC и BD пересекаются в точке K. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника AKD.
Вариант второй
1. Задание.
Найдите значение выражения
2. Задание.
Решите уравнение
3. Задание.
В группе из 20 российских туристов несколько человек владеют иностранными языками. Из них пятеро
говорят только по-английски, трое только по-французски, двое по-французски и по-английски. Какова вероятность того, что случайно выбранный турист говорит по-французски?
4. Задание.
Установите соответствие между функциями и их графиками.
ФУНКЦИИ
А)
Б)
В)
ГРАФИКИ ФУНКЦИЙ
1)
2)
3)
В таблице под каждой буквой укажите соответствующий номер.
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
A
Б
В
5. Задание.
Фигура составляется из квадратов так, как показано на рисунке: в
каждой следующей строке на 8 квадратов больше, чем в предыдущей. Сколько квадратов в 16-й строке?
6. Задание.
Найдите значение выражения
при
7. Задание.
Лестница соединяет точки A и B и состоит из 20 ступеней. Высота каждой ступени равна 16,5 см, а длина
— 28 см. Найдите расстояние между точками A и B(в метрах).
8. Задание.
В треугольнике
угол
равен 90°,
,
. Найдите
.
9. Задание.
Треугольник ABC вписан в окружность с центром в точке O. Точки O и C лежат в
одной полуплоскости относительно прямой AB Найдите угол ACB, если угол AOBравен 59°. Ответ дайте в
градусах
10. Задание.
Найдите площадь прямоугольника, если его периметр равен 60, а отношение соседних сторон равно 4:11.
11. Задание.
На клетчатой бумаге с размером клетки 1х1 изображён прямоугольный треугольник. Найдите длину его
большего катета.
12. Задание.
Какие из следующих утверждений верны?
1) Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то
такие треугольники равны.
2) Средняя линия трапеции параллельна её основаниям.
3) Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов.
Если утверждений несколько, запишите их номера в порядке возрастания.
13. Задание.
Решите уравнение
14. Задание.
Свежие фрукты содержат 93% воды, а высушенные — 16%. Сколько сухих фруктов получится из 252 кг
свежих фруктов?
15. Задание.
В трапеции АВСD боковые стороны AB и CD равны, СН — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 16, а меньшее основание BCравно
6.
16. Задание.
В треугольнике ABC с тупым
ки A1BC1 и ABC подобны.
углом ABC проведены
высоты AA1 и CC1.
Докажите,
что
треугольни-