mkt

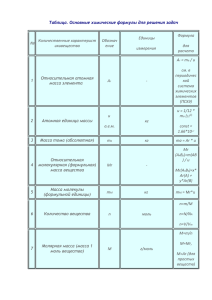
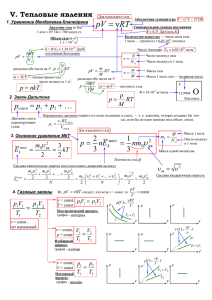
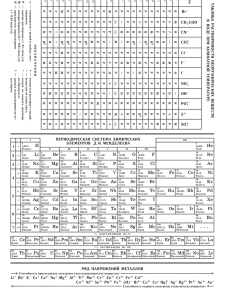
Дистанционная подготовка Abitu.ru
ФИЗИКА
Статья №9. Модель идеального газа.
Теоретический материал.
В этой статье мы рассмотрим элементы молекулярно-кинетической теории (далее – МКТ).
Напомним основные формулы, которые вводятся в МКТ при рассмотрении веществ.
1.  
N
, где  – количество вещества (размерность – моль), N A  6, 02 1023 моль1 – постоянная Авогадро,
NA
N – количество молекул в веществе (безразмерная величина).
Моль любого вещества содержит одно и то же число молекул. Это число – постоянная Авогадро.
2.   m0  N A , где  – молярная масса вещества (размерность –
кг
).
моль
Для определения молярной массы обычно используют таблицу периодической системы элементов
Д. И. Менделеева. Например, для углерода  C  12 а.е.м. соответствует молярной массе   12 10 3
3. N 
m
, где m – масса вещества, m0 – масса одной молекулы.
m0
4.  
кг
.
моль
m
.

Чаще всего в задачах веществом будет газ.
Идеальный газ – газ, для которого взаимодействием и размерами молекул можно пренебречь.
Основным уравнением, описывающим поведение идеального газа, является уравнение Менделеева-Клапейрона
(уравнение состояния идеального газа):
p V    R  T ,
где p – давление газа, V – объём, занимаемый газом,  – количество моль газа, T – абсолютная температура
газа (размерность – К ), R  8,31
Дж
– универсальная газовая постоянная.
моль  К
Очень часто в задачах мы будем считать данный нам газ идеальным.
Напомним основные формулы, справедливые для идеального газа.
1. E 
R
Дж
3
 1,38  10 23
– постоянная Больцмана, E – средняя кинетическая энергия
kT , где k 
2
NA
К
поступательного движения одной молекулы газа.
2. p  nkT , где n 
3. u 
4.  
N
– концентрация газа.
V
3kT
, где u – средняя квадратичная скорость теплового движения молекул газа.
m0
p
, где  – плотность газа.
RT
Часто над идеальным газом будут проводить различные процессы.
Процессы, протекающие при постоянном количестве  газа и неизменном значении одного из параметров
(давления p , объёма V или температуры T ), называют изопроцессами. Виды таких процессов:
1. Изотермический процесс ( T  const и   const ).
2. Изохорный (изохорический) процесс ( V  const и   const ).
3. Изобарный (изобарический) процесс ( p  const и   const ).
Для изотермического процесса справедлив закон Бойля-Мариотта: pV  const . Для изохорного процесса
справедлив закон Шарля:
p
V
 const . Для изобарного процесса справедлив закон Гей-Люссака:  const .
T
T
При описании процессов часто приходится иметь дело не только с одним газом, а со смесью N газов.
Закон Дальтона утверждает о том, что давление смеси газов, химически не взаимодействующих между собой,
равно сумме давлений (парциальных давлений) каждого из компонентов смеси:
p  p1  p2  p3  ...  pN .
При этом парциальное давление каждой из компонент смеси подчиняется уравнению Менделеева-Клапейрона:
p1V   1RT , p2V   2 RT , , pNV   N RT ,
где V – объём смеси, T – её температура.
Рассмотрим несколько примеров решения задач.
Примеры решения задач.
Пример 1.
Сосуд разделён подвижным поршнем на объёмы V 3 и 2V 3 , содержащие идеальный
газ температуры T (рис.1). До какой температуры T1 нужно нагреть газ слева от поршня,
чтобы отношение объёмов стало обратным? Справа температура газа поддерживается
постоянной.
рис.1
Решение:
Пусть  1 – количество газа в сосуде слева от поршня,  2 – количество газа в сосуде справа от поршня.
V
2V
  1  R  T , p1 
  2  R  T , откуда
3
3
2V
  1  R  T1 ,
получаем, что  2  2 1 . Уравнения состояния для газа слева и справа после нагревания: p 2 
3
V
p2    2  R  T , откуда получаем, что T1  4T .
3
Уравнения состояния для газа слева и справа до нагревания: p1 
Ответ:
T1  4T .
Пример 2. [Пенкин М.А.]
В результате изобарического расширения   4 моль идеального газа средняя квадратичная скорость молекул
этого газа увеличилась на 2% от первоначального значения скорости. Насколько расширился газ? Первоначально
газ находился при температуре T  27 0 С и нормальном атмосферном давлении.
Указание:
1 x  1
1
x при малых значениях x .
2
Решение:
Дано: T  300 K , p  105 Па , количество газа   4 моль , первоначальная среднеквадратичная скорость


3R T   T 
3RT
T

 u   1 
 1  .


T


u
T
T
Поскольку
тоже мало, значит, u  u 
(1). Из уравнения состояния идеального
 0, 02 мало, то и
u
T
2T
 R T
газа следует, что p V   R T , откуда V 
(2). Из уравнений (1) и (2) получаем, что
p
u
3RT
. Изменение среднеквадратичной скорости: u 

V 
2 RT u

4л .
p
u
Ответ:
V 
2 RT u

4л.
p
u
Пример 3.
Найти среднюю молярную массу  ср смеси газов с молярными массами 1  4 г / моль и  2  16 г / моль . Масса
первого газа в два раза больше массы второго.
Решение:
Для газа с молярной массой 1  4 г / моль : p1  V 
p2  V 
m2
m  m2
RT . Для смеси этих газов: pсмеси  V  1
RT . По закону Дальтона pсмеси  p1  p2 , значит,
2
 ср
 p1  p2   V
Значит,
m1
RT . Для газа с молярной массой  2  16 г / моль :
1

m
m
m1  m2
RT . Левую часть уравнения преобразуем:  p1  p2  V  p1  V  p2  V  1 RT  2 RT .
 ср
1
2
m  m2
m
m1
m
m  m2
. По условию 1  2 , значит, m1  2m2 .
RT  2 RT  1
RT , следовательно, ср  1
m1 m2
1
2
 ср
m2

1  2
Следовательно, ср 
Ответ:
ср 
2m2  m2
31  2
1

 5 г / моль .
2m2 m2 2  2  1
3

1
2
31 2
1
 5 г / моль .
2  2  1
3
Пример 4. [МФТИ 1998]
Чему равна масса m азота, которая содержится в воздухе комнаты объёма V  75 м 3 . Средняя квадратичная
скорость молекул азота u  500 м / с . Считать, что воздух состоит из азота и кислорода. Концентрация молекул
азота в 4 раза больше концентрации молекул кислорода. Атмосферное давление p  105 Па .
Решение:
Пусть  – молярная масса азота, p1 – парциальное давление азота, p 2 – парциальное давление кислорода.
По условию задачи воздух – смесь азота и кислорода. По закону Дальтона: p  p1  p 2 . Азот и кислород считаем
идеальными газами. Т.к. концентрация азота в 4 раза больше концентрации кислорода, то
p1
 4 , откуда
p2
p1 
m
p V 4 pV
4p
. Из уравнения состояния азота: p1V  RT , т.е. m  1

. Температуру T выражаем через
5

RT
5 RT
среднюю квадратичную скорость молекул азота u 
Следовательно: m 
Ответ:
m
 u2
3RT
, откуда T 
.
3R

12 pV
, m  72 кг .
5u 2
12 pV
 72 кг .
5u 2
Пример 5.
Объём воздушного шара равен V  224 м3 , масса оболочки M  145 кг . Шар наполнен горячим воздухом. В
нижней части оболочки имеется отверстие, через которое воздух в шаре сообщается с атмосферой. Температура
воздуха вне оболочки T0  00 C , атмосферное давление p0  105 Па . При какой минимальной температуре
воздуха внутри оболочки шар начинает подниматься? Молярную массу воздуха принять равной   29 г / моль .
Решение:
Пусть FA – сила Архимеда, действующая на воздушный шарик. Тогда шарик будет подниматься при условии, что
FA   m  M   g , где m – масса воздуха внутри шарика. Воздух вне и внутри шарика будем считать идеальным
газом. В нижней части оболочки имеется отверстие, через которое воздух в шаре сообщается с атмосферой,
значит, давление внутри шарика такое же, как и снаружи. Из уравнения состояния для воздуха внутри шарика
p0   V
. Выразим FA . По определению FA  0 gV , где 0 – плотность воздуха вне шарика.
R T
p 
p    g V
Из уравнения состояния для воздуха вне шарика получаем, что  0  0
. Итак, FA  0
,
R  T0
R  T0
получаем, что m 
следовательно,
Ответ:
1
p0    g V  p0   V


 M   g , откуда Tmin 
, Tmin  553 К .
1
MR
R  T0
 R T


T0 p0 V
Tmin 
1
 553 К .
1
MR

T0 p0 V
Пример 6. [МФТИ 1994]
В горизонтально расположенной трубке столбиком ртути длиной l  12 см заперт слой
воздуха толщиной L  35 см (рис.2). Если трубку повернуть один раз открытым концом
вниз, а другой раз вверх, то столбик ртути смещается. Разность величин этих смещений
от начального горизонтального положения равна d  2 см . При повороте трубки ртуть
рис.2
из неё не выливается. Найти величину наружного давления (в мм ртутного столба).
Решение:
Обозначим за H внешнее давление воздуха (в мм рт. ст.). Воздух будем считать идеальным газом, температура
которого в нашем опыте не изменяется.
● Повернём трубку открытым концом вниз. Давление газа уменьшится, объём газа увеличится, поэтому столбик
ртути должен опуститься. Пусть столбик ртути сместится на x1 . Тогда по закону Бойля-Мариотта
 gHSL  (  gH   gl ) S ( L  x1 ) , где  – плотность ртути, S – площадь поперечного сечения трубки, откуда
HL  ( H  l )( L  x1 ) и x1 
HL
Ll
L
.
(H  l )
(H  l)
● Повернём трубку открытым концом вверх. Давление газа увеличится, объем газа уменьшится, поэтому столбик
ртути должен подняться. Пусть столбик ртути сместится на x1 . Тогда по закону Бойля-Мариотта
 gHSL  (  gH   gl ) S ( L  x2 ) , откуда HL  ( H  l )( L  x2 ) и x2  L 
По условию x1  x2  d . Значит,
Ответ:
H  l  1
HL
Ll

.
(H  l) (H  l)
Ll
Ll
2 Ll 2
2L

d 
 d  H  l  1
, H  720 мм рт. ст.
2
2
( H  l ) (H  l )
d
(H  l )
2L
 720 мм рт. ст.
d
Домашнее задание.
Задача 1. Сосуд разделён подвижным поршнем на объёмы 2V 5 и 3V 5 ,
содержащие идеальный газ температуры T  300 К (рис.3). Как и насколько нужно
изменить температуру газа справа от поршня, чтобы отношение объёмов стало
равным? Слева температура газа поддерживается постоянной.
Задача 2. [МФТИ 1997] Моль гелия нагревается при постоянном объёме V0  400 л
так, что относительное увеличение его давления составило  
рис.3
p
 0, 4% .
p0
1) На сколько градусов T увеличилась температура газа, если его начальная температура T0  500 К ?
2) На сколько атмосфер увеличилось давление газа?
Задача 3. [МФТИ 2000] Имеется Г – образная тонкая трубка постоянного внутреннего
сечения и общей длиной 3L=1260 мм. Между слоем воздуха длиной L=420 мм и
атмосферой находится слой ртути той же длины L (рис.4).
Какой длины слой ртути останется в трубке, если вертикальное колено повернуть на 1800,
расположив его открытым концом вниз?
Внешнее давление p0  735 мм рт.ст.
рис.4
Задача 4. Сосуд ёмкостью 2V разделён пополам полупроницаемой перегородкой. В
одну половину сосуда введён водород массой m В и азот массой m А , в другой половине вакуум. Через
перегородку может диффундировать только водород. Во время процесса температура T поддерживается
постоянной. Какие давление установятся в обеих частях сосуда?
4 ноября 2009 г.
Межвузовский центр воспитания и развития
талантливой молодежи в области
естественно-математических наук
"Физтех-центр"
Составители: Пенкин М.А., Шувалов Н.Д.
E-mail: abitu@phystech.edu, fmicky@gmail.com
Сайт: www.abitu.ru