en.02

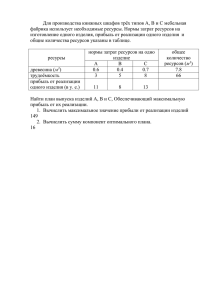
Пояснительная записка
Контрольно–оценочные средства (КОС) предназначены для контроля и
оценки образовательных достижений обучающихся, и освоивших программу
учебной дисциплины ЕН.02.Математика.
КОС включает контрольные материалы для проведения промежуточной
аттестации в форме зачета.
1.Общие положения
Требования к результатам освоения учебной дисциплины в соответствии с
ФГОС СПО:
Обучающийся должен уметь:
решать прикладные задачи в области профессиональной деятельности;
Обучающийся должен знать:
- значение математики в профессиональной деятельности и при освоении
ППССЗ;
- основные математические методы решения прикладных задач в области
профессиональной деятельности;
- основные понятия и методы теории вероятностей и математической
статистики;
- основы интегрального и дифференциального исчисления.
Уровень овладения умениями и знаниями в 1 семестре оценивается по
результатам текущего контроля знаний (среднее арифметическое).
Формой промежуточной аттестации по учебной дисциплине является зачет. Количество учебных часов ___2час. _ из_ _практических занятий.
2. Процедура проведения промежуточной аттестации
2.1 Условия выполнения заданий:
Зачет, который проводится на последнем практическом занятии, в виде
тестов, каждый из которых содержит 15 вопросов. Время выполнения работы
– 90 мин., количество вариантов – 3.
Задания составлены в соответствии с программой учебной дисциплины.
Процедура проведения зачѐта осуществляется в соответствии с положением о
промежуточной аттестации студентов КГБОУ СПО «Родинский медицинский
колледж».
3. Оценка освоения учебной дисциплины
3.1 Перечень вопросов для подготовки к зачету
1.
Предел функции в точке. Основные теоремы о пределах.
2. Предел функции при x, стремящемся к бесконечности. Замечательные
пределы. Число е.
3. Непрерывность функции в точке и на промежутке. Точка непрерывности
функции. Точка разрыва функции. Свойства непрерывных функций.
Приращение аргумента. Приращение функции.
4. Производная функции. Дифференциал функции. Геометрический смысл
производной. Механический смысл производной.
5. Таблица производных. Понятие сложной функции. Производная сложной
функции.
6. Схема исследования функции. Область определения функции. Множество
значений функции. Четность и нечетность функции. Нули функции.
Промежутки знакопостоянства функции. Возрастание и убывание функции,
правило нахождения промежутков монотонности. Точки экстремума
функции, правило нахождения экстремумов функции.
7. Производные высших порядков. Физический смысл второй производной.
Исследование функции с помощью второй производной.
8. Первообразная.
Неопределенный
интеграл.
Основные
свойства
неопределенного интеграла. Таблица неопределенных интегралов.
9. Методы интегрирования: метод непосредственного интегрирования; метод
замены переменной (метод подстановки); метод интегрирования по частям.
10.
Определенный интеграл. Понятие интегральной суммы. Достаточное
условие существования определенного интеграла (интегрируемости
функции).
11.
Основные свойства определенного интеграла. Геометрический смысл
определенного интеграла.
12.
Методы вычисления определенных интегралов. Формула НьютонаЛейбница.
13.
Геометрические и физические приложения определенного интеграла.
14.
Понятие дифференциального уравнения. Общее и частное решение
дифференциального уравнения. Линейные дифференциальные уравнения 1ого порядка. Задача Коши. Задачи, приводящие к дифференциальным
уравнениям.
15.
Методы решения дифференциальных уравнений.
16.
Основные понятия комбинаторики. Формулы перестановки, сочетания
и размещения элементов во множестве.
17.
Элементы и множества. Операции над множествами и их свойства.
18.
Графы. Элементы графов. Виды графов и операции над ними.
19.
Основные понятия теории вероятностей. Случайные события.
Классическое определение вероятности. Основные свойства вероятности.
20.
Основные теоремы и формулы теории вероятности. Формула
умножения теории вероятности. Формула сложения теории вероятности.
21.
Формула полной вероятности. Формула Бернулли.
22.
Случайные величины, законы их распределения и числовые
характеристики.
23.
Предмет математической статистики. Генеральная и выборочная
совокупности.
24.
Графические изображения выборки.
Полигон и гистограмма.
Выборочные характеристики.
25.
Понятие о медико-демографических показателях. Статистические
показатели для оценки деятельности поликлиники и стационара.
26.
Математические методы в профессиональной деятельности.
Практические задания для подготовки к зачету
5x
1.
7 

1  .
Вычислить предел lim

x 
 3x 
2.
Вычислить пределы:
5x 4  x 3  1
x3  2x
x2  4
;
б)
;
в)
.
lim
lim
x 
x  x 2  4
x  x 3  2 x
2x 4  x
sin 17 x
3.
Вычислить предел lim
.
x 0 sin 5 x
sin 5 x
4.
Вычислить предел lim
.
x 0
3x
а) lim
5.
6.
7.
8.
9.
3x 2  x
.
x 0 x 2  2 x
x 2  10 x  16
Вычислить предел lim
.
x8
x 8
5x
Исследовать функцию f ( x) 
на непрерывность в точке x0  6 .
x6
Вычислить предел lim
Исследовать функцию f ( x)  3x 2  x3 и построить ее график.
Вычислить значение производной следующих функций в точке x0  4 :
а) f ( x)  8x 2  ln x ; б) f ( x)  x 3  5x .
10.
Найти производную функции y  x 4  5x 2  x  .
11.
Найти производную функции y 
12.
Найти производную функции y  e 2 x 8 .
13.
7
11x  8
.
2x  4
5
Найти производную функции y  ln 8x 4  3x 2  2 .
Найти неопределенный интеграл
14.
4  x3  x 2  2x
dx .

x
Найти неопределенный интеграл методом замены переменной
2
x
 x  e dx .
15.
3
16.
Найти неопределенный интеграл методом замены переменной
 6 x  11 dx .
4
Найти неопределенный интеграл методом замены переменной
 cos(6 x  1)dx .
17.
Найти неопределенный интеграл методом замены переменной
6
 sin x  cos xdx .
18.
3
19.
Вычислить определенный интеграл  (5x  1)dx .
0
1
20.
Вычислить определенный интеграл  ( x  5) xdx .
0
2x3  x 4
Вычислить определенный интеграл 
dx .
x2
0
2
21.
22.
Скорость движения точки изменяется по закону v  5t 2  4t  2 (м/с).
Найти путь s, пройденный точкой за 4 с от начала движения.
23.
Вычислить объем тела, полученного от вращения фигуры,
ограниченной линиями y  x 2 , y  0 , x  1 , x  3 , вокруг оси Ox.
Вычислить площадь фигуры, ограниченной линиями y  x 2 , y  0 ,
x 1, x  2 .
25.
Решить дифференциальное уравнение y   9 y   20 y  0 .
26.
Решить уравнение A72  42 x
24.
27.
Вычислить C33  P3
28.
Вычислить
29.
Вычислить A104
32!
33!
30.
Тело движется прямолинейно со скоростью v  0,1t 3 м/с. Вычислить
путь, пройденный телом за 10 сек.
31.
Решить уравнение A52  20 x
32.
Решить дифференциальное уравнение y  11x .
33.
Вычислить площадь фигуры, ограниченной линиями
2
y=2x ; x=1 и x=2
34. Скорость движения точки изменяется по закону   3t 2  2t  1 м/с.
Найдите путь, пройденный точкой за 10 с от начала движения
35. В одной корзине находятся 5 белых и 10 черных шаров, в другой – 4
белых и 11 черных. Из каждой корзины вынули по шару. Найти вероятность
того, что оба шара окажутся черными.
36. В лотерее 1000 билетов. Разыгрывается один выигрыш в 200 рублей и
десять выигрышей по 100 рублей. Пусть Х – величина возможного выигрыша
для человека, имеющего один билет. Составить закон распределения этой
случайной величины Х.
37. Случайная величина Х задана законом распределения:
4
6
7
0,4
0,5
0,1
Найти математическое ожидание, дисперсию, среднее квадратичное
отклонение этой случайной величины Х.
Задания для оценки освоения
аттестации
Образец варианта задания:
дисциплины
при
промежуточной
Краевое государственное бюджетное образовательное учреждение среднего профессионального
образования «Родинский медицинский колледж»
Форма итоговой аттестации –зачет,
наименование учебной дисциплины - математика.
Рассмотрено
предметной Вариант 1
комиссией
Группа 15
«____» __________ 201___ г.
семестр 2
Председатель
Утверждаю
Зам. директора по УР
«____» ___________201__г.
Инструкция
Внимательно прочитайте задание. При выполнении заданий вы должны дать ответ с
полной записью решения, и только затем выбрать нужный вариант ответа. Вы
можете воспользоваться справочным материалом для выполнения задания.
Время выполнения задания 90 минут.
Задание 1
x 2  2x  6
Среди перечисленных вариантов ответа выбрать значение предела lim
x 3x 2  6 x  7
1
3
1
3) ;
3
1) - ;
2)  ;
4) 0.
Задание 2
sin 5x
:
x 0 2,5 x
Среди перечисленных вариантов ответов выбрать значение предела lim
1)   ;
Задание 3
2) 2;
3) 3;
4) 0.
2
В результате подстановки t  x  2 интеграл

xdx
2
(x  2) 5
приводится к виду …
1 dt
 5
2
t
1)
dt
2) 
t5
1 xdt
3)

2 t5
4)

xdt
t5
Задание 4
Производная функции у  х 5  е х имеет вид …
1) у /  5х 4  е х  х 5  е х ;
2) у /  5х 4  е х  х 5  е х ;
3) у /  5х 4  е х ;
4) у /  5х 4  е х .
Задание 5
Вторая производная функции y  
1
;
x4
3
3) y    4 ;
x
1) y   
1
равна:
x
2) y   
4) y  
6
;
x4
1
.
x4
Задание 6
Дифференциал функции у  8x 2  1 имеет вид …
1) 8xdx ;
2) dx ;
3) 16xdx ;
4) (2 x  1)dx .
Задание 7
В ящике 8 красных и 12 зеленых шаров. Из ящика случайным образом берут один
шар. Вероятность того, что этот шар окажется красным, равна …
1) 0,6%;
2) 1%;
3) 0,2%;
4) 0,4%.
Задание 8
Математическое ожидание дискретной случайной величины, заданной законом
распределения, равно …
Х
1
3
6
Р
0,2
0,3
0,5
1) 10;
2) 4,1;
3) 3,9;
4) 2.
Задание 9
Теория вероятности – это …
1) раздел математики, изучающий связи между вероятностями случайных событий;
2) раздел математики, изучающий связи между экспериментальными данными;
3) раздел математики, изучающий связи между методами систематизации;
4) раздел математики, изучающий связи между функциями.
Задание 10
Полигон – это …
1) график функции;
2) графическое изображение интервального ряда распределения;
3) графическое изображение дискретного ряда распределения;
4) графическое изображение отношения частоты к относительной частоте.
Задание 11
Преобразуйте 400 мг = ___г
1) 0,04;
2) 0,4;
3) 1,5;
4) 4
Задание 12
Для приготовления 1л 2% раствора хлорамина медсестра взяла 20 г хлорамина и __
мл воды.
1) 980
2) 990
3) 1 л
4) 560
Задание 13
В назначении указано: гидрокодон 10 мг в виде сиропа p.o. q.d. Имеются: сироп
гидрокодона 5 мл в котором содержит 5 мг гидрокодона битартрата. Больной
должен получить ___мл в день:
1) 1
2) 1,5
3) 5
4) 10
Задание 14
Множества, из n элементов по m элементов, которые отличаются друг от друга хотя
бы одним элементом, называются…..
1) перестановки
2) размещения
3) сочетания
4) соединения
Задание 15
Число объектов выборки или генеральных совокупности называют…
1)объектом выборки
2) размахом выборки
3)рядом
4)таблицей
Преподаватель____________________________
Краевое государственное бюджетное образовательное учреждение среднего
профессионального образования «Родинский медицинский колледж»
Форма итоговой аттестации – дифференцированный зачет,
наименование учебной дисциплины - математика.
Рассмотрено
предметной
комиссией
«____» __________ 201___ г.
Председатель
Вариант 2
Группа 15
семестр 2
Утверждаю
Зам. директора по УР
«____» ________201__г.
Инструкция
Внимательно прочитайте задание. При выполнении заданий вы должны дать
ответ с полной записью решения, и только затем выбрать нужный вариант ответа.
Вы можете воспользоваться справочным материалом для выполнения задания.
Время выполнения задания 90 минут.
Задание 1
x 3  2x  6
x 3x 2  6 x  7
Среди перечисленных вариантов ответа выбрать значение предела lim
1
3
1
3) ;
3
1) - ;
2)  ;
4) 0.
Задание 2
Среди перечисленных вариантов ответов выбрать значение предела lim
x 0
sin 6 x
:
sin 2 x
1)   ;
Задание 3
2) 2;
3) 3;
4) 0.
В результате подстановки t  x  4 интеграл
1)
2)
3)
4)
2
(
x

4
)
dx

приводится к виду …
t 3 dt
t 2 dt
1
2
1
2
t 2 dt
t 3 dt
Задание 4
Производная функции у  х 4  е х имеет вид …
1) у /  4х 3  е х  х 4  е х ;
2) у /  4х 3  е х  х 4  е х ;
3) у /  4х 3  е х ;
4) у /  4х 3  е х .
Задание 5
Вторая производная функции y  ( x  5) 2 равна…
1) y   2 ;
2) y   2 x ;
3) y   2 ;
4) y   10 .
Задание 6
Дифференциал функции у  x 5  1 имеет вид …
1) 5xdx ;
2) dx ;
4
3) 5 x dx ;
4) (5x 4  1)dx .
Задание 7
В ящике 2 белых и 8 черных шаров. Из ящика случайным образом берут один
шар. Вероятность того, что этот шар окажется белым, равна …
1) 1%;
2) 0,5%;
3) 0,2%;
4) 0,8%.
Задание 8
Математическое ожидание дискретной случайной величины, заданной законом
распределения, равно …
Х
4
5
6
Р
0,4
0,1
0,5
1) 15;
2) 5,1;
3) 4;
4) 6.
Задание 9
Основной вид статистической совокупности, называется …
1) общая
2) генеральная
3) репрезентативна
4) частная
Задание 10
Выборка – это …
1) множество объектов, случайно отобранных из генеральной совокупности;
2) множество объектов, однородных относительно нескольких признаков;
3) множество объектов, однородных относительно одного признака;
4) множество объектов, собранных по одному признаку.
Задание 11
Преобразуйте 500 мг = ___г
1) 0,05;
2) 0,5;
3) 2,5;
4) 5
Задание 12
50 г вещества растворены в 200 г воды. Концентрация раствора равна ___
1) 20%
2) 40%
3) 50%
4) 4%
Задание 13
В назначении указано: 200 мг гидрохлортиазида p.o. q.d. имеются таблетки
гидрохлортиазида по 50 мг. Больной должен получить ___таблеток внутрь один
раз в день:
1) 1/2
2) 1
3) 4
4) 3
Задание 14
Множества, из n различных элементов по m, которые отличаются составом или
порядком элементов, называются …
1) перестановки
2) размещения
3) сочетания
4) соединения
Задание 15
Событие, которое может либо произойти, либо не произойти называется…
1) достоверное
2) случайное
3) невозможное
4) невероятное
Преподаватель____________________________
Критерии оценки:

Оценка – 5 («отлично) ставится студентам, усвоившим взаимосвязь
основных понятий дисциплины, проявившим творческие способности в
понимании, изложении и использовании учебно –программного материала
(для выполнения письменной работы).

Оценка – 4 («хорошо») выставляется студенту, за хорошие знания,
показавшему систематический характер знаний по дисциплине к их
применению выполнения контрольной работы в ходе дальнейшей учебы.
Допускаются отдельные неточности..

Оценка - 3 («удовлетворительно») ставится студентам, обладающим
необходимыми знаниями, но допустившими неточности в определении
понятий, в применении знаний для решения практических заданий, не умет
обосновывать свои рассуждения, связывать теорию с реальностью.

Оценка - 2 («неудовлетворительно») ставится студентам, имеющим
разрозненные и бессистемные знания, не умеет выделять главное и
второстепенное, допускает неточности в определении понятий, искажает их
смысл, не может применять знания для решения практических задач (либо
за полное незнание и непонимание учебного материала).
Процент
результативности
(правильных ответов)
Качественная оценка уровня подготовки
балл (отметка)
вербальный аналог
90 ÷ 100
(14-15 заданий)
5
отлично
80 ÷ 89
(11-13 заданий)
4
хорошо
70 ÷ 79
( 9-10 заданий)
3
удовлетворительно
2
неудовлетворительно
менее 70
Эталоны ответов:
Вариант - 1
1. 3
2. 2
3. 1
4. 1
5. 2
6. 3
7. 4
8. 2
9. 1
10. 3
11. 2
12. 1
13. 4
14. 3
15. 1
Вариант -2
1. 4
2. 4
3. 1
4. 2
5. 4
6. 3
7. 2
8. 3
9. 3
10. 4
11. 3
12. 1
13. 4
14. 1
15. 2
Литература для студента:
 Дадаян А.А. Математика:Учебник-2-е издание.-М.:ФОРУМ:ИНФРАМ.2006.-552с.-(Профессиональное образование).
 Богомолов Н. В. Практические занятия по математике: Учебное пособие
для средних учебных заведений. / Н.В. Богомолов. – 7-е изд. М.:
Высшая школа, 2004.- 495 с.
 Гилярова, М.Г. Математика для мед.колледжей [Текст].- Ростов н/Д:
Феникс, 2011.- 410с.- (Медицина).- ISBN 978-5-222-17480-7
 Омельченко В.П.
Математика [Текст]: учеб.пособие / В.П.
Омельченко, Э.В. Курбатова.- 2-е изд. перераб. и доп.- Ростов н/Д:
Феникс, 2007.- 380с.- ( Среднее профессиональное образование).-ISBN
978-5-222-10441-5
 Омельченко, В.П. Математика. Компьютерные технологии в медицине
[Текст]: учебник / В.П. Омельченко, А.А. Демидова.- Ростов н/Д6
Феникс, 2008.- 588с.: ил. - ( Среднее профессиональное образование).ISBN 978-5-222-13022-3.
 Жохов, В.И. Алгебра [Текст]: Дидактические материалы / В.И. Жохов,
Ю.Н. Макарычев, Н.Г. Миндюк.- 6-е изд. – М.: Просвещение, 2001.144с.: ил.-ISBN 5-09-010487-5
 Макарычев, Ю.Н. Алгебра [Текст]: Дидактические материалы. – 5-е
изд.-М.: Просвещение, 2001.-160с.: ил..-ISBN 5-09-009614-7
 Математика [Текст]: Конспект первокурсника /сост. В.В. Барсуков. –
Мн.: Интерпрессервис,2002.- 22с.- ISBN 9-85-6656-92-3
Интернет ресурсы:
1. http://festival.1september.ru/
2. http://www.fepo.ru
3. www.mathematics.ru