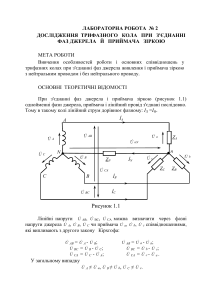
Диханов С.М., Цикало А.Л. Ф зична х м я. (Х м чна термодинам ка, Ф зико-х м чний анал з, К нетика). Навчальний пос бник
реклама

Міністерство освіти і науки України ОДЕСЬКА ДЕРЖАВНА АКАДЕМІЯ ХОЛОДУ Диханов С.М., Цикало А.Л. ФІЗИЧНА ХІМІЯ (Хімічна термодинаміка , Фізико-хімічний аналіз, Кінетика) Навчальний посібник Одеса 2010 1 Ди ха но в С .М . , Ц ика л о А.Л. Фізична хімія. (Хімічна термодинаміка , Фізико-хімічний аналіз, Кінетика). Навчальний посібник . Одеська державна академія хол оду, 2009. – 132 с. Посібник розроблено згідно з робочою навчальною програмою дисципліни «Фізична хімія» для студентів спеціальності 070801«Екологія та охорона навколишнього природного середовища» за напрямом підготовки 040106 «Екологія,охорона навколишнього середовища та збалансоване природокористування». Метою викладання дисципліни є формування у студентів теоретичних знань та практичних навичок у вивченні фізико – хімічних процесів які грають особливу роль і великою мірою визначають ефективність у функціонування очисного обладнання процеси адсорбції, абсорбції, фільтрування, виморожування, очищення та опріснення води, відстоювання та деемульгування сумішей тощо, приладів для якісного та кількісного визначення небезпечних домішок в атмосферному повітрі, воді, ґрунтах, харчових продуктах і т.п. Наведені зразки тестових питань для поглибленого опрацювання з посиланнями на літературу, яка є в бібліотеці ОДАХ. Рецензент: професор, д.х.н. Андріанов А.М. Завідувач кафедри хімії, охорони раціонального природокористування, проф. навколишнього середовища і /А.Л.Цикало/ Голова науково-методичної комісії напряму підготовки Екологія,охорона навколишнього середовища та збалансоване природокористування, проф. /А.Л.Цикало/ 2 ЗМІСТ ВСТУП ................................................................................................................ 5 РОЗДІЛ 1. ХІМІЧНА ТЕРМОДИНАМІКА ................................................... 8 1.1. Основні поняття термодинаміки ................................................................ 9 1.2. Перший закон термодинаміки .................................................................. 12 1.2.1. Робота і теплота у термодинамічних процесах .................................... 14 1.3. Термохімія.................................................................................................. 16 1.3.1. Закон Гесса .............................................................................................. 17 1.3.2. Теплоємність ........................................................................................... 19 1.4. Залежність внутрішньої енергії та ентальпії від температури .............. 23 1.5. Залежність теплового ефекту реакції від температури .......................... 24 1.6. Другий закон термодинаміки ................................................................... 26 1.6.1. Математичний вираз другого закону термодинаміки ......................... 27 1.6.2. Ентропія та ймовірність ......................................................................... 30 1.6.3. Статистичний характер другого закону термодинаміки ..................... 32 1.6.4. Зміна енергії в різних процесах ............................................................ 32 1.6.5. Термодинамічні потенціали .................................................................. 34 1.6.6. Характеристичні функції ....................................................................... 36 1.6.7. Термодинаміка хімічних реакцій .......................................................... 37 1.6.8. Розрахунки термодинамічних потенціалів ........................................... 40 1.7. Хімічний потенціал ................................................................................... 42 1.8. Хімічна рівновага ...................................................................................... 45 1.8.1. Рівновага в гетерогенних системах ....................................................... 48 1.8.2. Напрямок фізико-хімічних перетворень у гетерогенних системах ... 49 1.8.3. Рівняння ізотерми хімічної реакції ....................................................... 50 1.8.4. Залежність хімічної рівноваги від температури .................................. 51 1.9. Третій закон термодинаміки ..................................................................... 53 Контрольні запитання ...................................................................................... 56 2. ФІЗИКО-ХІМІЧНИЙ АНАЛІЗ .................................................................... 60 2.1. Застосування другого закону термодинаміки до фазових перетворень 60 2.2. Загальні умови рівноваги в гетерогенних системах. Правило фаз Гіббса ............................................................................................................................ 62 2.3. Фазові рівноваги в однокомпонентних ................................................... 64 2.3.1. Рівняння Клаузіуса-Клайперона ........................................................... 64 2.3.2. Діаграми стану води та сірки ................................................................ 66 2.3.3. Характеристика поліморфних перетворень. Діаграма стану фосфору ............................................................................................................................ 70 2.4. Фазові рівноваги у двокомпонентних системах ..................................... 73 2.4.1. Основи фізико-хімічного аналізу .......................................................... 73 2.4.2. Діаграми стану двокомпонентних систем з евтектикою .................... 76 2.4.3. Діаграми стану двокомпонентних систем,в яких утворюються конгруентно та інконгруентно плавкі хімічні сполуки ................................. 80 3 2.4.4. Діаграми стану двокомпонентних систем, у яких співіснують фази змінного складу ................................................................................................ 84 2.4.5. Тверді розчини та їх класифікація ........................................................ 85 Контрольні запитання ...................................................................................... 87 Розділ 3.ХІМІЧНА КІНЕТИКА І КАТАЛІЗ .................................................. 88 3.1. Швидкість хімічної реакції ....................................................................... 88 3.2. Класифікація хімічних реакцій ................................................................ 92 3.3. Кінетика односторонніх простих реакцій ............................................... 92 3.4. Способи визначення порядку реакції ...................................................... 94 3.5. Кінетика складних реакцій ....................................................................... 95 3.6. Теоретичні уявлення хімічної кінетики................................................... 98 3.6.1. Теорія активного комплексу або перехідного стану ........................... 99 3.6.2. Теорія активних зіткнень ..................................................................... 100 3.7. Ланцюгові реакції .................................................................................... 102 3.8. Кінетика гетерогенних процесів ............................................................ 104 3.9. Каталіз ...................................................................................................... 105 3.10. Гомогенний каталіз ............................................................................... 108 3.11. Ферментативний каталіз ....................................................................... 109 3.12. Гетерогенний каталіз............................................................................. 113 Контрольні запитання .................................................................................... 117 ТЛУМАЧНИЙ СЛОВНИК ............................................................................ 120 Література ....................................................................................................... 126 Додаток: Зразок тесту .................................................................................... 127 4 ВСТУП Курс фізичної хімії в загальній системі підготовки майбутніх фахівців – екологів займає особливе місце. Річ у тому, що саме фізико – хімічні процеси грають особливу роль і великою мірою визначають ефективність у функціонування очисного обладнання процеси адсорбції, абсорбції, фільтрування, виморожування, очищення та опріснення води, відстоювання та деемульгування сумішей тощо, приладів для якісного та кількісного визначення небезпечних домішок в атмосферному повітрі, воді, ґрунтах, харчових продуктах і т.п. Значення курсу фізичної хімії полягає також у тому, що цей курс створює своєрідний міст між екологічними задачами і відповідними науковими принципами та інженерним, апаратурним оформленням відповідного обладнання, апаратів, приладів, технічних конструкцій. Зрозуміло, що рішення цієї проблеми потребує не тільки знання принципів та положень фізичної хімії, але й відповідних практичних навичок виконання необхідних розрахунків, технічних розробок, інженерних креслень (у тому числі, з використанням сучасної комп’ютерної техніки). Зрозуміло що володіння положеннями фізичної хімії важливе не тільки власне для професійної підготовки майбутніх фахівців – екологів, але й в більш широкому сенсі – для розширення наукового і технічного кругозору студентів, підвищення загального рівня їхньої екологічної культури. Це має сприяти вирішенню важливої проблеми природоохоронної справи щодо поліпшення екологічного становища довкілля, очищення повітря, підвищення якості питної води, ґрунтів, харчових продуктів. Курс фізичної хімії грає також неабияку роль в індивідуальній роботі з талановитими студентами підготовка студентських наукових публікацій, та доповідей на обласні, всеукраїнські та міжнародні наукові конференції, конкурсних студентських наукових робіт, підготовка студентів до участі в першому та другому турах Всеукраїнських олімпіад з хімії, екології, безпеки життєдіяльності. Поняття фізична хімія виникло ще в XVII ст., а отримало розповсюдження тільки в XVIII ст. В першій половині XVIII ст. з'явився порадник за назвою «Фізична хімія», в якому наводилися фізико-хімічні описи явищ, що відбувалися навколо нас. Хімія сприймалася як мистецтво розділяти речовини на складові частини (аналіз) та складати тіла з них 5 джерел (синтез). Але все це не мало жодного стосунку до науки. Основне завдання вчених на той час було перетворити хімію з мистецтва на науку. Затвердженню ідеалу фізики, яка вже тоді була самостійною наукою завдяки роботам Ісаака Ньютона, в хімії помітно сприяли роботи М.В. Ломоносова, котрий наголошував на перспективі корисного взаємозв'язку хімії та фізики: «Обидві науки, — стверджував він, — завдяки взаємній допомозі отримують потужний розвиток, оскільки легше розпізнати приховану природу тіл, якщо ми з'єднаємо фізичні істини з хімічними». М.В. Ломоносову належить перша програма фізико-хімічних досліджень. Центральне місце в пій підводиться кількісним вимірюванням: «Перевірити все, що тільки можна вимірювати, зважувати та визначати обчисленнями». Щоб зрозуміти це висловлення вченого, варто звернути увагу на те що раніше всі хіміко - аналітичні описи явищ зводилися до якісного аналізу. Тобто стверджували, що дана речовина твердіша або м’якша, ніж інша, довша, чи ширша. Невміння кількісно описати те чи інше явище приводило хіміків до невірних висновків, внаслідок чого неможливо було встановити якісь закономірності в хімії. Наприклад, вага речовин вважалася за їх якість і, як і будь-яка якість, вона повинна була залежати під температури, тиску та інших факторій. Якісно це підтверджувалося і в дослідах, оскільки нагрівання деяких матеріалів спричиняло або зменшення їхньої ваги (за рахунок десорбції газів, наприклад), або підвищення (за рахунок окислення). Тому стає зрозумілим, чому всі досліди М.В. Ломоносова в 1752— 1756 роках були спрямовані на «вимірювання міри, ваги та їх пропорцій». Мине багато часу і Д.І. Менделєєв скаже: «У природі міра та вага — головна зброя пізнання». Таким чином, роботи М.В. Ломоносова та паралельно англійського вченого Дж. Блока стверджували основоположний принцип збереження маси речовин в хімічних реакціях. Тоді ж була висловлена думка, що атоми речовин мають досить визначену масу. Це дало можливість Дж. Дальтону в 1803 р. відкрити один з найважливіших законі» хімії — закон простих кратних відношень, який за допомогою уявлень про атоми дозволив пояснити причину певних відношень елементів у хімічних сполуках. Таким шляхом сформувалося атомне вчення — хімічна атомістика, яка визначила розвиток хімії до панюго часу. 6 В подальшому (XIX—XX ст.) фізична хімія працями Д.У. Гіббса. Д.І. Менделєєва, Вант-Гоффа, В.Ф. Оствальда, Св. Арреніуса, А.Л. Ле Шательє, В. Нернста та ін. сформувалася в гак звану класичну фізичну хімію, яка включала в себе: термохімію, електрохімію, фазові рівноваги, вчення про розчини та хімічну кінетику. Оновлення класичної фізичної хімії відбулося на початку XX ст. Особливо відчувалася в ній на ту нору нестача чіткої та фізично обґрунтованої теорії будови атомів і хімічного зв'язку. Все це вона потім отримала від фізики, яка створила квантову теорію будови атому та утворення хімічного зв'язку. Сучасна фізична хімія включає в себе також вчення про будову атомів та молекул, природу хімічного зв'язку і хімічну кінетику. Фізична хімія — це самостійна наука, що вивчає взаємозв'язок фізичних та хімічних явищ. Головне завдання фізичної хімії — передбачити проходження хімічного процесу в часі та кінцевий результат (стан рівноваги) за різних умов па основі даних про будову і властивості молекул речовин, що створюють систему. Іншими словами, фізична хімія — це наука, яка використовує закони фізики для пояснення хімічних явищ. Термін «фізична хімія» та визначення цієї науки, як уже зазначалось, були вперше запропоновані М.В. Ломоносовим в 1752—1754 роках: «Фізична хімія — це наука, яка па основі положень та дослідів фізики пояснює, те, що відбувається у змішаних тілах при хімічних реакціях». Визнання фізичної хімії як самостійної науки та навчальної дисципліни відбулося в затвердженні в Лейпцігському університеті 1887 р. першої кафедри фізичної хімії на чолі з видатним хіміком В.М. Оствальдом. Розрізняють фізичну та хімічну форму руху матерії. Для хімічної, тобто хімічного процесу, характерна зміна числа та розташування атомів у молекулах речовин, що реагують між собою. А це, в свою чергу, залежить від фізичної форми руху — коливання атомів та молекул. Фізична хімія поділяється па класичну та сучасну. Класична фізична хімія складається з наступних розділів: 1. Хімічна термодинаміка, що вивчає фундаментальні співвідношення, які ґрунтуються па І та II законах термодинаміки. Ці співвідношення дозволяють: розрахувати кількість тепла, що поглинається або виділяється в будь-якому процесі; визначити можливість самовільного проходження процесу в бажаному напрямку; визначити умови рівноваги та 7 напрямок зміщення процесу при зміні зовнішніх умов. 2. Термодинаміка розчинів, яка вивчає їх природу, внутрішню структуру та найважливіші пласти пості. Останні розглядаються у функціональній залежності від концентрації та хімічної природи компонентів. 3. Фізико-хімічний аналіз гетерогенних систем, де розглядаються питання фазових рівноваг одно-, дво-, трикомпонентних систем, їх фазові діаграми та методи їх дослідження. 4. Електрохімія, яка вивчає взаємозв'язок між перетвореннями хімічної енергії па електричну, властивості розчинів електролітів, їх електропровідність, явище електролізу, роботу гальванічних елементів та електрохімічну корозію металів. 5. Хімічна кінетика і каталіз — це визначення швидкостей та механізму хімічних реакцій, а також явища каталізу. У сучасній фізичній хімії додаються розділи про будову речовини, де вивчається зв'язок між будовою атомів та молекул і їх фізичними та хімічними властивостями, та фотохімія — наука про хімічці реакції під дією світла. Як визначив видатний сучасний фізико-хімік Н.М. Еммануель, є три головні складові хімії панюго часу: хімічна статика, що вивчає склад та будову речовин, хімічна динаміка, яка має справу з механізмами і законами перетворень речовин, та, нарешті, хімічні явища, відкриття та використання яких багато в чому визначають успіхи сучасного науково-технічного прогресу (високотемпературна надпровідність, напівпровідникова техніка, термоядерний синтез тощо). РОЗДІЛ 1. ХІМІЧНА ТЕРМОДИНАМІКА Термодинаміка вивчає закони взаємних перетворень різких видів енергії, стану рівноваги та їх залежність від різних факторів, можливість та межу перебігу самовільних процесів. Залежно від поставлених завдань розрізняють фізичну (загальну), технічну, хімічну та біохімічну термодинаміку. В загальній термодинаміці розглядаються основні закони (начала) термодинаміки та їх наслідки. Технічна термодинаміка вивчає застосування основних законів та їх наслідків до теплових двигунів. Хімічна термодинаміка, як випливає з 8 самої назви, с науковою дисципліною, що використовує математичний апарат та положення класичної термодинаміки для опису закономірностей перебігу хімічних реакцій та фазових переходів. Перетворення хімічної або інших форм енергії в живих організмах є предметом вивчення біохімічної термодинаміки. Вихідними положеннями термодинаміки с основні начала або закони, що не доводяться логічно, а підтверджуються чисельними дослідними даними. Вірність цих законів базується па основі багатовікового досвіду і в практичній діяльності не спостерігається явищ, які б їм суперечили. Хімічна термодинаміка оперує статистичним методом. В його основі покладено точку зору, що властивості тіл залежать від властивостей часток і характеру їх руху. Статистична термодинаміка широко використовує метод теорії ймовірності. Методами статистичної термодинаміки обґрунтовується друге та третє начала термодинаміки. Особливістю термодинамічного методу є його використання тільки до систем, що складаються з великої кількості окремих часток. Предметом вивчення хімічної термодинаміки є: — переходи енергії з однієї форми в іншу, від однієї частини системи до іншої; — енергетичні ефекти, що супроводжують різні фізичні або хімічні процеси, залежність їх від умов протікання процесів; — визначення можливості, напрямків та межі протікання самих процесів в розглянутих умовах. Хімічна термодинаміка включає вчення про теплові ефекти, розчини, хімічну рівновагу, фазові переходи та процеси на межі розділу фаз. 1.1. Основні поняття термодинаміки Основними поняттями та величинами термодинаміки є система та її властивості, фаза, стан системи, параметри етапу системи, термодинамічний процес. У хімічній термодинаміці вивчають системи, що складаються з дуже великої кількості часток. До окремих молекул, атомів або елементарних 9 часток вона не застосовується. Термодинамічною системою називають будь-яке тіло або сукупність тіл, що знаходяться у взаємодії і фактично або уявно виділені з навколишнього середовища. Вони здатні обмінюватися між собою та з іншими тілами енергією й речовиною. В хімічній термодинаміці розглядають такі типи систем: ізольована — це система, що не обмінюється речовиною та енергією з навколишнім середовищем і має сталий об'єм (V = соnst); закрита — це система, яка не обмінюється речовиною, але обмінюється енергією, маса такої системи постійна; відкрита — реакційна система, яка обмінюється з навколишнім середовищем масою та енергією, тобто з якої безперервно відводяться продукти реакції і підводяться вихідні речовини. Основними в термодинаміці є ізольована та закрита системи. Тільки в них досягається стан повної термодинамічної рівноваги. Ці системи зберігаються самі собою і з часом переходять в найбільш стійкій стан, з якого вони самовільно вийти не можуть. Прикладом ізольованої системи є замкнутий реакційний сосуд з теплоізоляційними стінками; зачинена кімната лабораторії або цеху, де відбуваються різні процеси; земна куля з навколишньою атмосферою тощо. Всередині ізольованої системи знаходяться окремі системи і оточуюче їх середовище, між якими відбувається обмін енергією або масою. Ідеально ізольовані системи с науковою абстракцією, до яких більшою або меншою мірою наближаються реальні тіла. їх взаємодією з іншими системами можна знехтувати. З практичної точки зору найбільш важливі закриті системи. Прикладом може бути герметичний реакційний сосуд з теплоізоляційними стійками або циліндр з добре пригнаним поршнем, в якому знаходиться досліджувана речовина. Термодинаміка відкритих систем почала бурхливо розвиватися завдяки термодинамічним дослідженням біологічних систем. До відкритих систем належать всі живі істоти, шматок іржавого заліза, гнилого дерева, посудина з кип'яченою водою. Якщо у системі властивості всіх її ділянок однакові, то система є однорідного. Відсутність поверхні розділу між частинками є ознакою 10 гомогенної системи. Система, що складається із різних за властивостями частин, розмежованих поверхнею розділу, тобто має дві або більше фаз, є гетерогенною Під фазою розуміють сукупність усіх однорідних частин системи, що маю однакові властивості і відокремлені від інших частин системи поверхнею поділу. Стан термодинамічної системи характеризується сукупністю термодинамічних параметрів. Фізичні величини, що характеризують стан системи, піддаються безпосередньому виміру і не залежать від способу досягнення даного стану, називають параметрами стану. Основними параметрами є об'єм V, тиск Р, температура Т та концентрація. Зміна стану системи за часом — термодинамічний процес. Процеси, що розглядаються в термодинаміці, поділяються на термодинамічно зворотні, які можна здійснити як в прямому, так і зворотному напрямках через ті ж самі стадії, та незворотні, для яких такі переходи неможливі. Якщо в системі відбулися зміни, які повернули її у початкове положення, то система здійснила коловий процес або цикл. Залежно від того, які параметри під час переходу системи з одного стану в інший залишаються сталими, процеси поділяють на ізохорні (V=const), ізобарні (Р = const), ізотермічні (Т = const) та адіабатні (G=const). Адіабатний процес відбувається без теплового обміну з навколишнім середовищем. Серед різних величин, що характеризують систему, особливе місце належить функціям, зміна яких визначається тільки початковим і кінцевим станом системи і не залежить від шляху протікання процесу їх називають функціями стану системи. Простішою функцією стану є об'єм системи, зміна якого не залежить від шляху процесу і визначається його початковим (V1) і кінцевим (V2) значеннями: V = V2 — V1. Якщо відбувається циклічний процес, то кінцевий стан збігається з початковим і будь-який параметр етапу приймає початкове значення, а його зміна перетвориться на нуль. Математична зміна параметра V в процесі — це сума його малих змін на 2 окремих ділянках процесу, і тоді V dV або 1 2 dV 0 тобто це 1 нескінченно мала зміна параметрів, що визначає величину повного диференціалу. Більш важливим з термодинамічної точки зору с поняття про 11 внутрішню енергію системи (U). Вона характеризує повний запас енергії системи і складається із суми кінетичної, потенціальної, поверхневої, магнітної енергій руху молекул, атомів, ядер та електронів у молекулах і атомах, внутрішньоядерної енергії, енергії міжатомної та міжмолекулярної взаємодії тощо. Абсолютне значення внутрішньої енергії виміряти неможливо, але можна визначити її зміну: U U 2 U1 Зміна внутрішньої енергії системи U під час будь-якого процесу не залежить від того, як він відбувається, а залежить від початкового та кінцевого станів системи. Внутрішня енергія — це функція стану системи, тобто повний диференціал від змінних температури та об'єму: dU (U / T )v dT (U T )T dV (1.1) 1.2. Перший закон термодинаміки Перший закон термодинаміки є емпіричним, абсолютно точним законом природи. Він має багато визначень, взаємопов'язаних між собою: — Енергія ізольованої системи постійна. — Різні форми енергії перетворюються одна в іншу при постійних еквівалентних співвідношеннях. — Неможливо створити «вічний двигун першого роду», тобто машину, що створює роботу без затрати енергії. Теплота (Q), одержана із зовнішнього середовища, перетворюється в роботу (А), створену системою, і викликає приріст внутрішньої енергії системи U . Вищенаведене твердження може бути записане в математичній формі Q=А+ U (1.2) Рівняння (1.2) є аналітичним виразом першого початку термодинаміки, що дозволяє розрахувати будь-яке перетворення енергії. Перший закон термодинаміки є наслідком закону збереження енергії, що дозволяє характеризувати різні види енергії еквівалентними величинами. Закон збереження і перетворення енергії порівнюється з філософським поняттям про нескінченний рух. Форми руху матерії змінюються. Залежно від характеру руху частої:, що беруть участь в передачі енергії, існують дні форми її передачі. Якщо енергія передається шляхом хаотичного 12 зіткнення частинок, то формою передачі енергії є теплота, якщо ж шляхом упорядкованого руху частинок під дією зовнішньої сили, то виконується робота. Теплота та робота характеризують якісно і кількісно дві різні форми передачі енергії від одного тіла до іншого. На підміну від внутрішньої енергії теплота і робота не є функціями стану. Це різні форми передачі енергії. Через це теплоту та роботу можна віднести лише до процесу, а не до стану. Теплоту, підведену до системи, беруть зі знаком «плюс», а теплоту, передану від системи в навколишнє середовище, — зі знаком «мінус». Перший закон термодинаміки встановлює співвідношення між теплотою Q і роботою А при зміні загального запасу енергії системи: U Q A (1.3) У будь-якому процесі збільшення внутрішньої енергії певної системи ΔU дорівнює різниці теплоти Q, наданій цій системі і кількості роботи А, яку виконала система. Для будь-якого елементарного процесу рівняння (1.3) має вигляд: dU Q A (1.4) Оскільки Q і A не є функціями стану, нескінченно малий їх приріст не буде повним диференціалом. Такий приріст позначається символом . Не слід вважати, що тепловий ефект хімічної реакції та робота розширення ідеального газу за певних умов є функціями стану. Для зворотного процесу вираз (1 3) має вигляд: 2 та для ізольованого процесу (dA 0; dQ 0) dV 0, 1 тобто U=const, U 0 (1.5) внутрішня енергія постійна. На основі вищевикладеного можна дати ще одне визначення першого закону термодинаміки: «Внутрішня енергія системи — це однозначна, кінцева і безповоротна функція стану системи». Якби цей висновок був невірний і енергія системи могла би збільшуватися без взаємодії 13 з навколишнім середовищем, то можна було б створити вічний двигун першого роду. Усі визначення першого закону термодинаміки відображають незнищеність і еквівалентність енергії при переході різних її видів один в інший. Визначення першого закону термодинаміки залежать від того, яка система розглядається. Теплота, підведена до закритої системи, витрачається на збільшення її внутрішньої енергії та на виконання системою роботи проти зовнішніх сил. У відкритих системах крім обміну енергією з оточуючим середовищем змінюється склад системи і її маса. Залежно від того, які параметри системи будуть сталими, перший закон термодинаміки матиме різний вигляд. Якщо об'єктом дослідження є ідеальний газ, то при сталій температурі зміна внутрішньої енергії дорівнює нулю (закон Джоуля). Уся теплота переходить у роботу: dQ = dA.. Оскільки dA = PdV, a РV = RТ, то A v2 RTdV / V RT ln V2 / V1 (1.6) v1 При ізохорному процесі відсутня робота розширення (V = сопst; dА = РdУ = 0 ) . Теплота, що підведена до системи, витрачається па збільшення внутрішньої енергії системи dU = dQ. Тобто QV=ΔU (1.7) теплота при ізохорному процесі є функцією етапу. При розгляді першого закону термодинаміки в ізобарному процесі введемо нову функцію H = U + РV яка називається ентальпією. Її диференціал dH = dU+PdV+VdP = dQ+VdP. Звідси при сталому тиску зміна ентальпії дорівнює теплоті при сталому тиску: QP=ΔH (1.8) — Оскільки ентальпія, як і внутрішня енергія, є функцією стану, теплота в ізобарному процесі є також функцією етапу. 1.2.1. Робота і теплота у термодинамічних процесах Якщо під час реакції збільшується об'єм dV а зовнішній тиск дорівнює Р. то викопується робота розширення 14 (1.9) або Інтегрування можливе для процесії:, що наближаються до рівноважних. Результат його залежатиме під умов, за яких проходить процес. Переважна більшість хімічних процесів відбувається при сталому (атмосферному) тиску. Для ізобарного процесу робота розширення (1.10) Для ідеального газу PV = nRT. Тоді (1.11) Для ізотермічного процесу (1.12) Після інтегрування цього виразу (1.13) Якщо T = const, то P1V2 = P2V1, тому (1.14) При адіабатному процесі газ не отримує теплоти зовні і не віддає, тобто Q =0. Робота викопується за рахунок зменшення внутрішньої енергії. Газ охолоджується: A = -ΔU (1.15) При ізохорному процесі (V = соnst) робота розширення не виконується A = 0. 15 1.3. Термохімія При хімічних реакціях має місце зміна внутрішньої енергії системи, оскільки внутрішня енергія продуктів реакції відрізняється під внутрішньої енергії вихідних речовин. Це відбувається за рахунок виділення (або поглинання) теплоти і виконання роботи. Розділ хімічної термодинаміки, що вивчає теплові ефекти хімічних реакцій, фазових перетворень та інших фізико-хімічних процесів, називають термохімією. Термохімічні дані мають велике значення для теорії різних технологічних процесів, утому числі й для технологій виробництва харчових продуктів та напоїв, при розрахунку автоклавів тощо. Термохімічні величини необхідні для обчислення найважливіших характеристик реакцій: термодинамічного потенціалу та константи рівноваги. Теоретичні закономірності термохімії — це наслідок першого закону термодинаміки. У термохімічних розрахунках користуються головним чином величинами теплових ефектів хімічних реакцій та фізико-хімічних процесів. Тепловим ефектом хімічної реакції або будь-якого фізико-хімічного процесу називається зміна внутрішньої енергії (при V = соnst). або ентальпії (при Р = сonst) при однаковій температурі початкових і кінцевих продуктів. Теплові ефекти визначають як експериментально, так і за допомогою термохімічних розрахунків. Залежно від умов перебігу хімічної реакції досягатимуться різні теплові ефекти QV або QP. Зміна об'єму під час хімічної реакції зумовлена появою або зникненням газоподібних речовин. Якщо гази не беруть участі в реакції, то зміна об'єму, а також робота розширення с незначними і ними можна знехтувати. Застосовуючи до газоподібних речовин, що беруть участь у реакції, закони ідеальних газів при Т = сonst можна записати (1.16) Тоді (1.17) Δn — зміна кількості молів газоподібних речовин. Якщо гази не беруть участі в реакції, практично Δn= 0 і QP. = QV. де 16 1.3.1. Закон Гесса Основним законом термохімії є закон, сформульований в 1840 році академіком Російської академії наук Г.І. Гессом. Встановлений дослідним шляхом ще до відкриття першого закону термодинаміки, цей закон стверджує, що тепловий ефект хімічної реакції залежить від початкового і кінцевого етапу речовин, що беруть участь у реакції, і не залежить від проміжних стадій, шляху процесу та механізму реакцій. Тобто. якщо із початкових речовин можна одержати задані кіпцеві продукти різними шляхами, то сумарний тепловий ефект па одному шляху дорівнює сумарному тепловому ефекту процесу на будь-якому іншому шляху. Закон Гесса є наслідком першого закону термодинаміки, коли теплота є функцією стану. Цей закон широко використовують у різних термохімічних розрахунках. Він дає можливість визначити теплові ефекти процесів, для яких експериментальні дані відсутні. Особливо тоді, коли неможливо провести експеримент, або для нових процесів, які ще не відбувалися. Закон Гесса застосовують як до хімічних реакцій, так і до фізико-хімічних процесів розчинення, випаровування, кристалізації, адсорбції. Температура вихідних речовин і продуктів реакції має бути однаковою. Хімічні рівняння, в яких поряд зі стехіометричними коефіцієнтами та формулами речовин є дані про теплові ефекти, називають термохімічними. Оперують ними як звичайними алгебраїчними рівняннями. При цьому теплові ефекти реакції залежать від агрегатного стану та кристалічної модифікації реагуючих речовин. Тому в термохімічних рівняннях приводять агрегатний етап речовин. Теплові ефекти реакцій залежать і від параметрів етапу реагуючих речовий, наприклад температури. В термохімічних розрахунках використовують теплові ефекти за стандартних умов: при тиску 101,3 кПа і температурі 298К. Закон Гесса мас такі наслідки: — Теплота реакції утворення складних сполук із простих речовин дорівнює теплоті утворення цієї сполуки. Теплота утворення простих речовий за стандартних умов дорівнює нулю. Теплота утворення — це кількість теплоти, що виділяється або поглинається при утворенні одного моля речовини з простих речовин. Із самого визначення випливає, що теплота утворення є окремим випадком теплового ефекту хімічної реакції, коли як вихідні продукти беруть прості речовини, стійкі за певних умов. 17 Наприклад: Са + 1/20 2 = СаО; H 0f 298 = - 631 кДж/моль. Стандартну теплоту утворення речовин позначають H 0f 298 . Для великої кількості речовин значення стандартних теплот утворення визначені і наведені в термодинамічних довідниках. — Теплові ефекти можна визначити за теплотою утворення або теплотою згоряння. Якщо реагують неорганічні сполуки, то тепловий ефект хімічної реакції дорівнює різниці суми теплот утворення продуктів реакції і суми теплот вихідних речовин з урахуванням стехіометричних коефіцієнтів перед формулами цих речовин рівнянні реакції. Для реакції типу: aA + bB = cC + dD де A, В — відповідно вихідні речовини; С, D— продукти реакції; а, b, с, d — стехіометричні коефіцієнти; тепловий ефект реакції за стандартних умовах дорівнює: Якщо в хімічній реакції беруть участь органічні сполуки, то тепловий ефект дорівнює: сумі теплот згорання вихідних речовин мінус сума теплот згорання кінцевих продуктів реакції. Теплота згорання — це кількість теплоти, що виділяється під час згорання 1 моль речовини до утворення вищих оксидів. Теплота згорання харчових продуктів у живому організмі с джерелом енергії, за рахунок якої здійснюється його життєдіяльність. За теплотою згорання розраховують калорійність харчових продуктів. Наприклад, теплота згорання вуглеводів H зг0 =17,1 кДж/г, жирів H зг0 = 38,9 кДж/г, білків H зг0 = 17,1 кДж/г. Теплові ефекти прямої і зворотної реакції рівні за алгебраїчними величинами, але протилежні за знаком. Якщо в двох реакціях початкові стани різні, а кінцеві — однакові, 18 то різниця теплових ефектів цих реакцій дорівнює тепловому ефекту переходу з одного початкового етапу в інший. Наприклад; Тепловий ефект переходу графіту в алмаз H зг H10 H 20 Якщо в двох реакціях початкові етапи однакові, а кіпцеві різні, то різниця теплових ефектів цих реакції дорівнює тепловому ефекту переходу з одного стану в інший. Наприклад: Тепловий ефект переходу водяної пари в рідину H 0 H10 H 20 Розчинення речовин супроводжується як виділенням, так і поглинанням теплоти, що залежить від хімічної природи розчинених речовин і розчинника. Теплота розчинення — це кількість тепла, що виділяється або поглинається при розчиненні одного моля речовини з утворенням розчину заданої концентрації. Теплота розчинення 1 моля речовими в (n) молях розчинника є інтегральною теплотою розчинення. Наближено теплоту розчинення можна записати у вигляді двох додатків: H H1 H 2 де H1 — теплота переходу речовини, що розчиняється, в той стан, в якому вона існує в розчині; H 2 — теплота сольватації, яка завжди має від'ємне значення. Для газів H1 < 0, для твердих тіл H 2 > 0. Величина H 2 розраховується з різниці значень теплоти розчинення і енергії кристалічної решітки; H 2 H1 H 1.3.2. Теплоємність Однією із найважливіших теплових характеристик речовин та процесів у екосистемах є теплоємність. Теплоємність системи дорівнює 19 кількості теплоти, яку необхідно підвести або віднести від цієї системи для зміни її температури на один градус. Теплоємність системи має адитивні властивості. Для системи з і-елемептів вона дорівнює сумі теплоємностей цих елементів: C Ci де Сі — теплоємність і-го компонента системи. Цю залежність використовують не тільки для розрахунків теплоємностей сплаві і сполук, а й деяких харчових продуктів Відрізняють істинну, середню, питому, молярну та об'ємну теплоємність. Середня теплоємність системи дорівнює кількості теплоти, що необхідно передати цій системі для нагрівання її па один градус в умовах відсутності корисної роботи: C Q /(T2 T1 ) (1.18) де Q — кількість теплоти, надана системі; T1 , Т2 — відповідно початкова та кінцева температура системи. Теплоємність одного кілограму речовини називають питомою теплоємністю (Дж/(кгК)) Cnum Q /(mT ) де (1.19) m — маса речовини, кг; T — зміна температури; Теплоємність 1 моля речовини — молярною Дж/(моль*К) CM Q /(nT ) (1.20) За законом Коппа-Неймана молярна теплоємність твердих сполук дорівнює сумі атомних теплоємностей простих речовин: Ci ni Ci де ni — число атомів; Сi — атомна теплоємність елемента. Теплоємність 1 м 3 речовини є об'ємною теплоємністю (Дж/м 3 *К) Cоб Q /(V T ) де (1.21) V — об'єм, що займає речовина. Величина Q / dT C 20 (1.22) називається істинною теплоємністю і виражає нескінченно малу кількість теплоти, що підвели до системи для підвищення температури на нескінченно малу величину dТ. Теплоємність системи залежить від умов передачі (відняття) теплоти. Якщо система знаходиться ари сталому об'ємі, то згідно з першим законом термодинаміки, вся теплота використовується на збільшення запасу внутрішньої енергії QV U . Поділивши прану та ліву частини цього рівняння на T отримаємо: (1.23) При сталому тиску частина теплоти спрямовується на виконання роботи розширення протії зовнішнього тиску, тобто на збільшення запасу ентальпії: (1.24) Із рівнянь (1.23) і (1.24) випливає, що С v і Ср є функціями стану. Таким чином, істинна ізохорна теплоємність дорівнює частковій похідній внутрішньої енергії системи за температурою при сталому об'ємі, а істинна ізобарна теплоємність дорівнює частковій похідній ентальпії за температурою при сталому тиску. Між Сv і Сp існує різниця. В загальному вигляді вона може бути виражена як: (1.25) де a 1/ V0 (V / T ) p — розширення; 1/ P0 (P / T )v коефіцієнт термічного — термічний коефіцієнт тиску; V0, Ро — відповідно, початковий об'єм і тиск. Встановимо зв'язок між Сv і Ср для ідеального газу. Для цього візьмемо часткову похідну виразу (1.8) за температурою при сталому тиску для одного моля газу. (1.26) Згідно з рівняннями (1.23) і (1.24) 21 (1.27) Підставивши (1.26) у (1.27), дістанемо: (1.28) та Внутрішня енергія ідеальних газів залежить лише від температури не залежить під тиску і об'єму. Згідно з цим (U / T ) p (U / T )v Cv . Оскільки для ідеальних газівPV = RT, то (V / T ) p R і різниця між теплоємностями при сталому тиску та сталому об'ємі дорівнює (рівняння Майєра): C p Cv R (1.29) де R — універсальна газова стала. Теплоємність Ср є більш важливою характеристикою, ніж С v тому що майже всі термодинамічні процеси протікають при сталому тиску. В 1819 році П. Дюлонг та Л. Пті сформулювали правило, згідно з яким атомна ізобарна теплоємність металів приблизно дорівнює Ср = = ЗR, тобто 25 Дж/(мольК). Це значення підноситься до невеликого інтервалу кімнатних температур. Значні відхилення від даного закону спостерігаються для легких елементів, особливо неметалів. Для твердих тіл при низьких температурах різниця Cp-Сv замала. Із підвищенням температури проявляється ангармонізм коливання атомів кристалічної решітки, що приводить до збільшення теплоємності. Для реальних газів, рідин та аморфних тіл користуються емпіричною залежністю теплоємності від температури за різними ступеневими (1.30) (1.31) де а, b, с — емпіричні коефіцієнти, що визначають експериментально. Викопавши інтегрування обох частин рівняння (1.30) від T1, до Т2, отримаємо залежність ентальпії від температури: 22 У твердому матеріалі теплоємність залежить від його структури. Якщо при зміні температури речовини відбуваються структурні перетворення (плавлення, випаровування тощо), то змінюється монотонний характер температурної залежності теплоємності цієї речовини. В широкому діапазоні температур залежність теплоємності багатьох речовин має складний характер. На рис. 1.1 наведена температурна залежність теплоємності для більшості металів. Рис. 1.1. Залежність теплоємності простих тіл від температури 1.4. Залежність внутрішньої енергії та ентальпії від температури Для знаходження виразів температурної залежності внутрішньої енергії та ентальпії необхідно проінтегрувати рішення ( 1 . 2 3 ) та ( 1 . 2 4 ) . в межах від 0 до Т. Тоді іптегруванням зміни внутрішньої енергії отримаємо: T T 0 0 dU C dT v або (1.32) Аналогічно знаходимо залежність від температури для ентальпії: 23 Т T 0 0 dH C p dT , звідси T H 0T H 00 C p dP (1.33) 0 Значення U0 і Но при температурі 0 K не відомі. Фактично обчислюють різницю Um – U0 і HT – H0 за відомими температурними залежностями з урахуванням можливих агрегатних перетворень. Часто за нижню межу інтегрування беруть не нуль градусів, а стандартні умови (Т = 298К, Р = 101,3 кПа). 1.5. Залежність теплового ефекту реакції від температури Візьмемо часткову похідну за температурою від QP= H при Р= соnst або (1.34) Візьмемо часткову похідну за температурою від Qv = U = U 2 – U 1 при V = сопst: або (1.35) Рівняння (1.34) та (1.35) відомі як рівняння Кірхгоффа: температурий коефіцієнт теплового ефекту дорівнює зміні теплоємностей усіх речовин, що беруть участь у реакції. Із рівняння (1.34) випливає: коли зміна теплоємностей процесу додатня, C p для C p 0 , то д( H )/дТ 0, тобто з підвищенням тем24 ператури тепловий ефект зростає і, навпаки, при C p < 0 д( H )/дТ 0 з підвищенням температури тепловий ефект процесу зменшується. Якщо для процесу C p = 0, то д( H )/дТ = 0 і тепловий ефект це залежить від температури. Рівняння (1.34) і (1.35) задають лише залежність теплового ефекту від температури. Щоб визначити тепловий ефект за будь-якої температури, ці рівняння треба проінтегрувати від Т1 до Т2 : (1.36) Якщо в заданому інтервалі температур від Т і до Т2 теплоємність усіх речовин не змінюється, рівняння (1.36) матиме такий вигляд: (1.37) Якщо в інтервалі температур від Т2 до Т1, теплоємність залежить від температури, то теплоємність кожної речовини треба подавати як функцію температури: C p = а + bТ + сТ 2 , і тоді (1.38) Рівняння (1.37) і (1.38) застосовують лише для процесів, в яких відсутні фазові перетворення. Розв'язання цих рівнянь можливе, коли відомий тепловий ефект H T 1 при Т 1 . Нехай Т 1 = 298 К, а Т 2 — Т 1 , то T 0 інтегрування рівняння (1.36) дає: H T0 H 298 C p dT 298 де 0 H 298 визначають за законом Гесса, або Тепловий ефект процесу можна визначити також за рівн яннями (1.39) 25 (1.40) якщо відома різниця ентальпій для всіх речовин, які беруть участь у 0 реакції, та (H T0 H 298 )i (H T0 H 00 ) які можна знайти и таблицях довідників з термохімії. 1.6. Другий закон термодинаміки Перший закон термодинаміки характеризує енергетичні баланси і дає змогу обчислити теплові ефекти хімічних реакцій за стандартних умов (закон Гесса) і за будь-якої температури (закон Кірхгоффа). Але він не відповідає на питання щодо можливості самовільного перебігу того чи іншого процесу. Другий закон термодинаміки ґрунтується па закономірностях, згідно з якими можна знаходити напрям процесу і визначати умови, за яких можливі ті чи інші процеси. Другим закон термодинаміки, так само як і перший, с постулатом. Він сформульований па основі багатовікового людського досвіду. Його можна обґрунтувати методами статистичної термодинаміки. Сфера застосування цього закону обмежена: .інше для макросистем. які складаються з великої кількості частинок. Другий закон термодинаміки мас важливе значення для хімії та різних технологій. Він встановлює можливість, напрям і межу перебігу самовільних процесів. Термодинамічні параметри поділяють па інтенсивні та екстенсивні. Інтенсивні величини не залежать від кількості речовини або маси системи і при взаємодії системи вони прямують до вирівнювання — температура та тиск. Екстенсивні — пропорційні до кількості речовини і при взаємодії системи вони додаються — об'єм, маса, теплоємність. Самовільно можуть відбуватися лише такі процеси, внаслідок яких вирівнюються ті або інші фактори інтенсивності. Рівновазі відповідають однакові значення фактора інтенсивності в кожній частині системи. Для самовільного перебігу процесу мають бути створені умови, які сприяють такому вирівнюванню. Наприклад, для теплообміну потрібні різні температури в різних частинах системи або в системі та навколишньому 26 середовищі. У реальних процесах переважно вирівнюються не один, а кілька факторі в і інтенсивності. М.В. Ломоносов (1749), а пізніше Р. Клаузіус (1850) сформулювали другий закон термодинаміки: «Теплота не може самовільно переходити від холодного тіла до гарячого». Процеси можуть самовільно відбуватись лише в напрямі, який приводить до вирівнювання факторів інтенсивності — теплота може переходити від гарячого тіла до холодного, газ може розширюватись лише з одночасним зниженням тиску, електричний струм протікає від вищого потенціалу до нижчого тощо. У. Кельвін (1851) запропонував інше визначення другого закону: «Неможливо створити пічний двигун другого роду, тобто неможливо побудувати машину, яка б періодично діяла лише за рахунок віднімання теплоти від теплового резервуара». Практично перетворювати теплоту па роботу можна лише частково і тоді, коли в джерелі с теплота високого потенціалу. Якби не було цього обмеження або якби можна було перетворювати па роботу теплоту будь-якого потенціалу, людство могло б використовувати як джерело енергії теплоти морів та океанів. На практиці трапляються процеси, коли треба передати теплоту від менш нагрітих тіл до більш нагрітих. Такий процес здійснюється в холодильних машинах, де теплова енергія відбирається від охолоджувальних тіл і відводиться у навколишній простір з більш високою температурою. Щоб здійснити такий процес, потрібно витратити енергію. 1.6.1. Математичний вираз другого закону термодинаміки Згідно з другим законом термодинаміки неможливо перетворити на роботу всю теплоту, узяту від джерела. Частина її обов'язково витрачається в холодильнику непродуктивно. Коефіцієнт корисної дії (ККД) будь-якого процесу залежить від того, як такий процес відбувається. Найбільшим він буде для зворотного циклу. Так, для циклу Карно, що складається з двох зворотних ізотерм та двох зворотних адіабат, коефіцієнт корисної дії можна представити як (1.41) В загальному випадку для будь-якого циклу (1.42) 27 Знак рівності ( = ) стосується циклу Карно, знак нерівності (<) дійсний для будь-якого циклу, який має місце між температурами T1 і T 2 . Для циклу Карно рівняння ( 1 .4 2 ) можна записати так: або Оскільки теплоту, яку дістала система, беремо зі знаком плюс, а теплоту, яку вона піддала, — зі знаком мінус, перед Q2 треба змінити знак на протилежний: (1.43) Теплоту, поділену на температуру, за якої її одержано або піддано системою, називають зведеною. Рівняння (1.43) показує, що сума зведених теплот циклу Карно дорівнює нулю. Для нескінченно малого циклу Карно Будь-який цикл Карно можна виразити як суму елементарних циклів (1.44) або суму можна замінити інтегралом по замкненому контуру (1.45) Сума зведених теплот для зворотного циклу Карно дорівнює нулю. Для незворотного циклу (1.46) Рівняння (1.46) називають нерівністю Клаузіуса. Розглянемо циклічний процес і позначимо на ньому точки А і Б, які означають відповідний етап системи: 28 Тоді або (1.47) Іншими словами, сума зведених теплот (інтеграл) під час переходу системи рівноважним шляхом від стану (А) до стану (Б) не залежить від шляху процесу, а залежить лише від початкового та кінцевого її етапів. Інтеграл елементарних теплот (зведених) рівноважного процесу дорівнює приросту функції стану, яку називають ентропією і позначають літерою 5: (1.48) В середині XIX століття (1854 р.) на основі другого начала термодинаміки Клаузіус показав, що існує така термодинамічна функція, яка є функцією етапу, і зміна якої для зворотного ізотермічного переходу теплоти дорівнює приведеній теплоті процесу. Ця величина отримала назву ентропії. В перекладі з грецької означає «еn» — в, «trоре» — поворот. Тобто повернення всередину. Ентропію треба розглядати як міру переходу енергії в тому чи і н шому процесі в таку форму енергії, з якої вона не може самовільно переходити в інші форми. Розглянемо ізольовану систему, що складається з двох тіл А і В з температурою Та і Тb відповідно. Температура тіла A перевищує температуру B, тобто Тa > ТB. Від тіла А до тіла В перейшла теплота Q. Для тіла А цей перехід спричинив зміну його ентропії. а для тіла В 29 Загальна .зміна ентропії системи дорівнює сумі цих змін: Оскільки Та > Тв, права та ліва частина рівняння більші під нуля: (1.49) Отже, в ізольованих системах теплота від гарячого тіла до холодного переходить зі збільшенням ентропії системи. У загальному вигляді другий закон термодинаміки: (1.50) Будь-який самовільний процес відбувається доти, доки не настане рівновага. Водночас зростатиме ентропія. Коли ізольована система досягне рівноваги, ентропія стане максимальною. Отже, про напрям хімічної реакції можна дніти висновку виходячи зі змій ентропії в ізольованій системі. У стані рівноваги ентропія матиме максимальне значення і доки ізольована система перебуватиме у рівновазі, її ентропія не зміниться: (1.51) Ентропія, с мірою невпорядкованості стану системи. Вона збільшується для процесів плавлення, кипіння, розчинення, сублімації, а також для процесів, які відбуваються зі збільшенням об'єму, тощо. З наведених прикладів випливає, що ентропія збільшується при переході речовин зі стану з меншою енергією у стан з більшою. Навпаки, усі процеси, пов'язані зі збільшенням впорядкованості (охолодження, кристалізація з розчинів), супроводжуються зменшенням ентропії. 1.6.2. Ентропія та ймовірність Нехай простір посудини поділено позначкою па дві рівні частини, у кожній з яких знаходиться по одній молекулі газу. Якщо усунути позначку, то ймовірність того, що обидві рухомі молекули опиняться із якійсь одній частині, дуже велика. Це означає, що існують процеси, які вступають у протиріччя з другим началом. Збільшимо кількість молекул удвічі. Ймовірність перебування всіх чотирьох молекул в одній частині 30 простору значно зменшиться. Розмірковуючи далі, дійдемо висновку: що менша кількість частинок, то ймовірніші процеси, які не задовольняють друге начало. Друге начало справджується лише для макросистем і має статичний характер. Кожний стан характеризується певною ймовірністю, яка збільшується у процесі. При досягненні системою рівноваги її термодинамічна ймовірність с максимальною. Макростан газу визначається такими його параметрами, які можна безпосередньо виміряти: об'ємом, тиском, температурою. Якби можливо було в даний момент чітко зафіксувати положення і швидкості (або імпульси) усіх молекул, то був би відомий мікростан газу. Здійснити це практично неможливо. Залишається констатувати, що одному макростану відповідає велика кількість мікростанів, які відрізняються один від одного положеннями і швидкостями окремих молекул. Чим більше число мікростанів, що відповідають даному макростану, тим воно простіше виникає. Термодинамічною ймовірністю (W) називають число мікростанів, ідо відповідають даному макростану. Ймовірність є критерієм, за допомогою якого можна визначити напрям процесу та умови рівноваги системи. Оскільки ентропія та термодинамічна ймовірність у стані рівноваги набувають максимального значення, між ними встановлено зв'язок (рівняння Больцмана) S k ln W (1.52) де к — стала Больцмана. Розвиток статистичної термодинаміки дав можливість розрахувати ентропію різних речовин па основі даних про їх внутрішню структуру. Ентропію можна розглядати як суму складових, що належать до різних форм енергії руху частинок: S S пост Sоберт S колив Sел ..., тобто дорівнює сумі ентропій поступального, обертального та коливального рухів, ентропії електронів тощо. Зміна ентропії реакції визначається різницею суми ентропії продуктів реакції і суми ентропії початкових речовин. Для хімічної реакції типу: aA + bB = cC + dD при стандартних умовах зміна ентропії 31 де 0 S 298 — зміна ентропії одного моля відповідних речовин при стандартних умовах. 1.6.3. Статистичний характер другого закону термодинаміки Другий закон термодинаміки не є абсолютним законом природи (як і перинні закон), а мас статистичну природу і викопується з високим ступенем точності для систем з великою кількістю часток. Р. Клаузіус дотримувався думки, що другий закон є абсолютним законом природи, і сформулював дна таких положення: енергія Всесвіту стала: ентропія прямує до максимуму. Зростання ентропії, за Клаузісом, означає, що через деякий час ентропія Всесвіту буде близькою до максимальної. Всі процеси зупиняться, розвиток Всесвіту також зупиниться і настане його теплова смерть.. Проте усі ці ствердження Клаузіуса невірні. Немає жодних підстав розглядати Всесвіт як ізольовану систему. Всесвіт нескінченний і не можна уявити, що коли-небудь настане теплова рівновага. За час існування Всесвіту така рівновага вже мала б настати. З погляду матеріалістичної діалектики Всесвіт існує вічно. Не можна уявити його початок або кінець. Немає жодних підстав поширювати результати, одержані за земних умов, па Всесвіт. 1.6.4. Зміна енергії в різних процесах Для незворотних процесів зміна ентропії пов'язана з теплотою процесу нерівностями (1.49), (1.50). Тому для цих процесів ентропію визначити неможливо. Але зміна ентропії для зворотного та незворотного процесів однакова, оскільки ентропія с функцією стану. Щоб розрахувати зміну ентропії для реального незворотного процесу, треба цей процес умовно провести зворотно і обчислити зміну ентропії згідно з рівнянням (1.48) для зворотного процесу. Для ізотермічного процесу (Т = соnst) при фазових перетвореннях (1.53) де L — теплота фазового перетворення. Підставивши в рівняння (1.48) вираз для теплоти при сталому об'ємі Qv отримаємо зміну ентропії для ізохорного процесу: 32 (1.54) Якщо в даному інтервалі температур С у = соnst, то (1.55) При зміні температури речовини для ізобарного процесу (1.56) Якщо С Р = соnst, то Оскільки для ідеальних газів dU = С V dТ, а робота розширення A PdV , то рівняння ( 1 . 4 ) набуде вигляду: (1.57) що є об'єднаним виразом першого та другого термодинаміки. Замінемо P = RT/V, розділимо на Т вираз (1.57) і дістанемо законів (1.58) або (1.59) Отже, ентропія ідеального газу зростає при збільшенні температури та об'єму. Комбінуючи рівняння (1.59) з рівнянням Менделєєва-Клапейрона, дістаємо: (1.60) Рівняння (1.59) та (1.60) справджуються лише для ідеальних газів. Таким чином, ентропія с характеристичною функцією, за допомогою якої можна виразити термодинамічні властивості системи. 33 Зміна ентропії характеризує напрям процесу лише в ізольованих системах. Більшість хімічних процесів відбуваються при незмінних температурах і тиску, у відкритих апаратах або при незмінних температурах і об'ємі у закритих апаратах (в автоклавах). У цих випадках зручніше обчислювати інші характеристичні функції. 1.6.5. Термодинамічні потенціали Важливою властивістю закрито/ системи є її здатність виконува ти роботу. Найчастіше під цим терміном розуміють роботу розширення (1.9). Більш цінною в деяких випадках виявляється корисна робота, що не спрямована па розширення, а з'являється після віднімання роботи розширення від загальної роботи: При сталості певних пар параметрів: (механічних — Р, V та термічних — Т, S), величина корисної роботи Ак може бути представлена як різниця значень деяких функцій станів. Похідні цих функцій станів називаються термодинамічними потенціалами. Виразимо об'єднане рівняння першого та другого законів термодинаміки: через корисну роботу: (1.62) Для різних процесів цей вираз матиме різний вигляд. 1. Ізохорно-ізоентропійний процес (S,V = сопst). Для цього процесу відсутня зв'язана енергія Гельмгольця (ТdS) та робота розширення, тому ізохорно-ізоентропійні процеси відбуваються самовільно зі зменшенням внутрішньої енергії системи мінімальною: Aк dU . І при рівновазі вона стає (1.63) Зміна внутрішньої енергії і є в даному випадку термодинамічним потенціалом. 2. Ізобарно-ізоентропійний процес (Р, S= сопst). Для нього 34 характерна відсутність зв'язаної енергії Гельмгольця, і корисна робота Aк dU PdV , або Aк dH За цих умов самовільно відбуваються процеси зі зменшенням ентальпії, яка в стані рівноваги стає мінімальною: (1.64) Зміна ентальпії і є в даному процесі термодинамічним потенціалом. 3. Ізохорно-ізотермічний процес (V,Т = сопst). Цей процес ближчий до реальних. Для пошуку відповідного потенціалу, що описує умови рівноваги, введено функцію U — ТS, яку позначають літерою F і називають вільною енергією Гельмгольця. Тоді із рівняння (1.62) отримуємо: (1.65) В ізохорно-ізотермічних умовах самовільні процеси відбуваються зі зменшенням енергії Гельмгольця: (1.66) Зміна вільної енергії Гельмгольця є термодинамічним потенціалом при ізохорно-ізотермічному процесі. 4. Ізобарно-ізотермічний процес (Р, Т = соnst). Більшість технологічних процесів відбувається за умов сталого тиску та температури. Корисна робота при цьому процесі має такий вигляд (див. рівняння (1.62)): Функцію (H — ТS) позначають літерою G і називають вільною енергією Гіббса. При ізобарно-ізотермічних умовах самовільні процеси проходять зі зменшенням вільної енергії Гіббса і в момент рівноваги зміна цієї енергії досягає мінімального значення: (1.68) Зміна вільної енергії Гіббеа є термодинамічним потенціалом при 35 ізобарно-ізотермічному процесі. Зв'язок між термодинамічними потенціалами можна зобразити графічно: Умови термодинамічної рівноваги системи в різних термодинамічних процесах описуються рівняннями: (1.72) Таким чином, у стані рівноваги термодинамічні потенціали мають мінімальні значення за відповідних сталих змінних (Р, V, Т, S), а ентропія мас максимальне значення за сталих внутрішньої енергії та об'єму системи. 1.6.6. Характеристичні функції Характеристичною функцією називається функція стану системи, за допомогою якої або її похідних можна виразити інші властивості системи. В термодинаміці найчастіше використовують такі основні характеристичні функції: (1.73) Тобто U f ( S , V ); H f ( S , P); F f (V , T ); G f ( P, T ). Кожна з цих функцій дає повну термодинамічну характеристику системи. Запишемо повні диференціали характеристичних функцій: 36 Отже, цими рівняннями встановлюється взаємозв'язок характеристичними функціями та їх частковими похідними. між 1.6.7. Термодинаміка хімічних реакцій Розглянемо умовну хімічну реакцію Згідно із законом Гесса зміна вільної енергії Гіббса для даної реакції мас такий вигляд: (1.82) Введемо поняття стандартної вільної енергії G f , — зміни величини 0 G у процесі утворення хімічної сполуки з простих речовин у найбільш стійкій формі за стандартних умов. Значення стандартної вільної енергії Гіббеа для різних хімічних сполук наведені у відповідних довідниках. Для стандартної вільної енергії також справедливе рівняння Гесса (1.83) З умов термодинамічної рівноваги сиcтеми (1.72) випливає важливий висновок: при даній температурі хімічна реакція можлива, якщо зміна вільної енергії Гіббcа буде від'ємною. Отже, Gx. p. 0 — можливий перебіг самовільної реакції Gx. p. 0 — умови рівноваги реакції 37 Gx. p. 0 — самовільно буде відбуватися зворотна реакція. Приклади: Отже, можливість самовільного перебігу цієї хімічної реакції малоймовірна Проаналізуємо можливість перебігу хімічних реакцій у різних термодинамічних процесах. У загальному вигляді зміна вільної енергії Гіббса хімічної реакції подається рівнянням (1.84) З рівняння видно, що зменшення вільної енергії внаслідок хімічної реакції може відбуватися як за рахунок зменшення ентальпії, так і за рахунок зростання ентропії. Різні випадки можливостей перебігу хімічних реакцій наведено в табл. 1. Таблиця 1. Можливість перебігу хімічної реакції. Аналогічно можна записати рівняння для зміни ентропії внаслідок хімічної реакції (1.85) Підставимо рівняння стану газів V = RТ/Р у рівняння (1.81), 38 Звідси можна отримати Після інтегрування цього рівняння маємо: Позначимо сталу даного рівняння як G°. Тобто це вільна енергія 1 моля газу за стандартних умов, або стандартна енергія. Отже, (1.86) Аналогічно, отримаємо використовуючи рівняння стану газів та (1.87) (1.79), звідси Після інтегрування маємо (1.88) або (1.89) Отже, за відомої зміни тиску чи об'єму газу при сталій температурі для розрахунків зміни вільної внутрішньої енергії використовують рівняння ( 1 .87 ) та (1.89). Запишемо рівняння для термодинамічних потенціалів у формі: та зв'язок часткових та(1.81) похідних цих потенціалів з ентропією (1.80) 39 Комбінуючи ці математичні вирази, отримаємо рівняння: (1.90) що дістали назву рівняння Гіббса-Гельмгольця. Велике практичне значення мають розрахунки зміни цих потенціалів за температурою. Розглянемо ізотермічний перехід системи між двома станами 1 та 2. Для кожного з них запишемо рівняння (1 .90): Звідси зміна вільної енергії Гельмгольця (1.91) Аналогічно отримаємо .рівняння для зміни цільної енергії Гіббса (1.92) Отже, рівняння (1.91) та (1.92) використовують для розрахунків зміни ізобарно-ізотермічного та ізохорно-ізотермічного потенціалів при різних температурах, коли відомі зміна внутрішньої енергії та зміна ентальпії при одній якійсь температурі, наприклад, при стандартній. 1.6.8. Розрахунки термодинамічних потенціалів 1. Ідеальні гази Якщо процес відбувається за сталої температури, для 1 моля ідеального газу вираз (1.73) запишемо як: (1.93) Згідно з рівнянням стану ідеального газу Р = НТ/У, маємо 40 (1.94) Після інтегрування (1.95) 2. Реальні гази Для розрахунків термодинамічних потенціалів реальних газів використовують такі вирази, що й для ідеальних газів, але з введенням нової термодинамічної величини — фугітивності. Фугітивністю f називається величина, підстановка якої замість тиску у вираз ізобарно-ізотермічного потенціалу (1.86) ідеального газу робить його справедливим для реального газу: (1.97) Фугітивність є по суті ефективним тиском. Що вищий тиск, їх більше відрізняється від нього фугітивність. Відношення фугітивності до тиску реального газу наривають коефіцієнтом фугітивності. (1.98) (1.99) Для одного моля реального газу вираз (1.97) набуває вигляду (1.100) Існує декілька експериментальних методів обчислення фугітивності та коефіцієнта фугітивності реальних газів. 3. Реальні розчини Для одного моля і-го компонента ідеального розчину рівняння (1.86) має вигляд: (1.101) де N1— мольна частка і — того компонента розчину. У реальних розчинах відхилення від законів ідеальних розчинів враховується за допомогою активності. Активність а — це величина, підстановка якої замість концентрації (мольної частки) в термодинамічні рівняння ідеального розчину робить їх справедливими для реального розчину. 41 Вона враховує взаємодію між молекулами розчиненої речовини, між цими молекулами і молекулами розчинника (сольватація), а також інші явища, якими відрізняються реальні розчини від ідеальних. Для розрахунку ізобарного потенціалу і-го компонента реального (.неідеального) розчину замість концентрації (мольної частки Ni ) підставляють активність а 1 цього компонента: (1.102) Величину, яка показує наскільки активність відрізняється від концентрації, називають коефіцієнтом активності Ji: або (1.103) (1.104) 1.7. Хімічний потенціал Досі ми розглядали хімічну термодинаміку однокомпонентних систем. На практиці маємо справу із сумішами речовин у різних пропорціях. У цьому разі па значення вільної енергії системи впливає не тільки температура і тиск, а й концентрація компонентів суміші. Подамо вільну енергію суміші як функцію температури, тиску та концентрації компонентів п 1, п 2, n 3... Запишемо повний диференціал вільної енергії в часткових похідних де ni — число молей всіх компонентів суміші; п j— число молей всіх компонентів суміші за винятком п j. Враховуючи, що рівняння (дG/дТ) Р = —S та (дG/дР) T = V дійсні для всіх компонентів суміші, попереднє рівняння можна подати як 42 (1.105) Вираз (дG/дп i )T, P, nj являє собою парціальну вільну енергію, що називається хімічним потенціалом i . Отже, (1.106) Аналогічно можна показати, що (1.107) З цих рівнянь випливає, що хімічний потенціал — це приріст будьякого термодинамічного потенціалу суміші при додаванні 1 моля і-го компонента до нескінченно великої кількості суміші при сталих температурі, тиску та вмісту інших компонентів у суміші. З урахуванням рівнянь (1.106) та (1.107) рівняння (1.105) набуде вигляду: (1.108) При сталих тиску та температурі в умовах термодинамічної рівноваги маємо: 1 i d ni 0 (1.109) i Це рівняння дістало назву рівняння Гіббса – Дюгема. Для суміші газів можна записати: Gi Gi0 RT ln Pi (1.110) де Gi та Gi – парціальні вільні енергії; Р і - парціальній тиск і – го компонента суміші газів. Таке саме рівняння дійсне і для хімічних потенціалів: 0 i i0 RT ln Pi де (1.111) і0 - стандартний хімічний потенціал і-го компонента газу. Для розчинів можна записати аналогічне рівняння i i0 RT ln N i m i .c i , 43 де і ,mі cі - концентрація і-го компонента розчину, подана в мольних частках, моляльність або молярність, відповідно. Для бінарного ідеального розчину, наприклад, можна записати: i,1 i0 RT ln N i,1 , i,2 i0 RT ln N i,2 . звідси i,2 i0,1 RT ln( N i,2 / і,1 ) Для обчислення хімічного потенціалу реального бінарного розчину в цих рівняннях треба замість концентрацій підставити активності і – го компонента, i,2 i0,1 RT ln( а i, 2 / а і,1 ). У стандартному стані активність розчинника приймається за одиницю, аі = 1. Отже, i i0 RT ln а i (1.112) В даному випадку активністю і-го компонента розчину називається величина, яку треба підставити у вираз для хімічного потенціалу цього компоненти в ідеальному розчині, щоб отримати дійсне значення хімічного потенціалу і-го компонента реального розчину. Фізико-хімічні властивості розчинів залежать від активності розчинника та розчиненої речовини. Існує кілька способів визначення активності розчинів: за парціальним тиском пари леткої розчиненої речовини, тиском пари розчинника, коефіцієнтом розподілу між парою та розчином, зниженням температури замерзання або підвищенням температури кипіння розчинів, осмотичним тиском тощо. Розглянемо як приклад визначення активності розчинника через його тиск над розчином. Запишемо вирази хімічного потенціалу пари самого розчинника (|і") та його пари у розчині ( 44 0 ). Згідно з (1.110) маємо: Для окремих компонентів цього розчину маємо: звідси Якщо вибрати стандартний стан а 0 = 1, Цей вираз є дуже корисним при розгляді активності не тільки розчинів, а й активності речовин в адсорбованому стані, де встановлюється рівновага між тиском пари та адсорбованою фазою. 1.8. Хімічна рівновага Під час хімічної реакції через деякий час встановлюється стан рівноваги, коли швидкості прямої та зворотної реакції однакові. Хімічна термодинаміка дає можливість визначити концентрації реагентів у суміші з рівновагою, вплив па них зовнішніх умов і передбачити максимальний вихід корисного продукту, що мас велике практичне значення. Виведемо співвідношення між концентраціями реагентів у рівноважній суміші. Розглянемо реакцію в газовій фазі (газ ідеальний) при сталих температурі та тиску, для якої справджується вираз де (1.113) Gi — ізобарний потенціал 1 моля і-го компонента; nі - число молей цього компонента. Для идеального газу тоді (1.114) Зміна ізобарного потенціалу становить 45 або (1.115) де G 0 — стандартна зміна ізобарного потенціалу. Після досягнення рівноваги G 0 = 0. Для ізотермічного процесу RТ = соnst і G 0 = соnst. Вираз у дужках також дорівнюватиме сталій величині: (1.116) де Кр — константа рівноваги хімічної реакції, виражена через парціальні тиски всіх компонентів, яка не залежить від загального і парціального тисків газів. Для умовної хімічної реакції (1.117) вираз(1.116) матиме вигляду де РD , РR, РA, РB — парціальні тиски речовин; (1.118) Рівняння (1.118) с математичним виразом закону діючих мас, який відкрито Гульдбергом і Вааге у 1807 р. Із нього випливає, що Кр дає кількісну оцінку рівноважного стану. Коли числове значення Кр набагато більше за одиницю, рівновага системи зміщується в напрямі утворення продуктіи реакції (вправо), а коли значення Кр менше за одиницю, у суміші значно більше початкових речовин і рівновага реакції зсувається вліво. При незмінній температурі парціальні тиски прямо пропорційні концентраціям. Якщо концентрацію виразимо в молях на літр, то Рі = C i R Т. 46 Замінюючи в рівнянні (1.118) парціальні тиски на концентрації, отримаємо Позначивши (1.119) де KC— константа рівноваги виражена через концентрацію реагуючих речовин, отримаємо (1.120) У загальному випадку константа рівноваги, виражена через концентрації, не дорівнює константі, представленій через парціальні піски. Вони однакові, якщо реакція проходить без зміни кількості молекул ( п = 0). Якщо реакція відбувається в суміші реальних газів, то (1.118) матиме вигляд (1.121) де Кf — константа рівноваги, виражена через фугітивність; f D , f R , f A , f B — фугітивності газів. Для неідеального розчину замість концентрації використовуємо активність 1 : (1.122) Рівняння (1.118), (1.119), (1.121), (1.122) є математичним виразом закону діючих мас, який в найпростішому випадку для ідеальних газових реакцій можна визначити таким чином: відношення добутку рівноважних концентрацій (або парціальних тисків) продуктів реакції, узятих в ступенях, що дорівнюють їх стехіометричним коефіцієнтам, до аналогічного добутку вихідних речовин при заданій температурі є величиною сталою. Він показує, що за умов рівноваги парціальні тиски (або концентра ції) усіх реагуючих 47 речовин взаємопов'язані. Неможливо змінити Р,, С, жодної з речовин, щоб не змінилися парціальні тиски (концентрації) усіх інших речовин так, що К р (К c ) отримав своє попереднє значення за даних умов. Отже, до основних властивостей хімічної рівноваги належать такі умови: - збереження стану хімічної рівноваги при сталості зовнішніх факторів; - мобільність рівноваги, тобто самовільне повернення системи в стан рівноваги коли перестає діяти фактор, що викликав зсув рівноваги; - динамічний характер рівноваги, тобто встановлення та підтримка рівності швидкостей прямої і зворотної реакцій; - можливість досягнути рівноваги з двох протилежних напрямків; - мінімум вільної енергії. 1.8.1. Рівновага в гетерогенних системах Гетерогенними називаються реакції, в яких реагенти перебувають у різних фазах. Наприклад, реакція відновлення заліза в оксиді вуглецю Для встановлення умов гетерогенної хімічної рівноваги розглянемо систему, що складається з двох фаз: а і . У кожній із цих фаз міститься і-й компонент, число молей якого становить nia та ni . Вільна енергія Гіббса кожної фази системи є: Повний диференціал вільної енергії Гіббса для кожної фази: (1.123) (1.124) Припустимо, що при сталій температурі та тиску внаслідок хімічної реакції деяка дуже мала кількість компонента і dn1. переходить з фази у фазу . Концентрація реагентів при цьому не змінюється. Тому рівняння (1.123) і 48 (1.124) можна записати як dG i dni і dG i dni Загальна зміна вільної ентальпії гетерогенної системи в умовах рівноваги Подамо перехід і-ї компоненти з фази α в β як (1.125) Тоді попереднє рівняння можна записати так або (1.126) Рівняння (1.126) визначає умову гетерогенної хімічної рівноваги: хімічні потенціали і-го компонента системи в різних фазах однакові. Отже, рівновазі гетерогенних систем відповідає рівність хімічних потенціалів кожного компонента в усіх фазах та мінімальне значення одного з термодинамічних потенціалів або максимальне значення ентропії всієї системи за відповідних умов. Встановлення рівноваги між фазами гетерогенної системи називається фазовою рівновагою. 1.8.2. Напрямок фізико-хімічних перетворень у гетерогенних системах До встановлення термодинамічної рівноваги хімічні реакції проходять у нерівноважних умовах. Знайдемо умови переходу і-го компонента суміші з фази а в . Припустимо, що деяка мала кількість і-го компонента сіп, переходить з фази а в при сталій температурі та тиску за незмінних інших умов. Умова перебігу будь-якого самовільного процесу є dG < 0, тобто 49 З урахуванням формули (1.125) запишемо або ( i ia )dni 0 . Оскільки ia dni i dni 0 dni 0 то ( i i ) 0 , a або (1.127) Це головна умова міжфазного переходу будь-якого компонента суміші: для того щоб і-й компонент переходив з однієї фази в іншу, необхідно, аби його хімічний потенціал у цій фазі був більшим за його потенціал в іншій фазі. Інакше можна стверджувати, що при взаємодії двох фаз у гетерогенній системі буде спостерігатися самовільний перехід і-го компонента з фази з більш високим хімічним потенціалом у фазу з меншим потенціалом до встановлення рівноваги. 1.8.3. Рівняння ізотерми хімічної реакції Розглянемо умовну хімічну реакцію для ідеального газу при Т — = сопst і сталому парціальному тиску всіх речовин, які беруть участь у реакції. Дана реакція характеризується зміною ізобарного потенціалу (1.128) У стані рівноваги G = 0, а Підставляючи ці значення в (1.128), дістанемо (1.129) (1.130) Якщо Р і — парціальні тиски компонентів рівноважної системи, Рі — нерівноважної, то (1.128) матиме вигляд (1.131) 50 Це є математичним виразом рівняння ізотерми хімічної реакції, або рівняння Вант-Гоффа. Для реакції (1.117) або у загальному вигляді (1.132) де Із рівняння ізотерми хімічної реакції (1.131) видно, що величина і знак ізобарного потенціалу реакції залежить від відносних значень ПР і К Р (Р = сопst; Т = сопst). G < 0, тобто процес необоротний самовільний. Реакція буде проходити зліва направо. При П р ! = К р G = 0, реакція досягла рівноважного стану. При П р! > Кр маємо G > 0 — При Пр! < Кр маємо процес необоротний самовільний. Реакція відбуватиметься у зворотному напрямі. За допомогою рівняння ізотерми хімічної реакції можна визначити напрям реакції, якщо відомі константа рівноваги і початковий вміст реагентів у системі. Різні речовини виявляють різну здатність вступати в хімічні реакції. Таку здатність називають хімічною спорідненістю. Хімічну спорідненість визначають зміною термодинамічного-потенціалу або максимальною роботою хімічної реакції. 1.8.4. Залежність хімічної рівноваги від температури Зі зміною температури рівновага в системі порушується. Тому константа рівноваги с функцією температури. Візьмемо похідну за температурою від (1.92): 51 звідси (1.133) Вираз (1.133) називають ізобарою хімічної реакції. Для процесів, що відбуваються при V = сопst, аналогічно (1.134) Це рівняння ізохори хімічної реакції. Рівняння ізобари та ізохори у диференціальній формі дають залежність константи рівноваги реакції від температури для суміші ідеальних газів. Якщо реакція відбувається в суміші реальних газів, то в рівнянні (1.133) К Р потрібно замінити на Кf (1.135) Згідно з рівняннями (1.133) —(1.135) можна передбачити і оцінити (кількісно та якісно) залежність константи рівноваги від температури. Якщо H > 0 (реакція ендотермічна), температурний коефіцієнт константи також додатний (dlпКр/dТ) > 0. Тобто зі збільшенням температури константа рівноваги ендотермічної реакції завжди збільшується і рівновага завжди зсувається ви рано. Якщо H < 0, то (dlпКр/dТ) < 0 і рівновага зсувається в бік вихідних речовин (тобто вліво). Коли Н = 0 константа рівноваги реакції КР не залежить від температури. До аналогічних висновків доходимо з принципу лабільної рівноваги ЛeШательє: якщо на рівноважну систему діяти зовнішніми факторами, то в пій матиме місце зміщення рівноваги в напрямі послаблення зовнішньої дії. Для екзотермічної реакції синтезу аміаку При підвищенні температури рівновага зміщується так, щоб послабити дію температури. Під час реакції поглинатиметься теплота — розпад аміаку па нітроген і гідроген. Підвищення температури для даної реакції призведе до зміщення рівноваги вліво. Для практичного використання рівняння (1.133) або (1.135) 52 інтегрують за умови, що Н = соnst: (1.136) Сталу В знаходять після експериментального визначення константи рівноваги. Якщо в заданому інтервалі температур тепловий ефект не істотно залежить від температури, у результаті інтегрування (1.133) отримаємо: Тьомкін і Шпарцман запропонували інший метод розрахунку константи хімічної рівноваги. Як відомо, для будь-якої температури: (1.137) де 0 0 H 298 , S 298 — довідкові дані. Підставивши ці вирази в рівняння G0 RTInK p отримаємо 1.9. Третій закон термодинаміки Інтегруючи ізобару або ізохору хімічної реакції, неможливо отримати вираз, за допомогою якого визначається константа рівноваги залежно від теплового ефекту хімічної реакції. При інтегруванні з'являється стала, яку визначають експериментально. Хімічна термодинаміка дає можливість розрахувати сталу рівноваги без проведення дослідів Для цього необхідно знати абсолютні значення ентропій хімічних сполук, які беруть участь у реакції. 53 За допомогою експериментальних даних можна встановити залежність теплового ефекту реакції під температури, наприклад криву H = f(Т) (рис. 1.2 ). Залежність G = f(Т) позбавлена такої невизначеності через появу сталої інтегрування в рівнянні (1.136). Тому на рис. 1.2. матимемо низку кривих, кожна із яких відрізняється від решти константою інтегрування термодинамічних рівнянь. Із рівняння (1.137) випливає, що при наближенні температури до абсолютного нуля S H .Оскільки ентропія не може безперервно зростати, то термодинамічна ймовірність W (1.52) в етапі рівноваги набуває сталого максимального значення. Рис. 1.2. Залежність теплового ефекту реакції від температури G = f(Т) виходять з однієї точки. Щоб визначити положення кривої G = f(Т) ,треба знати сталу інтегрування В Отже, криві H = f(Т) і (або Kp при однаковій температурі). З огляду на це виникла потреба обчислити сталу В на основі якоїсь загальної властивості тіл. Було встановлено, що при наближенні температури до абсолютного нуля властивості тіл дедалі менше залежать від температури. Це явище називають виродженням. У виродженому стані тіла ніби втрачають зв'язок зі світом теплових явищ. Значення температур, 54 при якій настає виродження, різне для різних речовин: для алмазу воно дорівнює 90K, для свинцю — 2K. При цих температурах властивості, ідо залежать від температури (об'єм, енергія, тощо) при вимірюванні, мають однакові значення, а температурні коефіцієнти (ентропія, теплоємність) поблизу абсолютного нуля дорівнюють нулю. Це дало змогу В.Ф. Нернсту дійти висновку, що при абсолютному пулі температури теплоємність всіх тіл дорівнює нулю; при виродженні внутрішня енергія і ентальпія не залежать від температури і набувають однакових значень: H U G Цей вираз відомий як теплова теорема Нернста і він є одним із визначень третього закону термодинаміки, який характеризує загальні закономірності поведінки речовин поблизу абсолютного нуля температури. Теплова теорема не погребує доведення і є постулатом, який базується па експериментальних даних про незалежність від температури багатьох властивостей речовий поблизу абсолютного нуля Отже, при абсолютному пулі Для реакцій, ідо відбуваються у конденсованих системах, при наближенні температури до абсолютного нуля криві G = f(Т) і H = f(Т) виходять з однієї точки і мають спільну дотичну, паралельну осі температур (рис. 1.3). Друге ствердження третього закону термодинаміки (постулат Планка) ґрунтується па тому, що ентропія індивідуального кристалічного тіла (ідеального твердого тіла) при абсолютному пулі дорівнює нулю. ідеальним твердим тілом називають речовину з ідеальною кристалічною решіткою, и якій усі вузли зайняті атомами або молекулами. Для твердих розчинів та склоподібних речовин ентропія при абсолютному нулі не дорівнює нулю. 55 У математичній формі постулат Планка має вигляд: ОТЖЕ (1.138) Тому криві H = f(Т) і G = f(Т) мають спільну дотичну. Із постулату Планка випливає ряд наслідків: 1. Для абсолютної ентропії ідеального твердого тіла (1.139) 2. При абсолютному нулі теплоємність ідеального твердого тіла дорівнює нулю: (1.140) 3. Жодні процеси не можуть знизити температуру тіла до абсолютного нуля (принцип недосяжності абсолютного нуля). Звідси випливає ще одне визначення третього закону термодинаміки: неможливо побудувати машину (вічний двигун третього роду), яка б працювала за рахунок охолодження тіла до абсолютного нуля. Контрольні запитання 1. Охарактеризуйте становлення фізичної хімії як самостійної науки. Предмет та завдання дисципліни. Основні розділи класичної фізичної хімії. 2. Предмет загальної та хімічної термодинаміки. Чому фізична хімія є теоретичною базою будь-якого технологічного процесу?Дати визначення таких понять: «термодинамічна система», «термодинамічний стан системи», «екстенсивні та інтенсивні параметри і функції стану термодинамічної системи», «термодинамічний процес». Класифікація термодинамічних систем. Охарактеризувати теплоту та роботу як форми обміну енергією між 56 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. термодинамічною системою і навколишнім середовищем. Охарактеризуйте поняття «внутрішня енергія термодинамічної системи». Чому не можна визначити її абсолютну величину? Характеристика двох форм передачі енергії в мікро- та макротермодинамічиих процесах, принципова різниця між цими формами. На прикладі процесу стиснення-розширення ідеального газу в ізольованій термодинамічній системі довести, що внутрішня енергія є функцією стану термодинамічної системи. Чому не можна створити вічний двигун першого роду? Які визначення першого закону термодинаміки ви знаєте? Аналітичний вираз закону для мікро- та макротермодинамічних кругових, ізохорних, ізотермічних та ізобарних процесів. Довести, що ентальпія є функцією стану термодинамічної системи. Дати визначення понять «ентальпія утворення» та «ентальпія горіння» хімічних речовин. Одиниці вимірювання цих величин. Фізичний зміст поняття «теплоємність». Дати визначення понять «середня теплоємність», «питома теплоємність», «молярна теплоємність», «істинна теплоємність» речовини. Залежність цієї величини від температури, одиниці вимірювання. Ентальпія та способи її визначення. Навести термодинамічне доведення закону Гесса та наслідків цього закону. Навести термодинамічне доведення закону Кірхгоффа у диференційній та інтегральній формах без урахування та з урахуванням залежності теплоємності речовин від температури. Чому не можна створити нічний двигун другого роду? Па прикладі ізотермічного кругового процесу розширеннястиснення ідеального газу ц ізольованій системі довести, що ентропія є функцією стану термодинамічної системи. Одиниці вимірювання ентропії. Мимовільні та немимовільні, зворотні та незворотні процеси. Статистичне обґрунтування самовільного перерозподілу енергії між роботою та теплом. Формулювання другого закону термодинаміки, його аналітичний вираз для зворотних та незворотних процесів. 57 16. Фізичний зміст ентропії, встановити кількісний вплив температури на ентропію без урахування та з урахуванням залежності теплоємності речовин від температури. 17. Чому на підміну від інших функцій стану для ентропії можна розрахувати її абсолютну величину? 18. Охарактеризувати межі застосування другого закону термодинаміки для характеристики напрямку самовільного процесу. 19. Отримати об'єднане рівняння першого та другого законів термодинаміки та аналітичний вираз характеристичної функції, термодинамічного потенціалу і фундаментальних рівнянь для адіабатно-ізохорних та адіабатно-ізобарних процесів в ізольованих термодинамічних системах. 20. Отримати аналітичний вираз характеристичної функції, термодинамічного потенціалу і фундаментальних рівнянь для ізохорно-ізотермічних і ізобарно-ізотермічних процесів в закритих термодинамічних системах. Довести, що вільна енергія Гельмгольца та вільна енергія Гіббса є функціями стану термодинамічної системи. 21. Довести, що робота рівноважних термодинамічних процесів с максимальною та як вона пов'язана з величинами ізохорного й ізобарного потенціалів. 22. Довести рівняння максимальної роботи Гіббса-Гельмгольца та охарактеризувати їх практичне використання. 23. Які способи оцінки хімічної спорідненості сполук ви знаєте? Охарактеризувати їх недоліки, умови застосування. Яким чином можна провести кількісну характеристику хімічної спорідненості сполук? 24. Чому не можна створити вічний двигун третього роду? Формулювання третього закону термодинаміки, постулат Планка та наслідки постулату. 25. Чому не можна досягнути величину абсолютного нуля температур за шкалою Кельвіна? 26. На прикладі розгляду рівноважного процесу І2(твердий) І2(пара) охарактеризувати ізобарний потенціал як критерій напрямку самовільного перебігу ізобарно-ізотермічного процесу та стану 58 27. 28. 29. 30. 31. 32. 33. 34. 35. рівноваги в закритих термодинамічних системах. Оцінити внесок ентальпійного та ентронійного факторів. Отримати аналітичний вираз фундаментальних рівнянь для відкритих систем в диферепційпій формі з використанням термодинамічних функцій U, H, Р, G та в інтегральній формі для ізобарноізотермічних процесів. Довести, цю хімічний потенціал є функцією стану термодинамічної системи. Обґрунтуйте фізичний зміст хімічного потенціалу. Довести, що зменшення величини хімічного потенціалу термодинамічної системи є кількісним критерієм напрямку самоцільних процесії у відкритих системах. За допомогою якого рівняння можна розрахувати концентрацію компонента пі в будь-який момент перебігу хімічного процесу, якщо відома його початкова концентрація пі,0 та ступінь або глибина перебігу хімічної реакції X? Використовуючи інтегральну форму фундаментального рівняння для відкритого ізобарно-ізотермічного процесу, встановити залежність ізобарного потенціалу термодинамічної системи від величини X. Отримати рівняння, яке є загальною умовою термодинамічної рівноваги. Навести термодинамічне обґрунтування закону діючих мас. Способи виразу констант рівноваги. Встановити взаємозв'язок між ними. Фізичний зміст закону діючих мас. Довести рівняння ізотерми хімічної реакції. Охарактеризувати це рівняння для застосування як кількісної характеристики напрямку самовільного перебігу реакції та стану хімічної рівноваги. Доведення рівняння ізобари хімічної реакції в диференційній та інтегральній формі без урахування залежності теплового ефекту реакції та теплоємності речовин від температури. Термодинамічне обґрунтування універсального принципу зсуву рівноваги ЛеШательє. Доведення рівняння ізобари хімічної реакції в диференційній та інтегральній формі з урахуванням залежності теплового ефекту реакції і теплоємності речовин від температури. 59 2. ФІЗИКО-ХІМІЧНИЙ АНАЛІЗ 2.1. Застосування другого закону термодинаміки до фазових перетворень Гетерогенними називаються системи, які в різних частинах мають різні фізико-хімічні властивості. Такі системи складаються з декількох однорідних частин або гомогенних систем, відділених одна від одної фізичними поверхнями розділу. Однорідні частини гетерогенної системи називають фазами. Фаза — це сукупність гомогенних частин системи, однакових у всіх точках за складом та фізико-хімічними властивостями та розмежованих одна від одної поверхнею розділу. Гетерогенні системи, таким чином, с багатофазними. Наприклад, склянка води з плаваючими кристалами льоду, та газовою фазою у вигляді повітря, що знаходиться над рідиною, с трифазною системою. Всі кристали льоду становлять одну фазу, хоча вони й обмежені один від одного поверхнями розділу, тому що мають однакові термодинамічні властивості (тобто властивості, що однозначно визначаються тиском, температурою і хімічним потенціалом складових частин) та відрізняються від властивостей повітря і води. Кожна з фаз гетерогенної системи може складатися з декількох речовин (наприклад, суміш газів або рідкий розчин). Термодинамічні властивості фази гетерогенної системи визначаються її температурою, тиском, а також концентраціями складових речовин. Речовини, що можуть бути виділені з фази та існувати в індивідуальному стані, називають компонентами (наприклад, у системі NаNО3 + Н20 компонентами с не Nа+, NО3- , Н+, ОH-, що знаходяться в розчині, а NаNО3 та Н2О. У гетерогенних системах можливий перехід речовини з однієї фази в іншу. Наприклад, лід при відповідних умовах може перетворюватися на воду, вода — па пару. Перехід речовини з однієї фази в іншу називають фазовим. Наприклад, до фазових переходів належать: і перетворення, перехід кристалічних модифікацій твердого тіла одна в одну, розчинення твердої речовини. Фазові переходи можуть бути I та II роду. У фазових переходах першого роду зазнає стрибка перша похідна від термодинамічного потенціалу. Тобто змінюються значення ентропії та об'єму. У фазових переходах другого роду стрибка від термодинамічного потенціалу зазнає друга похідна — тобто теплоємність, коефіцієнт об'ємного розширення. 60 Для того щоб описати властивості кожної з фаз системи, не завжди треба знати концентрацію всіх компонентів суміші. А тому, при вивченні гетерогенної рівноваги введено поняття про кількість незалежних компонентів системи. Під числом незалежних компонентів розуміють найменше число компонентів, яке треба задати для опису властивостей кожної фази гетерогенної системи. Розглянемо розрахунок числа незалежних компонентів на прикладах. У системі NаNО3 + H2О для опису властивостей необхідно зазначити кількість NаNО3 і H20 (початкові концентрації Na+, N03- і асоціатів H20 визначаються концентрацією NаNО:3 і H20 та зовнішніми умовами). Отже, дана система складається із двох компонентів. Газова фаза, що складається з N2, H2, NH3 (взятих у довільних кількостях), має три компоненти. Для опису властивостей фази не обов'язково вказувати кількості всіх трьох речовин, тому що їх концентрації пов'язані між собою умовами рівноваги реакції і не можуть довільно змінюватись: Досить вказати кількості лише двох концентрація третього буде визначена за рівнянням: Р 2NH 3 PN 2 PH3 2 де компонентів, а Kp Р — рівноважні значення парціальних тисків компонентів, Кр — константа рівноваги реакції утворення аміаку. Таким чином, система N2, H2, NH3 хоча й містить три компоненти, за кількістю незалежних компонентів є двокомпонентною. Якщо в цій же системі складові частини брати не довільно, а одержати суміш термічною дисоціацією NH3 (не додаючи ззовні Нг та N2), то число незалежних компонентів буде дорівнювати одиниці, тому що крім зазначеної вище умови додається ще одна: PN2 P H 23 Число незалежних компонентів іноді залежить від зовнішніх умов. Так, система, що складається з H2, 02 і H2О, при низьких температурах має 61 три незалежні компоненти. При високих температурах число незалежних компонентів у пій зменшується до двох, тому що концентрації складових частин виявляються зв'язаними умовою рівноваги реакції: 2.2. Загальні умови рівноваги в гетерогенних системах. Правило фаз Гіббса Розглянемо загальні умови рівноваги гетерогенної системи, що складається з р фаз і к компонентів. Будемо вважати, що в кожній з фаз знаходяться всі к компонентів. Для характеристики кожної фази треба задати її температуру, тиск і концентрації компонентів. Всього необхідно задати к - 1 концентрацій, оскільки концентрація останнього компонента при цьому буде відома: якщо концентрація виражається у відсотках, то вона дорівнює 100 k 1 c i якщо в мольних частках, то вона дорівнює 1 k 1 1 Ni . Отже, стан кожної з фаз визначається к - 1 значеннями 1 концентрацій, температурою і тиском. При рівновазі температура у всіх фазах однакова (термічна рівновага). Однаковим повинен бути і тиск (механічна рівновага). Тому для характеристики всієї гетерогенної системи треба задати наступні незалежні змінні: (к — 1) концентрацій компонентів у р фазах, температуру й тиск, тобто загальне число незалежних змінних дорівнює (к - 1) р + 2. Далі слід врахувати, що умова рівноваги між фазами накладає деякі обмеження на довільність зміни величин (к — І) р + 2. Знайдемо число рівнянь що зв'язують змінні величини. Умовою рівноваги в гетерогенній системі є рівність хімічного потенціалу кожного з компонентів у всіх фазах: 62 де нижній індекс відноситься до номера компонента, а верхній — до номера фази. Кожна рівність тину 11 12 тощо, дає одне рівняння, що зв'язує змінні, які характеризують гетерогенну систему. Всього буде (р — 1) к таких рівнянь (к рядів, у кожному з яких р — 1 рівнянь). Число рівнянь, що зв'язують змінні, не може бути більше числа змінних (інакше система рівнянь буде несумісною). Тому: (p-1) k ≤ (k-1) p + 2 (2.1) Якщо число рівнянь k (р — 1) дорівнює числу невідомих (k — 1) р + 2, то система рівнянь має однозначне рішення. Це значить, що рівновага в гетерогенній системі можлива лише при чітко фіксованих значеннях всіх її параметрів (температури, тиску й концентрацій кожного компонента у всіх фазах). Якщо ж k (р - 1) < (k -1) k + 2, то кількість фаз системи може не порушуватися" при зміні однієї чи декількох змінних. Різниця між числом невідомих і числом рівнянь, що їх об'єднують, показує кількість змінних, які можна одночасно змінювати, не викликаючи зникнення або виникнення нових фаз у системі. Цю величину називають числом ступенів вільності системи С. Таким чином, числом ступенів вільності називається число змінних (температура, тиск і концентрації компонентів), які можна незалежно та одночасно змінювати, не викликаючи зникнення або виникнення нових фаз. Відповідно до викладеного вище (2.2) де (2.3) Число ступенів вільності гетерогенної системи дорівнює числу компонентів плюс два, мінус число рівноважних фаз у системі. Це співвідношення називають основним законом фазової рівноваги, або рівнянням Гіббса. Воно було одержано американським фізиком Дж. Гіббсом 1876 року. Кількість ступенів цільності характеризує варіантність системи, тобто 63 кількість незалежних змінних (тиск, температура, концентрація компонентів), які можна в певних межах змінювати так, щоб кількість і природа фаз у системі не змінювались. За кількістю фаз системи поділяють на одно -, двофазні та інші, за кількістю компонентів — одно-, дво-, трикомпонентні, за кількістю ступенів вільності — на нонваріантні (безваріантні, С = 0), моноваріантні (С = 1), диваріантні (С = 2) тощо. Якщо на рівновагу системи, крім температури і тиску, впливають інші зовнішні фактори, наприклад, електричне або магнітне поле, зміна рН середовища, то в рівнянні (1.3) кількість зовнішніх факторів перевищуватиме два; визначимо їх через n і тоді (2.4) 2.3. Фазові рівноваги в однокомпонентних 2.3.1. Рівняння Клаузіуса-Клайперона Розглянемо фазові переходи першого роду в однокомпонентних системах. Основною характеристикою фазових перетворень с температура, при якій фази перебувають в стані рівноваги. Вона залежить від тиску. Фазові переходи відбуваються зворотно при незмінних температурі і тиску, тому термодинамічні потенціали фаз, що перебувають у стані рівноваги, однакові Нехай рідина перебуває в етапі рівноваги зі своєю парою при температурі Т і тиску Р. Термодинамічним критерієм рівноваги при Т = соnst і Р = соnst є рівність ізобарних потенціалів обох фаз Для того щоб дві фази залишились у стані рівноваги при збільшенні температури до Т + dТ, тиск мас зрости до Р +dР. Ізобарний потенціал також зміниться для рідини до Gрід + dGрід для пари — до Gn + dGn. Рівновага встановлюється при умові: оскільки 64 Звідки отримуємо: або з рівняння де L – теплова фазового перетворення (2.5) Це рівняння називають рівнянням Клаузіуса-Клапейрона; воно пов'язує тиск і температуру і справджується для будь-якого фазового переходу першого роду. Для процесів випаровування і сублімації рівняння (2.5) можна подати в іншому вигляді. Об'єм рідини дуже малий порівняно з об'ємом пари Vn >>Vрід тому об'ємом рідини можна знехтувати: Вважаючи, що для пари можна застосувати рівняння ,стару ідеального газу, дістанемо Підставляючи замість Vn його значення в (2.5), отримуємо або (2.6) Це рівняння Клаузіуса-Клапейрона для процесу випаровування рідин. Оскільки L, Р, Т завжди є додатними величинами, то похідна також 65 завжди є додатною. Отже, зі зростанням температури тиск насиченої пари над рідиною завжди збільшується. Цей висновок має велике практичне значення при проектуванні парових котлів, автоклавів, вакуум-апаратів та іншого обладнання для харчової промисловості. Після інтегрування ( 2 . 6 ) в межах від Р 1 до Р 2 та від Т 1 до Т 2 за умови, що L не змінюється в даному інтервалі температур, отримуємо: (2.7) При інтегруванні (2.6) у широкому інтервалі температур необхідно величину L виразити як функцію від неї. Для процесу плавлення ( 2.5 ) запишемо таким чином (2.8) Знак похідної -- dT залежить dP від знаку зміни об’єму при плавленні. dT 0 , тобто зі зростанням dP тиску температура плавлення підвищиться. Якщо V 0 , то зі зростанням Якщо V 0 та Vрозплав> Vтв.фаза , то тиску температура плавлення знижується. Така властивість притаманна невеликій кількості речовин: воді, вісмуту, галію, деяким маркам чавуну. 2.3.2. Діаграми стану води та сірки Найпростіші гетерогенні системи складаються з одного компонента к = 1. До них належать всі індивідуальні речовини. Відповідно до правила фаз Гіббса (2 .3 ) , для однокомпонентних систем С = 3 - р. (2.9) Отже, в однокомпонентних системах одночасно в рівновазі може перебувати не більш трьох фаз (р 3), тому що ступінь вільності С не може бути від'ємною величиною. Якщо для однокомпонентної системи С 2, то число фаз не може бути менше 1. Такі системи називаються біваріантними. У них можна одночасно змінювати дві змінні (температуру й 66 тиск), не викликаючи при ньому виникнення нової фази. Так, у визначених межах можна незалежно змінювати тиск і температуру рідини, твердого тіла чи пари, не викликаючи фазових переходів (наприклад, вода може існувати у відомому інтервалі температур і тисків). Однакпри зміні температури чи тиску понад визначеної межі відбувається фазовий перехід (плавлення, випаровування тощо) і утворюється друга фаза (р = 2 ) . Тоді, відповідно до правила фаз. С = 3 — 2 = 1. Такі системи називаються моноваріантними. У них можна змінювати або тільки тиск, або температуру, не змінюючи числа фаз. Таким чином, кожному значенню температури в однокомпонентній двофазній системі відповідає єдине значення тиску, при якому фази знаходяться в рівновазі. Однокомпонентні системи характеризуються лише двома незалежними змінними — температурою й тиском (поняття про концентрацію для індивідуальних тіл позбавлено змісту). Властивості подібних систем за різних зовнішніх умов можна графічно зображувати на площині, відкладаючи по одній з координатних осей — абсцисі — температуру, а по другій — ординаті — рівноважний тиск. Такі діаграми називають фазовими діаграмами стану однокомпонентних систем. Рис. 2.1. Фазова діаграма стану води Розглянемо для прикладу плоску діаграму стану води при невисоких тисках (рис. 2.1). Лінія оа зображує залежність тиску насиченої пари води від температури, лінія оb передає залежність тиску насиченої пари льоду від температури (співіснуван н я льо д у і пар и) , а лі нія ос — залежність 67 температури плавлення льоду від тиску. Зі збільшенням тиску температура плавлення льоду зменшується (крива спрямована вліво). Для більшості ж інших речовин — навпаки, тобто при збільшенні тиску температура плавлення підвищується (крива нахилена вправо). Це залежить від знаку похідної у рівнянні Клаузіуса —Клапейрона для даного процесу dp L , v1iv2 - мольні об’єми у твердому і рідкому dT (v2 v1 ) станах. Для води v 2 — v1 < 0, і тому більшості випадків v2 — v1 > 0 і dp 0 (крива нахилена вліво). У dT dp 0 dT Площа І (рис. 2.1) характеризує область існування твердого льо ду, П — рідкої води і III— пари. Розглянемо, наприклад, систему, що характеризується тонкою x1 яка відповідає стану твердого льоду. При зниженні тиску (якщо t = сопst) до точки х 2 фазових переходів не буде (стійкою залишається тверда фаза). У точці х2 система стає двофазною (рівновага лід-нар). Якщо ще зменшувати тиск, лід зникає, і в точці х3 буде тільки одна ненасичена пара. Аналогічно при підвищенні температури при постійному тиску від х1 до х4 зберігається лід; у точці х4 спостерігається рівновага лід-вода. Подальше підвищення температури призводить до зникнення льоду. У точці х 5 існує тільки рідина. Якщо зменшувати її тиск при постійній температурі, то до точки х6 буде залишатися тільки фаза рідини; у точці х 6 виникає фазова рівновага вода-пара. Подальше зменшення тиску призводить до зникнення рідини, і в х 7 буде вже ненасичена пара. Крива оа переривається в точці а, що відповідає критичній температурі tкр. В цій точці зникає різниця між властивостями рідини та її пари, тобто досягається критичний стан. Критичний етап — це стан, в якому дві або більша кількість фаз речовини, які перебувають між собою у стані термодинамічної рівноваги, стають тотожними за своїми властивостями. Всі три криві оа, оb і ос перетинаються в одній точці о, що називається потрійною. У цій точці одночасно знаходяться в рівновазі три фази: лід, вода й пара. Відповідно до правила фаз Гіббса р = 3 і С = 0. Такі системи називають нонваріантними. Це означає, що в них не 68 можна змінювати ні тиск, ні температуру, не викликаючи при цьому зникнення якої-небудь фази. Три фази води існують при чітко визначених тиску і температурі, Р = 60,8814 Па (0,457 мм рт. ст.) і Т = 0.0076 0 С. Крива оа може бути продовжена в область «льоду», ділянка оd відповідає існуванню переохолодженої води в рівновазі з парою. Тиск насиченої пари переохолодженої води вищий, ніж у льоду. Переохолоджена вода нестійка і при незначних зовнішніх впливах переходить у лід. Діаграми стану однокомпонентних систем ускладнюються, якщо у твердому етапі дана речовина має поліморфні модифікації. Як приклад на рис. 2.2 наведена діаграма стану сірки, що має дві модифікації (ромбічну й моноклинну). Крива аb характеризує залежність тиску насиченої нари ромбічної сірки від температури, криві bс і сd — аналогічну залежність для моноклинної й рідини. Лінія bе показує залежність температури перетворення ромбічної сірки в моноклинну [S(р)S(м)] від тиску; лінія се — залежність температури плавлення S(м) від тиску та еg; — залежність температури плавлення S(ромб.) від тиску. Область S(ромб.) — Рис. 2.2. Фазова діаграма стану сірки облаcть існування ромбічної сірки, S(м) — моноклинної S(р) — рідкої та S(пара) — газоподібної. На діаграмі с три потрійні точки: b відповідає рівновазі між S(р), S(м) і S(пара), с — рівновазі м і ж S ( м ) , S ( п а р а ) т а S ( р ) і с — рівновазі між S(р), S(м) і S(рідина). Слід враховувати, що всі 69 модифікації можуть знаходитися в метастабільних станах. Так, bс' — метастабільний стан S(м), bb' — метастабільний етап S(ромб.), сb' — переохолоджена рідка сірка. 2.3.3. Характеристика поліморфних перетворень. Діаграма стану фосфору Поліморфні перетворення твердих тіл бувають двох типів: зворотні та незворотні. Якщо перетворення зворотні, то за певних зовнішніх умов модифікація І переходить у модифікацію II, а за інших умов, навпаки, друга модифікація самовільно переходить у першу. Таким чином, в одному температурному інтервалі більш стійкою с перша, а в іншому інтервалі температур — друга поліморфна модифікація. Такі поліморфні перетворення називають енантіотропними. Це перетворення ромбічної сірки в моноклинну, червоної модифікації Hg2 — у жовту, поліморфні перетворення льоду та інші. Так, при t > 95,5 0С стінкою є моноклинна сірка, а при t < 95,5°С — ромбічна. У природі часто одна з поліморфних модифікацій у всьому температурному інтервалі свого існування с: нестійкою, а інша — стійкою. Тоді модифікації можуть перетворюватися тільки в одному напрямку (із нестійкої у стійку форму). Такі переходи називають монотронними. Для з'ясування причин енантіотронії та монотропії необхідно врахувати наступне: - стійкою за даних умов с та модифікація, тиск насиченої пари якої найменший: - тверде тіло неможливо перегріти, тобто при температурі, коли тиск насиченої нари рідини стає менший за тиск пари твердого тіла, останнє плавиться; - поліморфні модифікації можуть існувати в метастабільному стані (можуть бути перегрітими вище температури перетворення в іншу модифікацію чи переохолодженими нижче неї). Легко показати, що характер поліморфного перетворення залежить від того, при яких температурах крива тиску насиченої пари рідкої фази перепинає криві тиску парів кристалічних модифікацій. Якщо ця температура лежить вище температури переходу кристалічних модифікацій, то їхнє перетворення є енантіотропним (може самовільно відбуватися в обох напрямках) і, навпаки, якщо точка перетину кривої тиску пари 70 рідний із кривими тиску насичених парів кристалічних модифікацій лежить нижче їх температури переходу, то перетворення буде монотропним (тобто можливий самовільний перехід лише в одному напрямку). На рис. 2.3 схематично зображено діаграму стану системи, у якій можливо енантіотропне перетворення. Крива abb' характеризує залежність тиску насиченої пари модифікації II від температури (bb' — ділянка метастабільного стану), крива с'bс— те саме для модифікації І (с'b — метастабільна ділянка). При Т < Тп стійка модифікація II (р 2 < р 1), при Т > Тn стійка модифікація 1 (Р 1 < Р 2 ). Крива а'b'сd — залежність тиску насиченої пари рідкої фази від температури (ділянка (a'b'с — переохолоджена рідина), сg — крива залежності температури плавлення модифікації І від тиску, крива b ’ h — залежність температури плавлення метастабільної модифікації II від тиску та bе — залежність температури переходу І II від тиску. У подібних системах при Т < Тп спостерігається спонтанний перехід І II, а при T > Tn навпаки, II І. Рис. 2.3. Діаграма стану однокомпонентної системи, у якій відбуваються енантіотропне перетворення кристалічних модифікацій Звичайно, із метастабільного стану не відразу утвориться найбільш стійка за даних умов модифікація. Найчастіше спочатку виникає найближча до тиску насиченої пари, більш стінка, хоча теж метастабільна модифікація, що далі переходить у найбільш стійку. Ця закономірність називається правилом ступенів Освальда. Нехай рідка фаза переохолоджена до Т1 (рис. 2.3, точка К1), тоді з неї відразу утвориться стійка при цих умовах модифікація І. Якщо ж її охолодити до Т2, (К2), то спочатку утвориться метастабільна модифікація II (найближча за тиском пари), а далі вона перейде в стійку модифікацію І. Якщо переохолодити рідину до Т3 (К3), то, 71 навпаки, утвориться метастабільна модифікація І, що потім переходить у другу. Інші закономірності характерні для систем, у яких відбуваються монотропні перетворення. На рис. 2.4 наведена діаграма стану такої системи. Крива аbb' передає залежність тиску насиченої пари модифікації І від температури (ділянка bb' нездійсненна, тому що вона відповідає твердому тілу, перегрітому вище температури плавлення). Крива сdd' — це те саме для модифікації II (ділянка dd' також нездійсненна). При всіх температурах аж до температури плавлення стійкою с модифікація І (р 1 < p 2). Ці модифікації взаємно перетворювалися б лише при Т > Тп (коли р 2 < p 1 ) , але це неможливо, тому що температура переходу Тn лежить вище температури плавлення обох модифікацій, тобто при Т n вони не існують у кристалічному стані. Рис. 2.4. Діаграма стану однокомпонентної системи монотропними перетвореннями кристалічних модифікацій Рис. 2.5. Діаграма стану фосфору 72 У подібних системах можливий тільки самовільний перехід II 1 (але не навпаки). Якщо переохолодити рідину до Т 1, то при кристалізації утвориться стійка форма. При охолодженні ж до Т2 спочатку утвориться метастабільна модифікація II (найближча форма), що далі перетворюється в І. Така діаграма стану характерна, наприклад, для фосфору (рис. 2.5). Крива gh — залежність тиску насиченої пари стійкої фіолетової модифікації від температури, к'hк— те саме для рідкого фосфору (к'h — ділянка переохолодженої рідини), hк — залежність температури плавлення фіолетового фосфору під тиску. Точка h — потрійна точка — істинна рівновага твердого фіолетового фосфору (область існування I+ II + III), рідкого фосфору (область IV) і пари (область V). Криві аb і bс залежності тиску насичених парів нестійких алотропних модифікацій (фосфор білий II і фосфор білий І); b— точка переходу нестійкого білого фосфору II у білий фосфор І, bb' — залежність температури цього переходу від тиску, се — залежність температури плавлення нестійкого білого фосфору І від тиску. 2.4. Фазові рівноваги у двокомпонентних системах 2.4.1. Основи фізико-хімічного аналізу Багатокомпонентні системи з кількома рівноважними фазами вивчають за допомогою фізико-хімічного аналізу, тобто досліджують залежність будьякої фізико-хімічної властивості (в'язкості, густини, електропровідності, температури, тиску тощо) від складу системи. За дослідними даними будують діаграму стану властивість-склад. Для двокомпонентних систем властивість відкладають на осі ординат, а склад — на осі абсцис. При вивченні діаграм стану можна встановити характер взаємодії компонентів системи, умови утворення хімічних сполук, їх склад, температуру плавлення тощо. Фізико-хімічний аналіз ґрунтується на принципах безперервності і відповідності. Згідно з принципом безперервності при постійній зміні параметрів, які визначають стан системи (тиск, температура тощо), властивості її окремих фаз змінюються також постійно доти, доки не зміниться кількість і характер її фаз. Коли з'являються нові або зникають існуючі фали, властивості системи змінюються стрибкоподібно. Згідно з принципом відповідності кожній фазі або кожному комплексу рівноважних фаз па діаграмі відповідає певна геометрична фігура. 73 Фізико-хімічний аналіз широко застосовують при вивченні гетерогенних систем у харчовій промисловості: перегонці рідких сумішей, кристалізації цукру тощо. Одним з видів фізико-хімічного аналізу є термічний, за допомогою якого можна побудувати діаграму етапу (діаграму плавлення) за кривими охолодження. Для цього необхідно визначити температури плавлення сумішей компонентів при всіх можливих співвідношеннях. У деяких випадках температуру плавлення можна визначити візуально, фіксуючи за термометром температуру, при якій починається виділення перших кристалів твердої фази, або температуру, при якій останні кристали твердої фази плавляться. Найбільш загальним методом визначення температури плавлення сумішей є метод термічного аналізу, заснований па вивченні кінетики охолодження розплавів. Цей метод найбільш досконало розкритий у працях М.С. Курнакова, який сконструював прилад (пірометр Курнакова), що дозволяє автоматично записувати диференціальні крипі охолодження. Характер кривих охолодження показаний на рис. 2.6. Крива І на цьому рисунку відповідає охолодженню індивідуальної речовини. Якщо охолоджувати розплав індивідуальної речовини, його температура знижується практично з постійною швидкістю (лінійна ділянка аb) до температури плавлення, коли з розплаву починають випадати кристали твердої фази. Рис. 2.6. Криві охолодження Цей процес супроводжується виділенням теплоти (прихована теплота плавлення). Для індивідуальної речовини він відбувається при постійній 74 температурі. Тому до того моменту, доки весь зразок не викристалізується, температура залишається постійною (ділянка bс). Потім температура твердої фази, що утворилася, знову починає зменшуватися з часом практично лінійно (сd). Ділянка bс. паралельна осі часу, характеризує температуру плавлення речовини. Трохи складніші криві охолодження суміші (крива II). У цьому випадку до початку кристалізації температура також знижується з часом практично лінійно (а'b'). Однак суміш на відміну від індивідуальної речовини кристалізується не при постійній температурі, хоча процес також є екзотермічним. Це зумовлено тим, що при виділенні кристалів одного з компонентів суміш збагачується другим, і температура. Ті кристалізації знижується. Тому на кривих охолодженння при температурі початку кристалізації (точка b') відбувається лише злам кривої, і швидкість охолодження зменшується внаслідок виділення теплоти (ділянка b'с' ). Температура падає доти, доки склад сплаву не стане евтектичним (точка с'). З цього моменту сплав буде кристалізуватися при постійній температурі (ділянка с'd'). У точці d’ сплав цілком викристалізовується і тоді починається охолодження твердої фази (d'c’). Що ближче склад сплаву до евтектичного, то менше ділянка b'с' і то більше ділянка с'd’. Для евтектичного сплаву крива охолодження (III) має такий самий вигляд, як для індивідуальної речовини. При побудові діаграми стану слід враховувати температуру, при якій відбувається злом кривої Т = f( ), тобто точку b ’, що відповідає початку кристалізації. Одним із практично важливих прикладів розглянутих двокомпонентних сумішей є розчини твердих речовин у воді чи інших розчин пиках. На рис. 2.7 показана діаграма стану водних розчинів СrO3. У цій системі є евтектична точка, яку для водяних розчинів називають кріогідратною. Розчин даної речовини у воді, що мас найбільш низьку температуру замерзання, називають кріогідратом. Кріогідрат являє собою евтектику, при замерзанні якої утвориться суміш дрібних кристаликів льоду і розчиненої речовини. Кріогідратні точки для різних речовин лежать при різних температурах. Так, для NаCl вона дорівнює 21,2, для ZпСl2 — 62 і для СrО3 — 105 °С. Кріогідрати використовуються на практиці для одержання охолоджувальних сумішей (як джерела постійних низьких температур). Для одержання кріогідратів змішують лід і дану тверду сполуку. У результаті розчинення цієї сполуки у воді лід частково плавиться, що супроводжується 75 поглинанням теплоти (прихована теплота плавлення), і температура суміші знижується до кріогідратної. Рис. 2.7. Діаграма стану системи Н2O – CrO3 Для них систем можна побудувати діаграми стану, аналогічні до сплавів. Різниця полягає лише в тім, що температура плавлення солі зазвичай, вища за критичну температуру розчинника, і тому неможливо вивчати розчини води (чи іншого розчинника) у розплавленій солі. Подібні діаграми етапу не можна довести до кіпця, що відповідає чистому твердому компоненту. В усьому іншому вони мають такий самий вигляд, як і для сплавів. Діаграми етапу багатьох двокомпонентних систем можуть бути значно складніші, ніж розглянуті вище. Це зумовлено низкою чинників: утворенням хімічних сполук між компонентами суміші, частковим чи безмежним змішуванням речовий у твердому стані, можливістю поліморфних перетворень у твердих фазах і обмеженою взаємною розчинністю в рідкому стані. Ці ускладнені діаграми стану будуть розглянуті далі. 2.4.2. Діаграми стану двокомпонентних систем з евтектикою Всі фазові діаграми стану двокомпонентних систем можна класифікувати на 5 типів: діаграми стану двокомпонентних систем з евтектикою, діаграми стану двокомпонентних систем, в яких утворюються конгруентно та інконгруентно плавкі хімічні сполуки, діаграми стану систем, в яких утворюються неперервні та обмежені ряди твердих розчинів. Відповідно до правила фаз Гіббса для двокомпонентних систем С 76 = 4 - р. Це свідчить про те, що у двокомпонентній системі одночасно може співіснувати не більше Чотирьох фаз — нонваріантна система (четверна точка). Двокомпонентні системи, що містять три фази — моноваріантні і т.д. Максимальне число ступенів вільності (при р = 1) для двокомпонентної системи дорівнює трьом, тобто вони триваріантні. Не порушуючи фазності в таких системах, у певних межах можна незалежно змінювати температуру, тиск і склад. Кожна фаза двокомпонентної системи характеризується трьома змінними: температурою, тиском і концентрацією одного з компонентів. Тому для побудови діаграми стану двокомпонентних сумішей необхідно використовувати просторову систему координат. Просторові діаграми стану недостатньо наочні. їх побудова пов'язана зі складнощами, і тому ними практично не користуються. Найчастіше при побудові діаграм етапу двокомпонентних систем розглядають рівновагу тільки в конденсованих фазах, що значно спрощує завдання. Дійсно, якщо обмежитися розглядом властивостей системи при постійному тиску і вибрати цей тиск більшим, ніж тиск насичених парів сумішей будь-якого складу (звичайний тиск приймають за 1,0133 10 +5 Па (1 атм). то в системі газоподібної фази не буде. Тим самим обмежуються розглядом умови рівноваги в рідких і твердих фазах. При цьому зміниться і форма запису правила фаз. Число ступенів вільності (варіантність) при постійному тиску зменшується на одиницю, і його можна назвати умовною варіантністю системи. Умовну варіантність двокомпонентної системи можна розрахувати за рівнянням С = 3 — р. Використовуючи цей метод, будують площинні діаграми етапу двокомпонентних систем у координатах Т =f(склад). Найбільш прості .діаграми стану систем, у яких компоненти необмежено змішуються в рідкому етапі, зовсім не змішуються у твердому і хімічно не взаємодіють один з одним. У таких системах, що являють собою молекулярні суміші, можуть співіснувати розплави — фаза змінного складу із кристалами окремих компонентів. На рис. 2.8 схематично зображена діаграма етапу подібної системи. На відрізку осі абсцис dg відкладений склад системи (виражений у мольних частках компонентів чи в інших відносних концентраційних одиницях), по осі ординат — температура. Нехай точки t1 і t2 відповідають температурам плавлення першого й другого компонентів в індивідуальному стані. Якщо компоненти не змішуються у твердому стані, тобто не утворюють 77 твердих розчинів, додавання другого компонента до першого (його можна розглядати як розчинник) завжди призводить до зменшення температури плавлення. Залежність температури початку кристалізації суміші від складу другого компонента схематично зображується відрізком кривої t1е. Аналогічно, якщо додавати пертий компонент до другого (розчинника), то температура початку кристалізації також буде зменшуватися (відрізок t2h). Відрізки t1е і t2h спрямовані назустріч один одному і перетинаються в деякій точці а. Ця точка називається евтектичною, а відповідна їй суміш — евтектикою. Евтектика мас найбільш низьку температуру плавлення з усіх можливих сумішей даних компонентів. Розглянемо процес кристалізації сплаву довільного складу, наприклад, що відповідає точці k (рис. 2.8). У цій точці, що відповідає рідкому розплаву, є тільки одна фаза, і тому С = 3 — 1 = 2, тобто система біваріантна. У ній можна довільно змінювати температуру і склад, не змінюючи числа фаз. При охолодженні суміші до точки є (до температури її плавлення) із суміші починає виділятися тверда фаза, що складається із кристалів компонента І. У точці є система стане двофазною і буде складатися з рідкого розплаву та кристалів компонента І. Умовна варіантність С дорівнюватиме одиниці. Отже, при зміні температури буде змінюватися і склад розплаву. При виділенні з розплаву кристалів компонента І розплав збагачується другим компонентом, і температура початку його кристалізації буде знижуватися (ділянка кривої еа). Аналогічно, якщо охолоджувати розплав, склад якого відповідає точці І, до точки h система залишається однофазною, і її варіантність дорівнює дном. У точці h з розплаву починають виділятися кристали компонента Рис. 2.8. Діаграма стану двокомпонентних систем евтектичного типу 78 ІІ, розплав буде збагачуватися компонентом І, і температура початку його кристалізації буде знижуватися (ділянка hа). Так триватиме доти, доки розплав не досягне евтектичної точки. При кристалізації евтектики одночасно виділяються пристали обох компонентів, у тому ж співвідношенні, у якому вони знаходяться в розплаві. Таким чином, у точці а система складається з трьох фаз (розплав, кристали компонента І і кристали компонента I I ) , і тому вона нонваріантна. Це означає, що евтектична суміш мас постійний склад і постійну температуру кристалізації. За такими властивостями евтектика нагадує хімічну сполуку — характеризується сталим складом та сталою температурою плавлення. Деякі дослідники припускали, що рідка евтектика дійсно є неміцною хімічною сполукою компонентів. Проте це невірно, тому що склад евтектики залежить від зовнішнього тиску. Евтектика кристалізується при певній постійній температурі й у твердому стані складається з рівномірно розподілених дрібних кристалів обох компонентів. Діаграми стану системи дозволяють описувати її властивості при різних температурах. Ділянка над кривою t1еahl2 — це область існування рідких розплавів. Тут система однофазна, і її варіантність дорівнює двом. Сама лінія t1еahl2 що називається лінією ліквідуса, характеризує температуру початку кристалізації сплавів різного складу. Заштрихована площа t1eас являє собою гетерогенну область, у якій суміш розділяється на тверду фазу (кристали І) і розплав визначеного складу. Так, у точці т співіснують кристали компонента І (точка р) та розплав складу о. Точки о та р, що характеризують склади співіснуючих фаз, називаються спряженими. Кількості розплаву і твердої фази можуть бути знайдені за допомогою правила важеля, яке можна застосувати в усіх випадках, коли в стані рівноваги перебувають дві фази. Правило важеля стверджує, що фігуративна точка m поділяє конноду (ноду) ро на 2 відрізки, відношення яких дорівнює зворотному відношенню мас рівноважних фаз: маса _ кристалів то маса _ розплаву тр Прямі, що з'єднують точки, які характеризують склади співіснуючих фаз, називаються нодами. У розглянутих системах вони паралельні осі абсцис. Аналогічно площа t2hаb також відповідає гетерогенній області, у 79 якій сплави розділяються па кристали компонента II і розплав. Так, сплав, склад якого відповідає точці q, при температурі tq розділяється на кристали компонента II і розплав (точка п). Нижче прямої саb, що називається лінією солідуса, сплави перебувають винятково у твердому етапі. В області саrd система складається із кристалів компонента І і евтектики, яка сама є тонкою сумішшю кристалів обох компонентів. Область bаrg — це суміш кристалів компонента II і евтектики, тобто суміш кристалів двох компонентів. 2.4.3. Діаграми стану двокомпонентних систем,в яких утворюються конгруентно та інконгруентно плавкі хімічні сполуки Компоненти суміші часто хімічно взаємодіють один з одним. Сполуки, що утворюються, можуть бути настільки міцними, що вони існують як у твердому, так і в рідкому стані, тобто плавляться без розкладання. Такі сполуки називаються конгруентно плавкими. Особливості діаграм стану систем, в яких утворюються конгруентно плавкі сполуки, неважко теоретично передбачити. Нехай у системі, що складається з компонентів А і Б, утворюється міцна хімічна сполука складу An Вm Припустимо далі, що речовими А, В і An Вm необмежено змішуються в рідкому стані і зовсім не змішуються у твердому. Діаграма стану такої системи повинна мати вигляд, зображений на рис. 2.9. На цьому рисунку точки T A, T B і с відповідають температурам плавлення компонентів A і B і їх хімічної сполуки An Вm. Якщо до компонента А додавати хімічну сполуку, температура плавлення суміші зменшується (відрізок ТAа). Якщо взяти речовину An Вm і до неї додавати компонент A, то температура плавлення буде також знижуватися (підрізок сd). Лінії ТAа і cd спрямовані назустріч одна одній і при продовженні перетинаються в точці 6. Аналогічні криві можна одержати, додаючи компонент В до An Вm та навпаки, An Вm — до компонента В. Таким чином, на діаграмах стану бінарних систем, в яких утворюється конгруентно плавка сполука, мас спостерігатися один максимум (точка с ) , що відповідає температурі плавлення речовини An Вm і дві евтектичні точки b та f. ТA bсfTB — лінія ліквідуса, hbikfl — лінія солідуса. Між цими лініями знаходяться гетерогенні області, у яких суміші розділяються па рідкий розплав і кристали одного з компонентів. 80 Рис. 2.9. Діаграма стану двокомпонентної системи, у якій утворюється конгруентно плавка сполука Розглянемо фазові перетворення які спостерігаються при охолоджені суміші, що відповідає точці х, (рис. 2 . 9 ) . У цій точці суміш однофазна, і тому система біваріантна, тобто можна одночасно змінювати склад і температуру, не викликаючи зміни числа фаз. У точці х2 система стає двокомпонентною (рідкий розплав і кристали А ) , і тому вона моноваріантна. У гетерогенній області ТАаbh суміш розпадається па розплав і кристали А. Так, у точці х3 утвориться розплав складу а і кристали компонента А (при даній температурі). Точка b є евтектичною. Ця евтектика (перша) складається з дрібних кристалів А та AnBm У точці b суміш нонваріантна (р = З, С = 3 - 3 = 0). Площа І (нижче лінії соліду са) складається із суміші кристалів А та першої евтектики. Точка с відповідає чистій хімічній сполуці, тобто в пій система має тільки один компонент (к = 1 і р = 2). Тому вона нонваріантна (так само, як і в точках Т А і ТВ ). У гетерогенній області сdbi суміш розшаровується на розплав і кристали AnBm В області II (нижче лінії солідуса) суміш складається з кристалів AnBm і першої евтектики. Аналогічно, в області сkf суміш розділяється па кристали AnBm і розплав. Точка f — друга евтектика (суміш AnBm і В). На ділянці III (нижче лінії солідуса) суміш складається з АпВт і другої евтектики, а на ділянці IV — із кристалів В та другої евтектики. Таким чином, па діаграмах стану бінарних систем при наявності в них однієї хімічної сполуки, що плавиться конгруентно, спостерігається гострий максимум на кривій ліквідусу, положення якого чітко відповідає складу з'єднання, що утворюється. Цю концентрацію М.С. Курнаков назвав сингулярною, або дальтонівською. Ордината дальтонівської точки відповідає температурі плавлення хімічної сполуки, що утворюється в суміші. 81 Діаграму стану розглянутого тину можна отримати тільки тоді, коли хімічні сполуки при плавленні не розкладаються. Але такі системи трапляються досить рідко. Найчастіше хімічна сполука при плавленні більшою чи меншою мірою дисоціює за рівнянням: AnBm nA mB Дисоціація AnBm призводить до того, що максимум па кривій плавкості (точка с на рис. 2.9) розмивається. Що дужче дисоціює AnBm, то більше розмитий максимум на кривій ліквідусу. Це пояснюється тим, що в точці с знаходиться не індивідуальна речовина, а суміш AnBm, А і В. Діаграми етапу систем, в яких утворяться хімічні сполуки, стійкі тільки у твердому етапі, мають інший вигляд. Такі сполуки, названі інконгруентно плавкими, вище певної температури розкладаються, утворюючи розплав і кристали одного з компонентів. При цьому склад рідкої і твердої фаз не збігаються. На рис. 2.10 схематично зображена діаграма стану системи, у якій утворюється інконгруентно плавка сполука ( AnBm). В таких системах Рис. 2.10. Діаграма стану двокомпонентної утворюється інконгруентно планка сполука системи, у якій на кривій ліквідусу ТАbсТB є точка перетину с, названа перехідною, або перитектичною точкою. Починаючи від цієї точки лінія ліквідусу мало би 82 підніматись по кривій сd (штрихи), але при цій температурі T1, сполука AnBm розкладається, утворюючи розплав і кристали компонента В. Надалі па ділянці сТв виділяються кристали В. Перитектична точка не збігається зі складом AnBm (цей склад визначається точкою є, що відповідає максимуму на експериментально нездійсненній ділянці кривої сdd'). Діаграму на рис. 2.10 неважко розшифрувати, як і всі попередні. Так, ТAbк — це гетерогенна область, у якій суміші розділяються на A і розплав. Ділянка сТBТ1 — гетерогенна область: суміші розшаровуються на В і розплав. На підрізку лінії ліквідусу сb починається виділення з розплаву хімічної сполуки AnBm. Область І — розплави. Область II — тверді суміші Л і евтектики (топка суміш А та AnBm). Область III — тверді суміші AnBm і евтектики. Область IV — В і AnBm. Якщо охолоджувати суміш, що відповідає точці f, то до перетину з кривою сТB буде одна фаза (рідкий розплав) і система залишається біваріантною. Нижче лінії сТВ суміш розділяється на розплав і кристали компонента В. У цій області система моноваріантна. У точці F (при температурі T1) починає утворюватися AnBm і в рівноважній суміші знаходяться три фази (розплав складу с, AnBm і В), тому в точці с система нонваріантна так само, як у евтектичних і сингулярних точках. Співвідношення між кількістю кристалів В, що випадають (точка F), і сполуки, що утворюється (точка с) , визначається за правилом важеля. Якщо далі знижувати температуру, утвориться хімічна сполука AnBm. Цей процес призводить до витрати кристалів компонента В, тому що вихідна суміш f містила деякий надлишок компонента A порівняно зі складом сполуки AnBm,, що утвориться. Тому реакція утворення цієї сполуки закінчиться тоді, коли буде використаний весь компонент В. Після цього залишається надлишок А і тому в області III буде А, та евтектика. Аналогічно можна розглянути процеси, що супроводжують охолодження сумішей, які відповідають точкам g і h. Якщо охолоджувати розплав, що відповідає складу AnBm (точка g), на лінії сТв починається виділення В, у точці d" суміш розшаровується на розплав, що відповідає точці с, і кристали В. Нижче цієї точки утворюється AnBm, а кристали компонента В, що нипали, витрачаються. По лінії d"е система являє собою кристали AnBm. Аналогічно склад суміші, що відповідає точці h,. по закінченні охолодження відповідатиме сполукам AnBm і В (ділянка IV). 83 2.4.4. Діаграми стану двокомпонентних систем, у яких співіснують фази змінного складу До таких систем належать, наприклад, бінарні суміші рідин, які обмежено розчиняються одна в одній і розшаровуються па дві співіснуючі фази, а також суміші, що складаються з бінарного розчину, який знаходиться в рівновазі з насиченою парою. Рис. 2.11. Діаграма стану сумішей рідин, що обмежено розчинні іодна в одній На рис. 2.11 наведена схематична діаграма стану системи, що складається з двох рідин, які обмежено змішуються, з верхньою критичною температурою розшарування. Заштрихована ділянка (асb) — гетерогенна область, у якій суміші розділяються па два співіснуючі шари. Щоб розрахувати число ступенів вільності системи при різних умовах, необхідно врахувати, що при побудові діаграми тиск приймали постійним і більшим за тиск насиченої пари суміші у всьому інтервалі температур, який наведено на діаграмі. За такої умови існують тільки сконденсовані, рідкі фази. Відповідно до правила фаз варіантність системи буде визначатись рівнянням: С = к + 1 — р. У точці d система однофазна (рідкий розчин), отже, С — 3 — 1 = 2, тобто можна одночасно змінювати температуру і концентрацію, не змінюючи числа фаз. У граничній точці е починається розшарування суміші, а тому р = 2. Варіантність С при цьому зменшується до одиниці, тобто склад співіснуючих шарів рідин залежить від температури. Суміш у точці f буде розпадатися па два шари — g і h. У критичній точці розчинення с система нонваріантна, тобто склад співіснуючих шарів рідші 84 однаковий і число компонентів зменшується па одиницю. Іншим прикладом систем, у яких перебувають в рівновазі дві фази змінного складу, може бути бінарна суміш летких рідин у контакті з їх насиченою парою. Діаграма стану подібних систем при постійному тиску наведена на рис. 2.12. Лінія Т A dbТ B — лінія пари, за допомогою якої встановлюють залежність складу пари від складу рівноважної з ним рідини. Залежність температури початку кипіння рідини від її складу встановлює лінія ліквідусу ТAсeТB. Область І па цьому рисунку — пар, а область II — рідкі суміші. У цих областях система біваріантна. Область ІІІ відповідає гетерогенним сумішам, тобто моноваріантним системам. Так, точка а відповідає рівновазі двох фаз, склад яких визначається подою de та перпендикулярами dd і ее на вісь абсцис. Точка d на цій осі відповідає складу пари, точка e — складу рідини. Рис. 2.12. Залежність температури кипіння бінарної суміші від складу рідкої та газоподібної фаз. 2.4.5. Тверді розчини та їх класифікація При кристалізації сумішей у вигляді твердої фази можуть виділятися не індивідуальні речовини, а змішані кристали, тобто однорідні суміші, що знаходяться у твердому стані. Такі суміші (їх називають твердими розчинами) дуже поширені в природі. Поняття про тверді розчини було введено в науку Вант-Гоффом наприкінці XIX ст. Як було встановлено рентгеноструктурним аналізом, тверді розчини можуть бути трьох тинів: заміщення, впровадження 85 та вилучення. При утворенні твердих розчинів заміщення у вузлах кристалічної решітки даної речовини атоми (чи молекули) заміщуються атомами іншої речовини. В інших випадках розчин утворюється завдяки входженню одних атомів в пустоти кристалічної решітки іншої речовини. Тверді розчини вилучення характеризуються наявністю в кристалах незаповнених вузлів решітки, тому їх називають дефектними. Подібні кристали утворюються іонами елементів зі змінною валентністю. Розглянемо, наприклад, кристал, що містить Fe3+ і які—небудь аніони. Нехай далі деяка частина Fе3+ відновилася до Fе2+. Тоді в кристалі з'являються зайві аніони, що виходять з решітки, залишаючи в ній незаповнені вузли. Розчини заміщення утворяться тоді, коли атоми першого та другого компонента, що заміщують їх в кристалічній решітці, близькі за розмірами і майже не відрізняються за своїми енергетичними характеристиками. Якщо частки дуже відрізняються за розмірами, то виникають тверді розчини впровадження. Такі системи, наприклад, утворюються при розчиненні газів у твердих металах. Взаємна розчинність речовин у твердому стані може змінюватися в широких межах так само, як і для рідин. При цьому можливі такі три випадки: повна нерозчинність, обмежена розчинність і необмежена розчинність компонентів. При утворенні твердих розчинів впровадження розчинність компонента, що впроваджується, обмежена: у системі можуть утворюватися насичений розчин першого компонента в другому і другого в першому. Таким чином, у системі утворюються перервні ряди твердих розчинів. Якщо утворяться розчини заміщення, компоненти необмежено розчиняються один в одному. Це відбувається тоді, коли атоми обох компонентів розчину майже не відрізняються один від одного як за розмірами, так і за енергетичними характеристиками. При необмеженій розчинності компонентів у системі утворяться безперервні ряди твердих розчинів. Взаємна розчинність твердих речовин, як і рідин, залежить від зовнішніх умов, у першу чергу від температури. Зі зниженням температури взаємна розчинність часто зменшується, і тоді твердий розчин може розділятися на два насичених твердих розчини (першого компонента в другому і другого в першому). Такий процес називається розривом суцільності твердих розчинів. Він подібний до розшарування суміші рідин, 86 що необмежено змішуються при зниженні температури нижче верхньої критичної температури розчинення. Контрольні запитання 1. Охарактеризувати такі поняття, як фаза, компонент, незалежний компонент, ступінь вільності, варіантність системи. 2. Доведення правила фаз Гіббса. 3. Застосування правила фаз Гіббса до однокомпонентних систем. Використання діаграм стану для встановлення зв'язку між основними параметрами однокомпонентних систем. 4. Аналіз діаграми стану води. 5. Доведення рівняння Кланейрона - Клаузіуса та його застосування для аналізу процесів випаровування і плавлення. 6. Основи фізико-хімічного аналізу, принципи безперервності та відповідності. 7. Застосування правила фаз Гіббса до двокомпонентних систем. 8. Рівновага кристали — рідина. Основи термічного аналізу, типи кривих охолодження та методика побудови діаграм плавкості. 9. Побудова та аналіз діаграм плавкості двокомпонентних систем, компоненти яких у твердій фазі не взаємодіють (системи з евтектикою). 10. Побудова та аналіз діаграм плавкості двохкомпонентних систем, компоненти яких утворюють хімічні сполуки. 11. Побудова та аналіз діаграм плавкості двокомпонентних систем, компоненти яких утворюють безперервний ряд твердих розчинів (необмежено змішуються у твердій фазі). 12. Побудова та аналіз діаграм плавкості двокомпонентних систем, компоненти яких утворюють перервний ряд твердих розчинів (обмежено змішуються у твердій фазі). 13. Характеристика різних способів зображення складу систем. Аналіз діаграм плавкості. 87 Розділ 3.ХІМІЧНА КІНЕТИКА І КАТАЛІЗ Хімічна кінетика розглядає закономірності, які визначають залежність швидкості хімічної реакції від будови молекул реагуючих речовин, їх концентрації, температури, властивостей середовища, присутності каталізатора інших факторів, а також вивчає механізми хімічних реакцій. Хімічна кінетика, як і термодинаміка, є теоретичною базою різноманітних технологічних процесів. Вона дає можливість знайти найзагальніші методи з'ясування механізмів реакцій, шляхи вдосконалення нових технологічних процесів, у тому числі у харчовій промисловості, розрахувати апаратуру та обладнання. У хімічній кінетиці використовують як методи квантової механіки, молекулярної статистики і термодинаміки, так і специфічні методи. Прості речовини та хімічні сполуки, які вступають у реакцію, називають вихідними речовинами. Кіпцеві речовини, які утворюються в реакції і не зазнають змін, називають продуктами реакції. Речовини, що виникають па інших стадіях хімічного процесу, називають проміжними, а реакції утворення та витрачення цих речовин — проміжними реакціями. Загальним кінетичним критерієм реакційної здатності хімічної системи є швидкість реакції. Більшість хімічних реакцій — це складні процеси, які проходять через низку послідовних і паралельних стадій. Реакції, які відбуваються в одну стадію, називають елементарними. Кожна елементарна реакція відбувається з певною швидкістю і може впливати на швидкість усього процесу. 3.1. Швидкість хімічної реакції Швидкістю хімічної реакції и називають зміну концентрації будьякої речовини, яка бере участь у реакції, за одиницю часу : ( 3 .1 ) Як правило, швидкість реакції обчислюють за концентраціями вихідних речовин і тому похідна dс/dτ від'ємна, оскільки концентрації цих речовин з часом зменшуються. Тому в правій частині рівняння ( 3 .1 ) стоїть знак мінус. Швидкість реакції завжди додатна. Існує також визначення швидкості реакції через продукти хімічної 88 реакції: (3.2) В основі одпостадійних реакцій лежить закон дії мас (закон Гульдберга і Вааге), згідно з яким швидкість хімічної реакції пропорційна добутку концентрацій реагуючих речовин. Причому кожну з концентрацій беруть у ступені, що дорівнює стехіометричному коефіцієнту, який стоїть перед формулою даної сполуки в реакції (n 1 n2, n3 ,....0) (3.3) Коефіцієнт пропорційності К для даної реакції при сталій температурі є величиною сталою, його називають константою швидкості реакції, оскільки вона не залежить від концентрації реагуючих речовин і часу. Із рівняння (3.3) випливає, що при С] = С2 = С3 = 1 швидкість реакції чисельно дорівнює константі швидкості, яку іноді називають питомою швидкістю реакції. Відносно кінетики хімічні реакції поділяють за ознакою молекулярності та порядку реакції. За кількістю молекул, що беруть участь в елементарному хімічному акті, визначають молекулярність реакції Молекулярність реакції завжди є цілим додатним числом: 1, 2, рідко 3. За цією ознакою розрізняють моно-, бі-, тримолекулярні реакції. Реакції вищої молекулярності па практиці не трапляються. Це пояснюється тим, що вірогідність одночасного зіткнення чотирьох і більше молекул дуже мала. До мономолекулярних реакцій належать реакції ізомерізації, дисоціації та розкладу, наприклад До бімолекулярних належать реакції, в яких елементарний акт відбувається при зіткненні двох однакових або різних молекул: До тримолекулярної належить реакція У більшості випадків за рівнянням реакції неможливо дійти висновку 89 про її молекулярність, оскільки воно не відбиває наявності проміжних стадій. Багатостадійність реакції не дає можливості вивчити кінетику процесу взагалі. З огляду на це кінетичні реакції зручніше характеризувати не молекулярністю, а порядком. Порядок реакції визначається за рівнянням, яке виражає залежність швидкості реакції від концентрації реагуючих речовин і дорівнює сумі показників ступенів концентрацій. У багатостадійних реакціях загальна швидкість процесу визначається стадією з найбільш малою константою швидкості. Таку стадію називають лімітуючою. Сукупність усіх стадій, з яких складається процес перетворення вихідних речовин у продукти реакції, називають механізмом хімічної реакції. Для складних реакцій молекулярність і порядок, як правило, не збігаються. Отже, порядок реакції характеризує формальну кінетичну залежність швидкості реакції від концентрації реагуючих речовин, а молекулярність — елементарний механізм окремої стадії складного процесу. Ці поняття збігаються тільки для простих за механізмом реакцій. З підвищенням температури швидкість хімічної реакції, як правило, зростає. Для приблизної оцінки вилину температури на швидкість реакції для невеликого інтервалу низьких температур можна використовувати правило Вант-Гоффа, згідно з яким підвищення температури па 10°С збільшує швидкість хімічної реакції у 2—4 рази: (3.4) Аналітичну залежність швидкості хімічної реакції від температури експериментально встановив Св.Арреніус: (3.5) де Е — енергія активації реакції. Після інтегрування рівняння (3.5) має вигляд (3.6) 90 або в експоненціальній формі (3.7) де К0 — стала інтегрування, яку називають передекспонеціальним множником. До рівняння Арреніуса входять дві сталі величини К0 та Е, які практично не залежать від температури. Тому визначивши експериментально константи швидкості при кількох температурах, можна розрахувати енергію активації Е, інтегруючи рівняння (3.7): (3.8) Звідки (3.9) Визначивши Е за (3.9), знаходимо К0 . Рівняння (3:7) можна записати у вигляді Це рівняння є пригою в координатах lg K – 1/T куга нахилу цієї прямої (3.10) звідки (3.11) Енергію активації, обчислену за цим рівнянням, називають ефективною енергією активації. Розглянемо фізичний зміст поняття «енергія активації». Згідно з теорією Арреніуса хімічна взаємодія відбувається лише при зіткненні частинок з достатньо високим рівнем кінетичної енергії. Такі молекули 91 (частинки) називають активними, або реакційноздатними. Щоб молекули могли вступити у хімічну взаємодію, вони повинні мати певний надлишок енергії порівняно з її середнім значенням. Цей мінімальний надлишок енергії у перерахунку на один моль речовини називається енергією активації Е. 3.2. Класифікація хімічних реакцій Хімічні реакції умовно поділяють на групи, які розрізняють за будьякою специфічною особливістю. Наприклад, за агрегатним етапом середовища — це реакції в газовій фазі, розчинах і твердому середовищі. За агрегатним станом реагуючих речовин, продуктів реакції і середовища реакції поділяють на гомогенні та гетерогенні. У гомогенних хімічних реакціях вихідні речовини, продукти реакції та середовище утворюють одну фазу. У гетерогенних реакціях реагенти перебувають у різних фазових станах. До таких реакцій належать також хімічні реакції, які відбуваються на межі поділу фаз. За специфікою елементарного акту реакції поділяють на ланцюгові та електрохімічні, а за складністю — на прості та складні. До простих належать реакції, які відбуваються в одну стадію. Реакції, що відбуваються в кілька стадій, називають складними. Реакції поділяють також па односторонні, тобто практично незворотні, та двосторонні, які закінчуються при досягненні стану рівноваги. Часто перші називають кінетично незворотними реакціями, оскільки швидкості прямої та зворотної реакцій різко відрізняються. Другий тип реакцій називають кінетично оборотними, оскільки швидкості прямої та зворотної реакцій с порівняними. Поняття кінетичної оборотності не слід змішувати з поняттям термодинамічної оборотності. 3.3. Кінетика односторонніх простих реакцій Для простої реакції першого порядку кінетичне рівняння мас вигляд (3.12) Поділимо змінні: (3.13) 92 Проінтегруємо ліву частину рівняння від нуля до т, а праву від С0 до С: (3.14) або (3.15) де С0 — початкова концентрація речовини, яка відповідає моменту часу, що дорівнює нулю; С — концентрація речовини, яка відповідає часу τ. (3.16) Часто для кінетичної характеристики реакції використовують період напіврозпаду 1/2 час, за який прореагує половина початкової кількості речовини С — С0/2. Підставивши де значення в (5.15), для реакції першого порядку дістанемо (3.17) Для реакції першого порядку період напіврозпаду не залежить від концентрації вихідної речовини і обернено пропорційний константі швидкості реакції. Деякі бімолекулярні реакції відбуваються за законами реакцій першого порядку. Це можливо годі, коли один із компонентів міститься у такому великому надлишку, що його концентрація практично не змінюється з часом. Класичним прикладом такої реакції може бути реакція гідролізу (інверсії) сахарози у водному розчині. Такі реакції називають псевдомономолекулярними. Реакції гідролізу сахарози відбувається за рівнянням: Якщо воду взяти у великому надлишку, то швидкість інверсії (гідролізу) не буде практично залежати від концентрації води. Тому кінетичне рівняння цієї реакції матиме вигляд: 93 Для реакції другого порядку тішу 2А gG + rR кінетичне рівняння має вигляд (3.18) коли С G = С R . Після інтегрування маємо (3.19) або (3.20) Для періоду напіврозпаду (3.21) Отже, у реакціях другого порядку період напіврозпаду 1/ 2 залежить3 ід початкової концентрації. 3.4. Способи визначення порядку реакції Для експериментального визначення порядку реакції використовують методи підстановки, визначення періоду напіврозпаду реакції та графічним методами. Метод підстановки. Експериментальні дані зміни концентрації реагуючих речовин з часом підставляють у кінетичні рівняння першого, другого та інших порядків. Порядок реакції визначають за рівнянням, яке найкраще задовольняє умовам сталості константи швидкості. Метод визначення періоду напіврозпаду реакції. Якщо період напіврозпаду не залежить від початкової концентрації вихідної речовини, то йдеться про реакцію першого порядку; якщо він обернено пропорційний початковій концентрації — це реакція другого порядку. Графічний метод. Перепишемо рівняння (3.15) та (3.19) у вигляді 94 (3.22) (3.23) Рис. 3.1. Графічне визначення константи швидкості реакції першого порядку. За експериментальними даними зміни концентрації С з часом будують графіки в координатах lпС — та 1/c — . Кожне кінетичне рівняння є прямою лінією тільки у відповідних координатах. Так, для реакції першого порядку пряму одержуємо в системі координат lпС— для реакції другого порядку — у системі 1/c (рис. 3.1), (рис. 3.2). За тангенсом кута нахилу прямих можна визначити константу швидкості реакції. Відрізок на осі ординат lп С0 та 1/Со дозволяє знайти Со шляхом екстраполяції, якщо початкова концентрація розчину не відома. Рис.3.2. Графічне визначення константи швидкості реакції другого порядку. 3.5. Кінетика складних реакцій До складних реакцій належать послідовні, паралельні, спряжені, оборотні та ін. У складних реакціях хімічний процес 95 протікає не шляхом прямого переходу молекул вихідних речовин у молекули продуктів реакції, а складається з кількох стадій. Кожну, з цих стадій можна розглядати як самостійну хімічну реакцію. Реакції, що йдуть шляхом прямого переходу реагуючих частинок у продукти реакції, називають елементарними. Існує положення про незалежність протікання елементарних реакцій, згідно з яким константа швидкості елементарної реакції не залежить від того, чи відбуваються у даній системі одночасно інші елементарні реакції. Кожна елементарна реакція описується своїм кінетичним рівнянням. Кінетичне рівняння складної реакції, як зазначалося, визначається лімітуючою реакцією. Розглянемо деякі складні реакції. Двосторонні реакції. Наприклад, двостороння реакція першого,порядку відбувається за такою схемою: Загальна швидкість реакції прямої та зворотної реакції дорівнює різниці швидкостей (3.24) Припустимо, що и початковий момент концентрація речовини А дорівнювала а, а речовими В - b, зміна концентрації за час дорівнює X. Тоді рівняння (3.24) має вигляд (3.25) У стані рівноваги швидкість двосторонньої реакції дорівнює нулю. Із (3.25) маємо (3.26) де К — константа рівноваги; Хр — концентрація у стані рівноваги. Константа рівноваги дорівнює співвідношенню констант швидкостей прямої та зворотної реакцій. Послідовні реакції. Послідовними реакціями називають хімічні (або технологічні) процеси з проміжними стадіями. Можна сказати, що практично майже всі хімічні процеси є багатостадійними послідовними реакціями. Механізм таких реакцій часто невідомий. Тому складають вірогідну схему 96 проходження реакції за стадіями і визначають загальне кінетичне рівняння сумарної реакції. Такі розрахунки дуже складні, якщо брати до уваги, що реакція в цілому й окремі її стадії можуть бути зворотними. Тому розглянемо найпростіший випадок — мономолекулярну незворотну послідовну реакцію k1 k2 A B C в якій відбувається дві односторонні мономолекулярні реакції. Речовина В є проміжним продуктом у процесі отримання речовини С. Прикладом такої реакції може бути радіоактивний розпад радію або гідроліз крохмалю у водному середовищі: крохмаль декстрин мальтоза глюкоза. Ця реакція відбувається у присутності каталізатора і при надлишку води. Розглянемо випадок, коли константи швидкості К1 і К2 різняться не більше, ніж на порядок. Тоді обидві стадії є лімітуючими. Якщо К2 >> К1 або К1>> К2 , то швидкість сумарної реакції дорівнює швидкості найповільнішої проміжної реакції. У першому випадку це перша стадія, а в другому — друга. Паралельні реакції. Для таких реакцій вихідна речовина змінюється в двох або більше напрямках. Розглянемо просту паралельну реакцію першого порядку Кінетику цієї реакції можна описати рівнянням дe (3.27) X — зміна концентрації речовини А з часом . Для розрахунку констант швидко сті К 1 і К 2 , записуємо ще одне рівняння: (3.28) де X1 , X2 - концентрація речовини відповідно В та С за час ; Н— стала, яка не залежить під часу. До такого типу реакції належить розклад бертолетової солі при нагріванні: 97 Загальна швидкість паралельної реакції, стадії якої значно відрізняються за швидкістю, визначається швидкістю найскорішої реакції. Спряжені реакції. Такі реакції відбуваються за схемами: (I) (II) У таких реакціях речовина В індукує II реакцію і є її індуктором. Речовину С називають акцептором. Загальна для обох реакцій речовина А дістала назву актора. Прикладом спряженої реакції може бути окислення сульфату заліза та йодоводню пероксидом водню: (I) (II) Йодоводень пероксидом не окислюється, але при окисленні сульфату заліза він окислюється разом з ним. Тому реакція ( І ) проходить самостійно, а реакція (I I ) — тільки у присутності реакції ( І ) . У цих реакціях Н 2 О 2 є актор, FеSО 4 — індукує реакцію ( I I ) . HJ— акцептор. 3.6. Теоретичні уявлення хімічної кінетики Константа швидкості простої реакції у першу чергу визначається закономірностям», які характеризують проходження елементарного акту. У процесі елементарного хімічного акту змінюється положення ядер атомів і електронної густини в частинках, внаслідок чого розриваються окремі зв'язки або виникають нові хімічні зв'язки. Особливості кожного елементарного акту визначаються кількістю молекул, що беруть участь у ньому. їх будовою та характером реакційних центрів. Елементарний акт супроводжується взаємним переходом енергії поступального руху молекул у внутрішню енергію руху ядер та електронів, а також в обертальну енергію системи. При цьому утворюються нові частинки: молекули, радикали, іони. Стан реагуючої системи, коли змінюється положення ядер, що приводить до розривання 98 окремих зв'язків і виникнення нових, називають перехідним. Кожний елементарний акт проходить через перехідний стан.' 3.6.1. Теорія активного комплексу або перехідного стану Теорію активного комплексу розробив Ейрінг (1935), водночас із ним її запропонували Евапс і Поляні. Розглянемо механізм реакції: При наближенні атома А до молекули ВС послаблюється зв'язок В—С і виникає зв'язок А—В. До утворення молекули АВ і атома С система проходить через активний комплекс АВС*, коли атом В однаковою мірою належить вихідний молекулі ВС та молекулі АВ продукту реакції: Рис. 3.3. Зміна потенціальної енергії системи при хімічній реакції Активний комплекс не є молекулою або проміжною сполукою, оскільки реагуючі молекули в перехідному етапі мають максимальну енергію і система нерівноважна. Під час реакції змінюються відстані між А— В і В—С, що призводить до зміни потенціальної енергії системи. Розглянемо зміну потенціальної енергії Р системи під час даної реакції (рис. 3.3), де Р1 — потенціальна енергія систем и до р еа к ці ї (А + ВС ), а Р2 — потенціальна енергія системи (АВ + С), яка утворилася внаслідок реакції. 99 Для переходу від Р1 до Р2, система має подолати енергетичний бар'єр, величина якого залежить від будови електронних оболонок частинок, що взаємодіють. Для такого переходу існує найвигідніший енергетичний шлях Р1РР2. Точка Р і сусідні з нею ділянки є областю існування активного комплексу АВС (область нестійкості системи). Отже, активний комплекс немов би скочується з перевалу Р у долину Р2. розпадаючись на продукти реакції (АВ + С). Різниця між потенціальними енергіями вихідних речовин і активного комплексу в точці Р дорівнює енергії активації Е1 прямої реакції. Отже, якщо молекули вихідних речовин матимуть енергію Е1 вони зможуть подолати потенціальний бар'єр і перейти у кінцеві продукти реакції. Відповідно Е2 є енергією активації зворотної реакції. Різниця між цими величинами дорівнює тепловому ефекту реакції: (3.29) 3.6.2. Теорія активних зіткнень Теорію активних зіткнень розробив Арреніус. Вона ґрунтується на тому, що елементарний хімічний акт відбувається в момент зіткнення активних молекул. Активними називають молекули, які мають енергію, що перевищує енергію активації або дорівнює їй. Згідно з цією теорією елементарна хімічна реакція протікає миттєво. Як бачимо, хімічні реакції відбуваються шляхом поступової перебудови молекул та перерозподілу енергії між хімічними зв'язками в молекулах. Згідно з молекулярно-кінетичного теорією кількість співударів молекул за 1с дуже велика, а частка активних молекул дорівнює лише 10-20...10-10. Якщо ця частка менша за цю величину, швидкість реакції дуже мала, а якщо перевищує її — реакція проходить швидко, іноді миттєво. Енергія активації дорівнює різниці між середнього енергією активних і середньою енергією всіх зіткнень молекул. Отже, що вища енергія активації даної реакції, то за значно вищих температур вона відбувається. Щоб розпочався хімічний процес, необхідна активація системи. Джерела активації можуть бути різними. Так, реакції між вільними атомами та радикалами не потребують активації, оскільки атоми і радикали є активними частинками. Реакції між іонами у розчині відбуваються з невеликою енергією активації, необхідною для дегідратації іонів. Деякі реакції проходять під дією світла (фотохімічні реакції), електричних 100 розрядів, ударів електронів, нейтронів, а-частинок та ін. У гомогенних газових реакціях джерелом активації є особливо сприятливі зіткнення, частка яких визначається за законом розподілу Больцмана. Під час реакції кожна молекула газу змінює своє положення та швидкість. При кожному зіткненні двох молекул відбувається перерозподіл кінетичної енергії між ними залежно під умов співударів, але сума цих енергій залишається сталою. Рис. 3.4. Зміна потенціальної енергії системи при хімічній реакції Отже, у кожний момент часу молекули матимуть різні швидкості. Дж. К. Максвел, використовуючи теорію ймовірності, встановив закон розподілу молекул за швидкостями, згідно з яким можна визначити частку молекул, які мають середню швидкість. Розглянемо графік розподілу молекул за швидкостями (рис. 3.4), де Vт— найвірогідніша швидкість, що залежить від температури. Отже з цією швидкістю рухається найбільша кількість молекул. У хімічній реакції серед N молекул при кожній температурі є N* активних молекул. Згідно із законом Максвела-Больцмана кількість активних молекул (або активних співударів) (3.30) де Е — енергія активації. Отже, у кінетичне рівняння хімічної реакції замість концентрації треба підставляти активну концентрацію. Теорія активних співударів пояснила багато проблем хімічної кінетики. Але через схематичність вона призвела до протиріччя з експериментальними даними. Наприклад, теоретично розраховані швидкості в десятки разів перевищували експериментальні значення (особливо для розчинів). Це 101 пояснюється тим, що співудари молекул розглядалися як зіткнення пружних шарів. Не брався до уваги фактор, який враховує ймовірність певної геометричної конфігурації частинок при зіткненні. Незважаючи, на це теорія активних зіткнень відіграла велику роль у хімічній кінетиці, де з'явилися нові напрямки розвитку теорії елементарних реакцій, які ґрунтуються на законах класичної та квантової механіки. 3.7. Ланцюгові реакції До ланцюгових реакцій належать хімічні процеси, в яких активні частинки (вільні радикали, атоми або іони) з ненасиченими валентностями, вступаючи у реакції, спричиняють виникнення нових активних частинок, які можуть знову взаємодіяти з молекулами. Повторення таких циклів дає реакційний ланцюг. Теорія ланцюгових реакцій складна. Започаткували її академік М.М. Семенов та англійський вчений Хіншелвуд. Будь-яка ланцюгова реакція мас три стадії: зародження, розвиток та обрив ланцюга. Зародження ланцюга починається з утворення активного центра (частинки з вільними валентностями). Такі частинки можуть утворитися при термічному розкладі окремих молекул па атоми або радикали, при освітленні системи або внаслідок дії елементарних частинок з великою енергією. Реакційна здатність активних частинок неоднакова. Вона тим більша, чим більше енергії витрачено на утворення частинки. Добре вивчено ланцюгову реакцію водню з хлором. У темряві ця реакція не відбувається, але при освітленні суміші водню і хлору (хоча б на короткий час) реакція протікає з вибухом. Зародження ланцюга настає при поглинанні молекулою С12 кванта енергії hv. Далі відбувається ланцюгова реакція Ланцюг може припинити зростати внаслідок рекомбінації вільних радикалів у молекулу: 2Сl Сl2 і далі відбувається обрив ланцюга. 102 Такі реакції називають реакціями з нерозгалуженим ланцюгом. Під час кожного елементарного акту взаємодії вільного радикала з молекулою утворюється лише один новий вільний радикал. Якщо в елементарному хімічному акті виникає два або більше нових вільних радикалів, має мо реакцію з розгалуженим ланцюгом. Розглянемо взаємодію водню з киснем: За нормальних умов реакція утворення води практично не відбувається через високу енергію активації. За наявності активних частинок ОН*, Н*, О* реакція горіння водню розвивається за механізмом ланцюгових реакцій з розгалуженим ланцюгом: Або А далі реакція з розгалуженим ланцюгом Сумарну реакцію в ланці ланцюга можна записати так: Ланцюг може обірватися так само, як і в реакціях з нерозгалуженим ланцюгом, внаслідок рекомбінації вільних радикалів у молекулу. Якщо ланцюг не обривається, реакція розвивається лавиноподібно і призводить до вибуху. До ланцюгових реакцій належать реакції полімеризації. Для одержання полімерних матеріалів часто в систему вводять речовини (так звані ініціатори), які легко розпадаються на вільні радикали. Це переоксиди бензоїлу (С6Н5СОО)2, ацетилену (СН3СОО)2, водню Н2О2 та ін. Розглянемо механізм полімеризації хлоропрену у присутності оксиду бензоїлу: 103 і т.д. Отже, персоксид бензоїлу розпадається на радикали, які за місцем подвійного зв'язку приєднуються до мономера, утворюючи нову частинку з вільною валентністю. Реакція триває доти, доки ланцюг не обірветься з тих чи інших причин. 3.8. Кінетика гетерогенних процесів Гетерогенними називають процеси, які відбуваються на межі поділу фаз. До них належать процеси розчинення, кристалізації, випаровування, конденсації, хімічні та електрохімічні реакції на межі поділу фаз та ін. На швидкість гетерогенних процесів впливає багато факторів, які часто неможливо врахувати. Тому теоретично обґрунтувати той чи інший процес дуже важко. Розглянемо деякі основні положення механізму гетерогенного процесу: Ця реакція відбувається на межі поділу фаз Zп(т) — розчин. Гетерогенна реакція складна і складається з таких основних стадій: доставка речовини з розчину до твердої поверхні; хімічна реакція на поверхні твердого тіла; відведення продуктів реакції від твердої поверхні в об'єм розчину. Кожна із цих стадій протікає з певною швидкістю і лімітуючою буде стадія з найменшою швидкістю. Перша стадія — доставка речовини до поверхні поділу фаз 104 відбувається за рахунок конвекції та дифузії. Конвекція — це переміщення всього середовища. Конвекція розчину па межі поділу з твердою поверхнею зумовлена різною густиною розчину в об'ємі і біля поверхні. Дифузія відбувається за рахунок переміщення молекул та іонів речовини у нерухомому середовищі за наявності градієнта концентрації. Згідно із законом Фіка швидкість дифузії dт/dτ пропорційна площі поверхні S та градієнту концентрації dс/dх: (3.31) де ,,,,,,,,,,,,,,,,,,,,,,,Д — коефіцієнт дифузії, який дорівнює кількості речовини, що продифундує за одиницю часу через одиницю площі при градієнті концентрації, який дорівнює одиниці. Одиниця Д — м2/с. Залежність коефіцієнта дифузії від температури та в'язкості розчинника для кулеподібних частинок радіуса r описується рівнянням Стокса — Ейнштейна: (3.32) Швидкість гетерогенних процесів збільшується при перемішуванні, але вплив дифузії в цьому разі не зникає. Незважаючи на те, що перемішування призводить до вирівнювання концентрації більшої час тини об'єму, біля самої поверхні поділу завжди залишається невеликий дифузійний шар, який не перемішується, і концентрація вирівнюється в ньому за рахунок дифузії. Швидкість гетерогенної реакції залежить також від природи та стану поверхні поділу фаз. При збільшенні площі поверхні контакту фаз та її безперервному оновленні під час процесу збільшується також швидкість реакції. 3.9. Каталіз Крім розглянутих факторі», на швидкість хімічної реакції впливають каталізатори. Каталізаторами можуть бути атоми, іони, молекули, які взаємодіють з реагуючими речовинами, впливають на швидкість хімічної реакції і після кожного реакційного циклу виділяються у хімічно незмінному 105 стані. Явище каталізу було відкрито Г.Р. Кірхгоффом 1814 року, а термін «каталіз» був запропонований Й.Я. Берцеліусом 1838 року. Як правило, каталізатори, що прискорюють швидкість реакції, називають позитивними, а каталізатори, що зменшують швидкість реакції — негативними. Наприклад, гідрохінон і а-нафтол гальмують самочинні процеси окислення жирів. Каталіз є дуже поширеним явищем. Відомо багато каталізаторів, але універсальнішим серед них є вода. Дуже велика кількість реакцій відбувається тільки у присутності води. Наприклад, реакції водню з киснем, водню з хлором та аміаку з хлористим воднем. Усі каталітичні процеси можна поділити па три основні групи — гомогенні, гетерогенні та ферментативні. Каталізатор може вступати у взаємодію з однією або всіма реагуючими речовинами, при цьому утворюється проміжна сполука АХ. Після кожного елементарного хімічного акту каталізатор відновлюється і може вступати у взаємодію з новими молекулами реагентів. Природа сил, на яких ґрунтується взаємодія каталізатора з реагентами, така сама, як і для хімічних сполук — це ковалентний зв'язок, донорно-акцепторна і кулонівська взаємодія, водневий зв'язок та ін. Для утворення хімічного зв'язку необхідна повна відповідність молекулярних орбіталей реагуючих молекул і каталізатора за енергією та симетрією (специфічна дія каталізатора). Каталізатори, незалежно від їх природи, прискорюють (або сповільнюють) тільки термодинамічно можливі реакції. Як відомо, каталізатор входить до складу проміжної сполуки, а термодинамічна можливість процесу визначається різницею вільної енергії початкового та кінцевого станів системи. Хімічний процес у присутності каталізатора відбувається у напрямі зменшення вільної енергії і прискорюється за рахунок зниження енергії активації, що призводить до збільшення концентрації активованих комплексів. Наприклад, швидкість реакції без каталізатора (3.33) а з каталізатором (3.34) де Сх. — концентрація активованого комплексу. Тоді їх підношення 106 (3.35) де т — відношення швидкостей, або відношення концентрацій активованого комплексу С*х у каталітичній й некаталітичній С*0 реакціях. Якщо температура кімнатна і Е 0*- Е x* = 50 кДж/моль, то К 0 /Кх =1010 Тобто, щоб прискорити реакцію за допомогою каталізатора в 1000 разів, необхідна така концентрація активованого комплексу: З цього прикладу видно, що швидкість каталітичної реакції пропорційна концентрації каталізатора. Каталізатори змінюють швидкість реакції, але не порушують рівноваги у рівноважних (оборотних) хімічних реакціях, оскільки вони однаковою мірою прискорюють (зменшують) швидкості прямої та зворотної реакцій. Оскільки каталізатори входять до складу активованого комплексу, воші змінюють термодинамічні параметри Н*, S*, G* і тим самим впливають на швидкість та константу швидкості реакції. Каталітичні реакції за своєю природою належать до складних реакцій і частіше до послідовних. Тому лімітуючою буде стадія, що проходить з найменшою швидкістю. На практиці часто застосовують не окремий каталізатор, а їх суміші. Такі складні каталізатори називають змішаними. Наприклад, використовуючи СиО і МпO2 із домішками деяких металів, проводять реакцію окислення оксиду вуглецю при кімнатній температурі. Швидкість каталітичної реакції можна істотно прискорити за рахунок введення в систему речовин (активаторів), які підвищують активність каталізатора. З часом активність каталізаторів зменшується внаслідок блокування його активних центрів отрутами. Це сполуки сірки, фосфору, миш'яку, ртуті, оксиди вуглецю, ціанисті сполуки та їжі. Каталітичні отрути можуть також утворювати стійкі поверхневі хімічні сполуки і тим самим зменшувати активність каталізатора. 107 3.10. Гомогенний каталіз Процеси, в яких реагуючі речовини і каталізатор перебувають в одній фазі й утворюють гомогенну хімічну систему належать до гомогенного каталізу. Більшість реакцій, що відбувається у розчинах, є гомогенними каталітичними реакціями. Це реакція інверсії сахарози, що відбувається у присутності кислоти, реакції етерифікації, омилення ефірів та ін. Розглянемо кислотно-лужний каталіз. За Дж. Бренстедом кислота віддає протопи (донор протонів), а луг — їх приєднує (акцептор). Наприклад, кислота відщеплює протон а луг — приєднує його У розчинах протон у вільному стані не може довго існувати. Тому у процесі відщеплення-приєднання протона беруть участь дві пари спряжених кислоти та лугу — відбувається протолітична реакція: При кислотному каталізі па першій стадії реакції протон від каталізатора (кислоти) АН передається до реагуючої речовини S на другій стадії протонізована форма речовини SH+ розпадається на продукти реакції Р і Д і відбувається регенерація каталізатора. Розглянемо механізм гомогенного каталізу на прикладі реакції гідролізу складного ефіру у присутності каталізатора — сильної кислоти: Реакція відбувається з великою швидкістю, практично миттєво, встановлюється квазірівноважний стан. Карбонільна група протонується, 108 електронна густина відтягується від атома вуглецю і атом кисню отримує позитивний заряд. Присутність позитивного заряду на атомі кисню різко змінює властивості сусіднього атома вуглецю, за рахунок чого його реакційна здатність підвищується приблизно в 1000 разів і він активно вступає у взаємодію з молекулою води. Реакція відбувається за рахунок зниження енергетичного бар'єра: Ця стадія буде лімітуючою і визначатиме швидкість реакції. 3.11. Ферментативний каталіз Ферменти або біокаталізатори, які входять до складу клітин, каталізують хімічні реакції в організмі. Висока активність та специфічність дії ферментів дає у достатній кількості необхідні для життєдіяльності сполуки або знищує непотрібні речовини, які накопичуються у процесі життєдіяльності живого організму. Ферменти мають високу каталітичну активність. Наприклад, для життєдіяльності людини, яка займається творчого працею, необхідно кожний день споживати стільки їжі, щоб при повному згорянні вона виділяла 8380 кДж теплоти. Для цього достатньо з'їсти 0,5 кг цукру, який в організмі повністю окислиться за одну добу. Якщо цей цукор розчинити в 30...40 л води (стільки води в тілі людини) і провести реакцію окислення киснем при температурі тіла людини (37 ° С ) , то на цей процес витратиться 100000 років. Отже, процес окислення цукру в організмі протікає у 100000 разів швидше, ніж при такій самій температурі у розчині. Ферменти мають високу специфічність та селективність Е. Фішер образно порівняв дію фермента і субстрата (реагуючої речовини) з ключем та замком. Як ключ відкриває тільки певний замок, так і фермент каталізує тільки певну реакцію. Наприклад, гідролази каталізують реакції гідролізу, а ізомерази — реакції ізомерізації. Ферменти — це високомолекулярні білкові сполуки, які складаються з амінокислот, взаємозв'язаних нептидним зв'язком —СО — NH— у 109 ланцюжки будь-якої довжини. Ди-, три-, поліпептиди можна одержати з молекулярною масою 4 10 ...10 6. Макромолекула білку має фібрілярну (лінійну) або глобулярну (еліпсоподібну) структуру. Каталітичну активність проявляють тільки глобулярні білки. Ферментативна каталітична реакція — це складний багатоступеневий процес, який відбувається на активних центрах ферменту. Активний центр складається із каталітичного і просторового центрів. Перший відповідає за хімічну природу каталітичної реакції (специфічна дія каталізатора), другий — за спорідненість до субстрату. Необхідною умовою каталітичної дії фермента мас бути структурна відповідність активного центру ферменту та субстрату. При цьому відбувається перебудова конформації пептидного зв'язку ферментного білка таким чином, що утворюються допоміжні зв'язки між субстратом та реакційноздатними функціональними групами білка, які каталізують розщеплення субстрата. Ферментативні реакції підпорядковуються загальним правилам каталітичних реакцій. Ферменти не збільшують виходу продуктів реакції, вони вибирають найбільш швидкий шлях реакції, при цьому утворюються такі самі продукти, що й без каталізатора. Фермент після реакції залишається незмінним і вступає повторно в реакцію з другого молекулою субстрату. Фермент може перетворюватись тисячі разів за секунду. На активність ферментів впливають активатори, інгібітори, каталітичні отрути, властивості середовища. Ферменти високоспецифічні активні при кімнатній температурі та атмосферному тиску. Активатори прискорюють каталітичні реакції і діють у напрямку, протилежному дії інгібітора. Наприклад, активація протеїнази папаїна синильною кислотою ґрунтується на зв'язуванні кислотою іонів важких металів, які інгібують активність цього фермента. В інших випадках активатор гальмує процес зміни конформації фермента-білка під дією фізичних факторів (рН, температури та ін.). Інгібітори можуть діяти обернено та необернено. Прикладом необерненого інгібування ферментів сульфгідрідними грумами в активному центрі може бути дія йодонтовою кислотою. Обернене інгібування характеризується рівновагою між ферментом та інгібітором. Ця рівновага 110 описується константою рівноваги, яка є мірою спорідненості ферменту до інгібітора. Прикладом оберненого інгібування є реакції, в яких ферментативний каталіз інгібується продуктами реакції. Так, гідроліз крохмалю - або -амілазою обернено інгібується продуктами розщеплення — мальтозою. Між субстратом та інігібітором існує певне кількісне співвідношення. Якщо концентрація інгібітора більша концентрації субстрата [J] > [S],інгібітор взаємодіє з ферментом і вимикає його з реакції, а субстрат не розщеплюється. У випадку, коли вміст субстрата вищий, ніж інгібітора [S] > [J], З ферментом буде зв'язуватися субстрат, який розкладається на продукти реакції, а фермент відновлюється. Основною характеристикою ферментів, яка відрізняє їх від інших каталізаторів, с висока специфічність — здатність фермента із багатьох можливих реакцій з даним субстратом прискорювати лише певну реакцію. Така вибірковість є характерною відмінністю ферментів від чисто хімічних каталізаторів (платини, нікелю, заліза та ін.). Наприклад, фермент уреаза розкладає сечовину, тобто розриває зв'язок у сечовині, але не може розірвати такий же зв’язок у білків. Як зазначено вище, така висока специфічність ферментів дала можливість Фішеру порівняти фермент з ключем, а субстрат, па який діє фермент, із замком. Механізм ферментативних реакцій на сьогодні вивчений недостатньо, в декілька теорій, що в тій чи іншій мірі описують цей механізм. Наведемо теорію Міхаеліса- Ментена, що пояснює залежність початкової швидкості реакції від концентрації субстрату. Розглянемо схему ферментативної реакції: де F і S — відповідно фермент та субстрат; FS — фермент-субстратний комплекс; P — продукт реакції. Дослід проводиться за таких умов: початкові концентрації ферменту та субстрату відповідно. Початкова швидкість V0 утворення продукту описується рівнянням першого порядку: (3.36) 111 Після складних математичних перетворень отримаємо вираз: (3.37) Якщо виконується умова [F] 0 = [FS], Отримаємо: (3.38) де Рівняння (3.37) с рівнянням Міхаеліса-Ментена для визначення початкової стаціонарної швидкості ферментативної реакції. Добуток К2[F] 0 мас розмірність швидкості реакції, її частіше називають швидкістю ферментативної реакції і позначають m — це швидкість, з якою проходить реакція за умови перебування ферменту у складі комплексу FS. З рівняння (3.37) випливає, що стаціонарна швидкість розглянутої ферментативної реакції за умови [S]0 » [F] о має гіперболічну залежність від концентрації субстрату та лінійну від початкової концентрації ферменту (рис. 3.5, а і б). Ці залежності дійсно характеризують кінетику більшості ферментативних реакцій. Риє. 3.5. Залежність початкової швидкості ферментативної реакції V0 від концентрації субстрату (а) та ферменту (б). За допомогою рис. 3.5 можна визначити константу Міхаеліса Кт. За умови V0 Vm рівняння (3.38) має вигляд: 2 112 (3.39) Тоді Кт=[S]. Ця константа чисельно дорівнює концентрації субстрату, за якої швидкість ферментативної реакції досягає половини свого максимального значення (рис. 3.5, а). її значення залежить від pH, температури, природи субстрату та ін. Найчастіше величина Кm знаходиться у межах 10 -1...10 -6. Значення Vm використовують для характеристики активності ферменту. Одиниця активності — це активність ферменту, що перетворює 1 мкмоль субстрату за 1 с. Більшість ферментів проявляють каталітичну активність за температури 10...60 °С. За вищих температур починає руйнуватися білкова основа ферменту, за нижчих — ферментативна реакція гальмується у зв'язку зі збільшенням в'язкості рідин, що заповнюють клітини. Для більшості ферментів швидкість ферментативної реакції максимальна за рH = 4 10. Нижче наведені оптимальні значення рН для деяких рослинних ферментів: амілаза солоду — 4,9 5,2; амілаза картоплі — 6,7; мальтаза дріжджів — 6,1 6,8; пентаза плодів — 4,3; уреаза сої — 7,5; карбоксилаза — 4,8. Ферменти містяться у всіх живих клітинах, проте розподілені вони нерівномірно. Наприклад, пепсин знаходиться тільки у слизовій оболонці шлунку; трипсин — у підшлунковій залозі; амілаза міститься у великій кількості у підшлунковій залозі, але у невеликій кількості і у крові, м’язах; печінка багата на естеразу, каталазу та аргіназу; уреаза знаходиться у високій концентрації в бобах конвалії (Canavalia ensiformis) та сої. 3.12. Гетерогенний каталіз Гетерогенний каталіз — це каталітичні процеси, які відбуваються па поверхні поділу фаз. При цьому каталізатором є тверда фаза, а реагуючими речовинами найчастіше рідка або газоподібна фаза. Гетерогенно-каталітичні реакції ширше застосовуються у промисловості, ніж гомогенні та ферментативні. Це зумовлено тим, що тверді каталізатори легше відокремити від рідкої або газоподібної фази, в якій містяться реагенти. Каталізатор діє не всією своєю масою, а лише 113 поверхневими активними центрами. Тому швидкість такої каталітичної реакції вже не буде пропорційною масі каталізатора, як у гомогенному каталізі, а залежатиме від питомої площі поверхні каталізатора. У промисловості застосовують каталізатори у вигляді циліндрів, гранул діаметром кілька міліметрів, а також каталізатори, які одержують нанесенням активного агента (платини, паладію) на пористий посій — активоване вугілля, кизельгур, силікагель, алюмогель. Кількість каталітично активного металу у нанесеному каталізаторі не перевищує декілька відсотків, що дає можливість економити дорогоцінні дефіцитні метали. За дуже малих концентрацій нанесеного металу на поверхні носіїв знаходяться не мік рокристали, а невеликі групи атомів, які Кобозсв назвав ансамблями. Він звернув увагу на те, що за збільшенням кількості нанесеного металу на носії активність нанесеного каталізатора проходить через максимум. Наявність максимума вказує на їх;, що носіями каталітичної активності с ансаблі певного розміру, які мають визначену кількість атомів. Теорія Кобозсва дас можливість визначити цю кількість атомів. Для підвищення активності, термодинамічної стійкості, механічної твердості застосовують каталізатори у вигляді багатокомпонентних систем — змішані та промотировані. Змішані каталізатори — це суміш двох або кількох оксидів Al2О3, Сr2О3, СаО і МgO, активність яких є функцією складу. Часто до каталізатора додають активатори (промотори), які не мають каталітичних властивостей, але підвищують каталітичну активність каталізатора. Наприклад, для залізного каталізатора синтезу аміаку таким промотором с оксид алюмінію. Він покриває тонкого плівкою поверхню каталізатора і захищає його від рекристалізації, зберігаючи дефекти у поверхневому шарі, тобто питому активність каталізатора. Під час гетерогенного каталізу, як і гомогенного, активність каталізатора з часом зменшується через його отруєння. Отруєння може бути зворотним або незворотним. Сполуки, що містять сірку, арсен отруюють незворотно багато металічних каталізаторів. Слід зазначити, що невелика кількість отрути суттєво виливає на активність каталізатора. Каталізатори проявляють специфічні (вибіркові) властивості, тобто для одних і тих самих вихідних речовин каталізатори можуть викликати неоднакові процеси з утворенням різних кінцевих продуктів Наприклад, у 114 присутності оксиду алюмінію етиловий спирт при температурі 350°С розкладається на етилен та воду: а при температурі 250°С — на ефір та воду: Якщо замість оксиду алюмінію як каталізатор застосувати мідь, то відбувається дегідрогенізація етилового спирту (при 200 °С) з утворенням альдегіду: У присутності металевого натрію з етилового спирту добувають бутиловий спирт: Специфічність дії каталізатора мас велике значення у промисловості, оскільки дає можливість провести хімічний процес у необхідному напрямі з найбільшою швидкістю, якщо в даній системі термодинамічно можливі кілька неналежних хімічних перетворень. Механізм гетерогенного каталізу складніший, ніж гомогенного. Існує кілька теорій гетерогенного каталізу, проте кожна з них повністю не пояснює механізму цього процесу. Розглянемо деякі з них. Принципово відмінність гетерогенної каталітичної реакції під гомогенної полягає утому, що хімічні процеси відбуваються не в об'ємі реагуючої системи, а на поверхні поділу фаз. Тому при визначенні швидкості такої реакції похідну dс/d необхідно віднести до одиниці площі поверхні S, а замість співвідношення (5.1) записати Для гетерогенно-каталітичних реакцій величину 1dc називають Sd питомою каталітичною активністю (у даному випадку розраховують поверхневу концентрацію). Гетерогенно-каталітичні реакції відбуваються послідовно у декілька стадій. Наприклад, першою стадією є транспортування реагуючих речовин до поверхні каталізатора. Друга стадія — адсорбція молекул субстрату на 115 поверхні каталізатора, третя — реакція на поверхні каталізатора. Четверта стадія відповідає процесу десорбції продуктів реакції з поверхні каталізатора і, нарешті, п'ята — це транспортування продуктів реакції в об'єм системи. Залежно від умов проведення каталітичного процесу та його особливостей, перелічені стадії можуть відбуватися з різною швидкістю. Активність каталізатора характеризується швидкістю реакції на поверхні поділу фаз. Перша і п'ята стадії визначаються законами дифузії. Другою стадією є адсорбція молекул субстрату з газової або рідинної фази на поверхні каталізатора. Адсорбція — самодовільний процес концентрування речовини па поверхні поділу фаз. Розрізняють фізичну та хімічну адсорбцію (хемосорбцію). Фізична адсорбція зумовлена силами міжмолекулярної взаємодії між молекулами субстрату і активними центрами каталізатора. Під час хемосорбції відбувається хімічна взаємодія молекул субстрату з поверхнею твердої фази з утворенням зв'язків ковалентного або полярного характеру. Оскільки адсорбція — це самодовільний процес, вона відбувається зі зменшенням енергії Гіббса і ентропії системи за рахунок упорядковування молекул субстрату в адсорбційному шарі. Тому процес адсорбції є екзотермічним: При хемосорбції також зменшується вільна енергія за рахунок взаємодії каталізатора і субстрату. Залежність хемосорбції від концентрації або тиску описується рівнянням Ленгмюра (3.40) де Г — максимальна кількість субстрату, що може адсорбуватися на каталізаторі; в — величина стала. Або за емпіричним рівнянням Фрейндліха (3.41) де , — емпіричні сталі. Специфічність гетерогенно-кагалітичного процесу, мабуть, зумовлюється хемосорбцією, оскільки хемосорбція як хімічний процес мас 116 вибірковий характер і тому може значною мірою впливати па швидкість та напрям гетерогенно-каталітичного процесу. Великого поширення набули уявлення, що поверхня каталізатора неоднорідна і на ній присутні активні центри. Ці припущення були зроблені Д.П. Коноваловим ще у 1885 р. Пізніше їх розвинув X. Тейлор (1926). Найбільшого поширення дістала мультиплетна теорія каталізу О.О. Баландіна (1930). Мультиплети — це окремі ділянки поверхні каталізатора, які складаються з кількох атомів і на яких відбувається адсорбція молекули субстрату. Мультиплетна теорія ґрунтується на двох принципах: геометричної та енергетичної відповідності. Між мультиплетами та адсорбованими молекулами має існувати геометрична (структурна) відповідність, тобто геометричне розташування силових центрів на поверхні каталізатора (мультиплета) має відповідати розташуванню атомів у молекулі субстрату. Академік О.О. Баландін довів, що для прискорення реакції гідрування та дегідрування шестичленних циклічних вуглеводів С6 Н 6 , С6Н12 використовують каталізатори — метали з гексагональними кристалічними решітками — з міжатомною відстанню (2,5...2,8) • 10-10 м. Але для активації каталітичного процесу необхідна не тільки геометрична відповідність між мультиплетами і субстратом, а й взаємодія між ними. Ця теорія не розглядає молекулярного механізму взаємодії субстрату з каталізатором. М.І. Кобозев (1939) запропонував теорію активних ансамблів, згідно з якою активний центр (ансамбль) каталізатора має складатися з одного-двох атомів металу (рідше шести), що відповідає максимальній активності каталізатора. Подальший розвиток теорії гетерогенного каталізу показав, що механізм гетерогенно-каталітичного акту треба розглядати на основі квантової теорії хімічного зв'язку (тобто теорії молекулярних орбіталей). При цьому необхідно враховувати властивості молекул, які містяться на поверхні твердої фази. Контрольні запитання 1. Дати визначення швидкості хімічної реакції, обґрунтуйте вплив різних факторів на величину швидкості. 2. Що таке константа швидкості хімічної реакції та її фізичний зміст? Від чого залежить константа швидкості хімічної реакції? 117 3. Наведіть рівняння для обчислення константи швидкості реакції першого, другого порядків. 4. Які реакції називаються псевдомолекулярпими? Наведіть приклади. 5. Яким кінетичним рівнянням описується швидкість реакції А + В АВ С за умови, що друга стадія проходить значно швидше, ніж перша? 6. Як практично можна визначити величину швидкості хімічної реакції? Сформулюйте основний закон, який лежить в основі кінетики хімічних реакцій. 7. Що називається молекулярністю і порядком хімічних реакцій? Причіпні, через які не збігаються молекулярні, і порядок реакцій. 8. Як залежить константа швидкості реакції від температури? 9. Особливості кінетики гетерогенних реакцій. 10. Що являють собою фотохімічні реакції? Яким законам вони підпорядковані? 11. Що такс ланцюгові реакції? їх особливості. 12. Що таке енергія активації та її взаємозв'язок із швидкостю реакції? На основі яких даних обчислюється енергія активації хімічних реакцій? 13. Кінетика складних реакцій. 14. Назвіть способи визначення порядку реакцій. 15. Основні положення теорії активних зіткнень? Як вона пояснює перебіг мономолекулярних реакцій? 16. Що таке каталізатори, які їх загальні властивості? У чому полягає специфічність дії каталізаторів? 17. Як пояснити механізм гомогенного каталізу? Роль проміжних сполук. Що таке автокаталіз? 18. Особливості гетерогенних каталітичних реакцій. Роль в них адсорбції та промоторів. 19. Які ви знаєте теорії гетерогенного каталізу? 20. Охарактеризувати особливості ферментативного каталізу. 21. Основні положення теорії активованого комплексу. Чи є принципова різниця між термінами «активований комплекс» 118 та «перехідний стан»? 22. В якому випадку реакція буде кінетично зворотною? Чи можуть такі реакції бути термодинамічно-зворотними? 23. Основи мультиплетної теорії каталізу О.О. Баландіна та теорії активних ансамблів Л.1. Кобозева. їх застосування для вибору каталізаторів. 119 ТЛУМАЧНИЙ СЛОВНИК АБСОРБЦІЯ — поглинання газоподібних речовин об'ємом капілярнопористого твердого тіла, яке супроводжує поверхневу адсорбцію (див. нижче) речовинина межі розподілу фаз газ/тверда речовина. АДСОРБАТ (адсорбтив) — речовина, яка концентрується у поверхневому шарі на межі розподілуфаз (газ/рідина, рідина/рідина, газ/тверде тіло, рідина/тверде тіло). АДСОРБЕНТ — тверда речовина, па поверхні якої відбувається процес адсорбції. Адсорбенти мають розвинену питому поверхню за рахунок подрібнення,пористості. Як адсорбенти використовують капілярно -нористі тіла різної природи, наприклад, силікагелі, глини, глинисті мінерали, кремнеземи,Ґрунти тощо. АДСОРБЦІЯ ПОВЕРХНЕВА — довільний перерозподіл речовини на межі розподілу фаз, пов'язанийзі збільшенням концентрації певної речовини в поверхневому шарі порівняно з об'ємом системи АКТИВНІСТЬ — «ефективна» («виправлена») концентрація речовини в сумішах аборозчинах. Використання активності дозволяє характеризувати термодинамічні властивості неідеальних газових сумішей та розчинів і застосовувати для цього відповідні рівняння ідеальних газових сумішей та розчинів. Для розрахунку активності електроліту вводиться величина коефіцієнтаактивності. КОЕФІЦІЄНТ АКТИВНОСТІ — безрозмірна величина, що показу відмінність активності відконцентрації. Коефіцієнт активності характеризує роботу перенесення 1 моля речовини з реального середовища до ідеального при сталих пара метрах (температура, тиск) та незмінній кількості речовини. Коефіцієнтактивн ості визначають експериментально або оцінюють теоретично. ВИХІД ПРОДУКТІВ РЕАКЦІЇ — величина, яка показує співвідношення між кількістю (або 120 масою) речовини, отриманої в результаті перебігу хімічної реакції за умови, що до сягається стан термодинамічної рівноваги реакції, до кількості (або маси) цієї речовини, розрахованої теоретично за рівнянням хімічної реакції. ДІАГРАМА Діаграма енергетична — графічне зобра ження зміни енергетичного стану системи в результаті фізико-хімічних перетворень речовин. Діаграма фазова (діаграма етапу) — графічна залежність с т а н у системи і фазових рівноваг в ній від зовнішніх умов або від складу системи. ДИСОЦІАЦІЯ Дисоціація електро літи чна — розпад речовини в процесі розчинен ня з утворенням гідратованих (соль ватованих) іонів, що є результатом хімічної взаємодії розчинника і розчиненої речовини. ДИФУЗІЯ Дифузією називається процес довільного вирівнювання концентрації речовини при наявності градієнта концентрації. ЗАКОН Закон Гульдберга-Вааге швидкість хімічної реакції пропорційна добутку концентрацій реагуючих речовин. Причому кожну з концентрацій беруть у ступені, що дорівнює стехіометричному коефіцієнту, який стоїть перед формулою даної сполуки в реакції. Зак он Мак све ла -Б ольц м ан а дає м ож лив ість визн а чити кіль кі сть активних молекул (або активних співударів) в системі. Закон Фік а визначає кількість речовини, яку перенесено через певну площу поверхні внаслідок дифузії. ЕЛЕМЕНТАРНИЙ АКТ ВЗАЄМОДІЇ — с у к у п н і с ть змін с та н у м і н і м а ль н о ї к і ль к о с т і е ле м е н та р н и х ч а с точок, що беруть участь у п роцесі взаємодії. Результатом сукупності величезної кількості послідовних елементарних актів є макроскопічні зміни в системі під час реакції. ЕНЕРГІЯ — це міра інтенсивності руху часточок в системі. Види енергії: кінетична (Е к ), потенціальна (Е п ), механічна, електрична, хімічна, тощо. Для кількісної оцінки величини енергії в термодинаміці введено 121 низку функцій. Енергія активації — це мінімальний надлишок енергії порівняно з її середнім значенням у перерахунку на один моль речовини. Е н е р г і я в н у т р і ш н я ( ї ї ) — фу н к ц і я х а р а к т е р и з у є з а г а л ь н и й з а п а с ен е р г і ї с и с те м и і вк лю ча є вс і ви ди е н е р гі ї р у х у і вз а єм о д і ї ск ла д о вих часточок системи (кінетичну енергію молекулярного руху (поступального і обертального); міжмолекулярну енергію притягання та відштовхування; внутрішньо молекулярну, або хімічну енергію; внутріядерну та енергію електронного збудження тощо). Визначити абсолютне значення внутрішньої енергії термодинамічної системи неможливо, але зміну внутрішньої енергії системи, що змінюється в результаті перебігу певного термодинамічного процесу можна оцінити із 1-го закону термодинаміки. ЕНЕРГІЯ ХІМІЧНОГО ЗВ'ЯЗКУ — кількість енергії, яку треба надати для розриву хімічного зв'язку між атомами або відриву від молекули одного атома. ЕНТАЛЬПІЯ — функція оцінює величину ен ергії системи, яка перебуває в умовах сталого тиску і чисельно дорівнює сумі внутрішньої енергії та добутку тиску й об'єму. ЕНТРОПІЯ - функція стану термодинамічної системи характеризує стан хаосу в системі, причому стан з меншим порядком є більш вірогідни м КАТАЛІЗ — явище зміни швидкості реакції в присутності речовин каталізаторів. (Берцеліус). КАТАЛІЗАТОР — речовина, що змінює швидкість хімічної реакції через входження до складу активного комплексу, але не входить до складу продуктів реакції і на останніх етапах реакції виділяється в незмінному вигляді. КАТАЛІТИЧНІ РЕАКЦІЇ — реакції, перебіг яких відбувається за участю каталізатора. КІНЕТИКА СКЛАДНИХ РЕАКЦІЙ Складними називаються реакції, що мають дві або більше простих реакцій. Кінетика складних реакцій підпорядковані правилу незалежності 122 перебігу елементарних реакцій. Якщо в системі одночасно відбуваються декілька реакцій, то кожна з них є незалежною від інших, а їх швидкість визначається кінетичними рівняннями простих реакцій. КОМПОНЕНТ Компонентом називають індивідуальну хімічну речовину, яка є складовою системи, може бути виділена з неї та здатна існувати самостійно. КОНСТАНТА Константа швидкості хімічної реакції чисельно дорівнює швидкості при одиничних сталих концентраціях реагуючих речовин. Розмірність константи швидкості визначається кінетичним рівнянням реакції. Константа хімічної рівноваги — виражає відношення добутку рівноважних концентрацій (активностей) продуктів реакції до вихідних речовин, взятих у відповідних показниках ступеня (Кс та Ка). Для хімічних реакцій з газоподібними речовинами константа хімічної рівноваги виражається як відношення добутків рівноважних парціальних тисків (фугітивностей) продуктів реакції до вихідних речовин, взятих у відповідних показниках ступеня (КР, Kf). Парціальний тиск компонента в суміші (рf )— дорівнює тому тиску, який мав би цей компонент, коли б він один займав об'єм суміші. Потенціал термодинамічний (Т.П.) [Дж-моль] — характеристична функція стану, зменшення якої в довільному процесі, що проходить при сталих значеннях відповідних незалежних параметрів, дорівнює ко рисній роботі, виконаній системою. Потенціал хімічний — частинна похідна характеристичної функції за масою компонента при сталих величинах відповідних незалежних змінних і масах інших компонентів. ПОРЯДОК ХІМІЧНОЇ РЕАКЦІЇ власний порядок («порядок по реагенту — а, b, с) показник ступеня при молярній концентрації реагента в основному кінетичному рівнянні хімічної реакції; порядок реакції (її) — сума показників ступеня при молярних концентраціях реагентів в основному кінетичному рівнянні. Порядок може бути різним, в тому числі і нульовим, дробовим, негативною або позитивною величиною. Залежить від механізму реакції, концентрації, 123 реагуючих речовин, присутності каталізатора і часто — від температури. ПРАВИЛО Правило важеля — фігуративна точка поділяє копноду на два відрізки, відношення яких дорівнює зворотному відношенню мас врівноважених фаз. Правило Вант-Гоффа — підвищення температури на 10 °С збільшує швидкість хімічної реакції в 2 —4 рази. Правило фаз Гіббса встановлює умови фазової рівноваги в рівноважній гетерогенній термодинамічній системі, на яку впливають, наприклад, лише 2 зовнішніх фактори (температура і тиск). Тоді число ступеней вільності (С) дорівнює числу незалежних компонентів (К) — мінус число ф а з ( Ф ) п л ю с д в а С = К - Ф + 2 Правило Ле Шательє — якщо на систему, що перебуває в етапі стійкої або метастабільної рівноваги, впливати зовнішніми чинниками, змінюючи хоча б одну з умов, які визначають стан рівноваги, то в системі виникають процеси, направлені проти дії зовнішнього чинника. ПРОЦЕС Процес термодинамічний — будь-які перетворення в термодинамічній системі, що супроводжується зміною хоча б одного термодинамічного параметра. Процес термодинамічно зворотний — такий, коли найменший зовнішній чинник змінює напрямок процесу на зворотній без будь-яких змін стану самої системи і зовнішнього середовища. Усі проміжні стани систем є рівноважними, а час його перебігу — нескінченно великий. Часто такі процеси називають рівноважними. Процес термодинамічно незворотний — такий, що не може відбуватись у зворотному напрямі без будь-яких змін стану системи і зовнішнього середовища. Практично усі реальні процеси є термодинамічно незворотними РІВНОВАГА Рівноважний стан — стан системи, при якому за сталих зовнішніх умов термодинамічні параметри не змінюються, а також в системі відсутні потоки речовини і енергії. РОБОТА — А (Дж, кал) - форма передачі енергії від одного тіла до іншого, не 124 пов'язана з переходом теплоти та (або) речовини. СИСТЕМА ТЕРМОДИНАМІЧНА (Т.С) - матеріальний об'єкт, виділений із зовнішнього середовища за допомогою фізичної або абстрактної граничної поверхні і здатний обмінюватися з іншими тілами енергією і (або) речовиною. Стан термодинамічної системи характеризується сукупністю термодинамічних параметрів стану. Система відкрита — обмінюється енергією та речовиною з навколишнім середовищем; Система закрита — о бмінюється із середовищем тільки енергією; Система ізольована — не обмінюється з середовищем ні енергією, ні речовиною. Система гомогенна — між частинами системи відсутні поверхні розподілу, властивості її змінюються монотонно; Система гетерогенна — складається з окремих фаз, розмежованих поверхнями розподілу, на яких термодинамічні властивості змінюються стрибкоподібно. СОЛЬВАТАЦІЯ — сукупність енергетичних структурних змін, що відбуваються в розчині при взаємодії часточок розчиненої речовини з молекулами будь якого розчинника. СТАНДАРТНИЙСТАН — стан 1 моля чистої речовини при сталій температурі та нормальному тиску в найбільш стійкому аг регатному стані. Для газі) стандартний стан — це гіпотетичний або реальний стан, при якому газ, ідо знаходиться при Р = 1,013 — 10 5 На, під порядкований законам ідеальних газів; для індивідуальних твердих та рідких речовин за стандартний стан при температурі Т прийнята модифікація, що є стійкою при даній температурі і Р = 1,013 — 10 5 1Іа\ для розчинів за стандартний стан беруть стан відповідних індивіду а л ь н их р е ч о в и н з а т их ж е Г т а Р і в т о м у ж ф а з о в о м у ст а ні , щ о й розчин; стандартний стан розчиненої речо вини відповідає її станові в безмежно розведеному розчині. 125 СТАНДАРТНІУМОВИ — температура Т = 298 К (25°С); тиск Р = 1атм (101,3 к П а ) ; кількість речовини п = 1 моль; для розчинів — молярна концентрація речовини С(Х) = 1 моль/л; для газової суміші парціальн ий тиск кожного к о м по не нт а м а є д о р і в н ю в а т и о д и ни ці р і = 1 а ш м ( 1 0 1 , 3 кііа). ТЕПЛОТА — q [Дж/моль; кал/моль] — форма передачі енергії від більш нагрітого тіла до менш нагрітого, за рахунок хаотичного руху частинок системи. ТЕПЛОЄМНІСТЬ — I [Дж/К] Теплоємність дійсна — миттєва (С) — це відношення нескінченно малої кількості теплоти, отриманої тілом при нагріванні, до відповідного збільшення температури Теплоємність середня (С) — в інтервалі температур Т — Т2 дорівнює відношенню кількості теплоти (д), отриманої 1 (молем або грамом) речовини, до збільшення температури АГ: Теплоємність питома (Стт), kДж/(К-кг) — кількість теплоти, яку необхідно надати речовині масою 1 кг ( г ) , щоб нагріти її на 1 градус. Теплоємність молярна (С) кДжДК-моль) — кількість теплоти, яку необхідно надати 1 молю речовини для збільшення її температури на одиницю ФАЗА — гомогенна частина гетерогенної термодинамічної системи, обмежена поверхнею розподілу, через яку відбувається стрибкоподібна зміна властивостей. ФУГІТИВНІСТЬ — це тиск реального газу, який дає можливість використовувати його для характеристики поведінки реальних газів. КОЕФІЦІЄНТ ФУГІТИВНОСП характеризує відхилення термодинамічних властивостей реальних систем від поведінки ідеального газу. Література 1. Фізична хімія. За ред.. В.В. Манка: Підручник. – Київ: Центр навчальної літератури, 2007. - 192 с. 2. Голиков Г.А. Руководство по физической химии . - М: Высшая школа. 126 3. 4. 5. 1988, 384 с. Киреев В.А.Краткий курс физической химии. – Москва.: Химия, 1978. – 640 с. Кудряшов И.В., Каретников Г.С. Сборник примеров и задач по физической химиии.- М: Высшая школа. 1991, 384 с. Стромберг А.Г, Семченко Д.П. Физическая химия .-М: Высшая школа, 1988, -496 с. Додаток: Зразок тесту Відпо відь ТЕСТ 0001 1. Ізольованою термодинамічною системою називають будьяке тіло або сукупність тіл, 1. що знаходяться у взаємодії і фактично або уявно виділені з навколишнього середовища. 2. які з навколишнім середовищем не обмінюються масою; 3. які обмінюються з навколишнім середовищем масою та енергією. 4. котрі з навколишнім середовищем не обмінюються енергією та речовиною;. 5. котрі можуть обмінюватися з навколишнім середовищем всіма видами енергії, крім теплової. 2. Закритою термодинамічною системою називають будь-яке тіло або сукупність тіл, 1. що знаходяться у взаємодії і фактично або уявно виділені з навколишнього середовища. 2. які з навколишнім середовищем не обмінюються масою; 3. які обмінюються масою з навколишнім середовищем. 4. котрі з навколишнім середовищем не обмінюються енергією;. 5. котрі можуть обмінюватись з навколишнім середовищем всіма видами енергії, крім теплової. 3. Круговий процес, це процес, 1. в якому система після низки змін повертається до висхідного стану; 2. при якому система може обмінюватись з навколишнім середовищем тільки роботою, але не може обмінюватись теплотою ; 3. який протікає при постійній температурі ; 4. який протікає при постійному об'ємі ; 5. який протікає в умовах постійного тиску . 127 4. Теплота це 1. кількісна міра передавання енергії за допомогою хаотичного руху частинок системи. 2. кількісна міра передавання енергії за допомогою впорядкованого руху частинок системи. 3. енергія поступового руху молекул в системі 4. функція стану термодинамічної системи характеризує стан хаосу в системі 5. повна енергія частинок , що становлять певну речовину 5. Внутрішня енергія це 1. кількісна міра передавання енергії за допомогою хаотичного руху частинок системи. 2. кількісна міра передавання енергії за допомогою впорядкованого руху частинок системи. 3. повна енергія частинок , що становлять певну речовину 4. функція стану термодинамічної системи характеризує стан хаосу в системі 5. енергія поступового руху молекул в системі 6. Теплоємність питома це це 1. кількість теплоти, яку необхідно надати 1 молю речовині , щоб нагріти її на 1 градус; 2. кількісна міра передавання енергії за допомогою впорядкованого руху частинок системи. 3. повна енергія частинок , що становлять певну речовину ; 4. функція стану термодинамічної системи характеризує стан хаосу в системі; 5. кількість теплоти, яку необхідно надати речовині масою 1 кг (г), щоб нагріти її на 1 градус . 7. Формула першого закону термодинаміки: 1. q=dU+W. 2. С=q/T . 3.Cv=dU/dT . 4. Cp=dH/dT. 5. S = KlnW. 8. Тепловий ефект хімічної реакції це … 1. кількість теплоти, виділена або увібрана в термодинамічною системою, коли єдиною роботою є робота розширення, а температура продуктів дорівнює температурі вихідних речовин. 2. 128 кількісна міра передавання енергії за допомогою впорядкованого руху частинок системи. 3. кількісна міра передавання енергії за допомогою хаотичного руху частинок системи. 4. функція стану термодинамічної системи характеризує стан хаосу в системі 5. повна енергія частинок , що становлять певну речовину; 9. Для ендотермічних реакцій тепловий ефект 1. ∆HT<0 ; 2. ∆HT =100 кДж. 10. ∆HT>0 ; 3. ∆HT=0 ; 4. ∆HT =273 кДж; 5. Фаза це … 1. Сукукпність усіх однорідних частин системи, що мають однакові властивості і відокремлені від інших частин системи поверхнею поділу. 2. сукупність тіл, що знаходяться у взаємодії і фактично або уявно виділені з навколишнього середовища. 3. сукупність тіл, які з навколишнім середовищем не обмінюються масою; 4. сукупність тіл, які обмінюються з навколишнім середовищем масою . 5. Параметр, який описує будь-яку властивісь системи и не залежить від способу досягнення даного стану. 11. Суміш олії та води складається з … 1. П’яти фаз. фаз. 12. 2. чотирьох фаз . 3. трех фаз. 4. одної фази. 5. двух Гетерогенна хімічна реакція – це реакція … 1. яка відбувається в одну стадію; 2. яка відбувається в кілька стадій; 3. яка закінчується при досягненні стану рівноваги; 4. у якої реагенти перебувають у різних фазових станах; 5. у якої реагенти перебувають у одному фазовому стані . 13. Визначте роботу ізобарного оборотного розширення N моль ідеального газу від температури Т1 до Т2. Відповідь дайте в кДж/моль. R=8.3 Дж/(моль*К). Дано: N=10 моль. Т1=298 К; Т2=398 К. 14. Скільки теплоти виділиться при згорянні M г графіту з утворенням СO2? Дано: M=24 г. ∆ Н = -393,5 кДж/моль. 129 15. При синтезі амміака N + 3H = 2NH рівноважні концетрації 2 2 3 речовин (моль/л) дорівнюють C(N2)=2.5; C(H2)=1.8; C(NH3)=3,6. Розрахуйте константу рівноваги цієї реакції? 16. У скільки разів збільшиться швидкість реакції при підвищенні температури від 50 до 70 С, якщо в даному температурному інтервалі температурний коефіцієнт швидкості реакції дорівнює 3? 17. Визначте роботу адіабатного оборотного розширення N моль ідеального газу від температури Т1 до Т2. Відповідь дайте в кДж/моль. R=8.3 Дж/(моль*К). Дано: N=10 моль. Т1=297 К; Т2=397 К; СP=18.3 Дж/(моль*К). 18. Скільки теплоти виділиться внаслідок згоряння сірки масою 240 г, якщо відомо, що зміна ентальпії реакції утворення оксиду сірки (ІV) з кисню і сірки становить – 297 кДж/моль? 130 Диханов С.М., Цикало А.Л. ФІЗИЧНА ХІМІЯ (Хімічна термодинаміка , Фізико-хімічний аналіз, Кінетика) Навчальний посібник Підписано до друку р. Формат . Умовн. друк. арк. , . Наклад прим. Надруковано видавницьким центром ОДАХ. 65082, Одеса, вул. Дворянська, 1/3 131 132