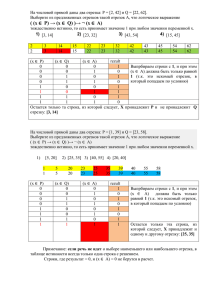
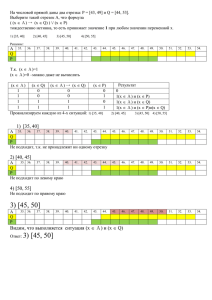
Задание 18. Числовая плоскость 1. Для какого наибольшего целого числа А формула ((x ≤ 9) →(x ⋅ x ≤ A)) ⋀ ((y ⋅ y ≤ A) → (y ≤ 9)) тождественно истинна, то есть принимает значение 1 при любых целых неотрицательных x и y? Решение. Раскроем импликацию по правилу A → B = ¬A + B Переменные не связаны между собой, поэтому необходимо и достаточно, чтобы: решениями первой совокупности были все неотрицательные х, решениями второй совокупности были все неотрицательные y. х > 9 , x2 A Решение неравенства х > 9 : числа 10, 11, 12, ... Не покрыт интервал 0..9 Чтобы совокупность выполнялась для всех целых неотрицательных чисел, числа 0, 1, 2, ... 9 должны быть решениями неравенства . Значит, максимальное х будет покрыто в результате неравенства: x2 A 92 A, А81 Самостоятельно для 2 совокупности неравенств Получим: 102>A, A < 100 81 A < 100 Искомое наибольшее целое значение параметра равно 99. Ответ: 99 2. Сколько существует целых значений числа A, при которых формула ((x < A) → (x2 < 81)) ∧ ((y2 ≤ 36) → (y ≤ A)) тождественно истинна при любых целых неотрицательных x и y? Решение. Раскроем импликацию по правилу A → B = ¬A + B будет иметь решения для любых целых неотрицательных чисел. Переменные не связаны между собой, поэтому необходимо и достаточно, чтобы: решениями первой совокупности были все неотрицательные х, решениями второй совокупности были все неотрицательные y. х2 < 81 , x A Решениями неравенства х2 < 81 являются числа из отрезка [0; 8]. Не покрыто множество [9; ) Значит, здесь будет выполняться 2 неравенство Чтобы совокупность выполнялась для всех целых неотрицательных чисел, числа из этого множества должны быть решениями. Значит, Любое число [0; 9] (9 включаем, тк неравенство x A нестрогое!) может быть значение параметра А. Самостоятельно, для 2й системы неравенств. Получим: А любое число из интервала [6; ) Найдем пересечение этих интервалов: [0; 9] [6; ) = [6 ; 9]. Возможных решений 4: это 6,7,8,9. Ответ: 4 3. На числовой прямой задан отрезок A. Известно, что формула ((x ∈ A) → (x2 ≤ 81)) ∧ ((y2 ≤ 36) → (y ∈ A)) тождественно истинна при любых вещественных x и y. Какую наименьшую длину может иметь отрезок A? Решение. Раскроем импликацию по правилу A → B = ¬A + B будет иметь решения для любых вещественных чисел. Переменные не связаны между собой, поэтому необходимо и достаточно, чтобы: решениями первой совокупности были все неотрицательные х, решениями второй совокупности были все неотрицательные y. Модуль числа! Решениями неравенства x2 ≤ 81 являются все числа из отрезка [−9; 9]. Чтобы совокупность выполнялась для всех вещественных чисел, числа x, не лежащие на указанном отрезке, должны принадлежать отрезку A. Следовательно, отрезок A не должен выходить за пределы отрезка [−9; 9]. Аналогично, решениями неравенства y2 ≤ 36 являются числа из множества ((- ; -6) ( 6; +)) Чтобы совокупность выполнялась для всех вещественных чисел, числа x, не лежащие на указанных лучах, должны лежать на отрезке A. Таким образом, минимальным отрезком из [−9; 9] и [−6; 6] будет отрезок [−6; 6]. Найдем его длину: 6 – (- 6 ) = 12 Наименьшая длина отрезка A может быть равна 12. О т в е т : 12. Самостоятельный разбор. 1. На числовой прямой задан отрезок A. Известно, что формула ((x ∈ A) → (x2 ≤ 100)) ∧ ((x2 ≤ 64) → (x ∈ A)) тождественно истинна при любом вещественном x. Какую наибольшую длину может иметь отрезок A? Ответ: 20 2. Сколько существует целых значений числа A, при которых формула ((x < 5) → (x2 < A)) /\ ((y2 ≤ A) → (y ≤ 5)) тождественно истинна при любых целых неотрицательных x и y? Ответ: 19 3. Сколько существует целых значений числа A, при которых формула ((x < 6) → (x2 < A)) ∧ ((y2 ≤ A) → (y ≤ 6)) тождественно истинна при любых целых неотрицательных x и y? Ответ: 23 4. Для какого наименьшего целого значения числа A выражение (x +2y < A) (y > x) (x > y ) тождественно истинно при любых целых неотрицательных x и y? Ответ: 91 Множества 1. На числовой прямой даны два отрезка: P = [37; 60] и Q = [40; 77]. Укажите наименьшую возможную длину такого отрезка A, что выражение (x ∈ P) → (((x ∈ Q) ∧ ¬(x ∈ A)) → ¬(x ∈ P)) истинно при любом значении переменной х. Обозначим: P = (x ∈ P), Q = (x ∈ Q), A = (x ∈ A). Перепишем логическое выражение и применим правила (импликация, закон де Моргана). Получим P (Q⋅(A P) = P + (Q ⋅A P) = =P + Q + A+ P = A +P + Q Отрезок [40; 60], его длина = 20. Ответ: 20