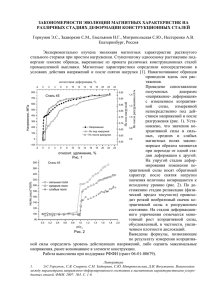
1. Введение и основные понятия
Сопротивление материалов – наука о прочности, жесткости и надежности элементов
инженерных конструкций. Методами сопротивления материалов ведутся
практические расчеты и определяются размеры деталей машин, различных
конструкций
и
сооружений.
Основные понятия сопротивления материалов опираются на законы и теоремы общей
механики
и
в
первую
очередь
на
законы
статики.
сопротивление
материалов
рассматривает
задачи,
c твердыми деформированными телами с изучением их физических свойств.
основные понятия:
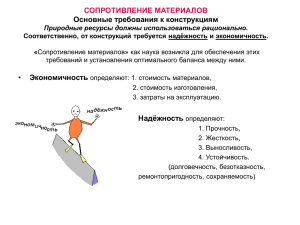
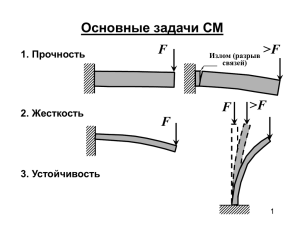
Прочность – это способность конструкции выдерживать заданную нагрузку, не
разрушаясь.
Жесткость – способность конструкции к деформированию в соответствие с заданным
нормативным регламентом.
Деформирование – свойство конструкции изменять свои геометрические размеры и
форму под действием внешних сил
Устойчивость – свойство конструкции сохранять при действии внешних сил
заданную форму равновесия.
Надежность – свойство конструкции выполнять заданные функции, сохраняя свои
эксплуатационные показатели в определенных нормативных пределах в течение
требуемого промежутка времени.
Ресурс – допустимый срок службы изделия. Указывается в виде общего времени
наработки или числа циклов нагружения конструкции.
Отказ – нарушение работоспособности конструкции.
Прочностной надежностью называется отсутствие отказов, связанных с разрушением
или недопустимыми деформациями элементов конструкции.
Упругостью называется свойство тела восстанавливать свою форму после снятия
внешних нагрузок.
Пластичностью называется свойство тела сохранять после прекращения действия
нагрузки, или частично полученную при нагружении, деформацию.
Ползучестью называется свойство тела увеличивать деформацию при постоянных
внешних нагрузках.
Основными моделями формы в моделях прочностной надежности являются: стержни,
пластины, оболочки и пространственные тела .
Модели
Основные модели формы в моделях прочностной надежности:
а) стержень, б) пластина, в) оболочка
Внешние силы, действующие на элемент конструкции, подразделяются на 3 группы:
1) сосредоточенные силы, 2) распределенные силы, 3) объемные или массовые силы.
Сосредоточенные силы — силы, действующие на небольших участках поверхности
детали
Распределенные силы приложены значительным участкам поверхности
Объемные или массовые силы приложены каждой частице материала
Обычно рассматриваются в зависимости от условий нагружения четыре модели
разрушения:
статического разрушения,
длительно статического разрушения,
малоциклового статического разрушения,
усталостного разрушения.
При малом числе циклов (N<102) развиваются значительные пластические
деформации (статическое разрушение), при большом числе циклов (N>10 5)
пластические деформации отсутствуют (усталостное разрушение). В промежуточной
области (102<N<105) разрушение носит смешанный характер (малоцикловое
разрушение). Если на элемент конструкции действует высокая температура (для
алюминиевых сплавов свыше 200 Co, для стальных и титановых сплавов свыше 400 Co,
для жаропрочных сплавов свыше 600 Co), но в этом случае рассматривается так
называемая
длительная
прочность
материала.
Таким образом, сопротивление материалов зависит не только от величин
действующего усилия, но и от длительности самого воздействия.
2. Метод сечений для определения внутренних усилий
Деформации рассматриваемого тела возникают от приложения внешней силы. При
этом изменяются расстояния между частицами тела, что в свою очередь приводит к
изменению сил взаимного притяжения между ними. Отсюда, как следствие, возникают
внутренние усилия. При этом внутренние усилия определяются универсальным
методом сечений или метод разреза.
различают силы внешние и внутренние. Внешние усилия (нагрузки) – это
количественная мера взаимодействия двух различных тел. К ним относятся и реакции
в связях. Внутренние усилия – это количественная мера взаимодействия двух частей
одного тела, расположенных по разные стороны сечения и вызванные действием
внешних усилий. Внутренние усилия возникают непосредственно в деформируемом
теле
Расчетная схема бруса с произвольной комбинацией внешней нагрузки образующую
равновесную систему сил:
(1)
При этом, реакции связей определяются из известных уравнений равновесия статики
твердого тела:
(2)
где х0, у0, z0 — базовая система координат осей.
Мысленное разрезание бруса на две части произвольным сечением А, приводит к
условиям равновесия каждой из двух отсеченных частей. Здесь {S’} и {S"}- внутренние
усилия, возникающих соответственно в левой и правой отсеченных частях вследствие
действия внешних усилий.
условие равновесия тела обеспечивается соотношением:
Так как исходная система внешних сил (1) эквивалентна нулю, получаем:
{S’} = – {S”}
(3)
Это условие соответствует четвертой аксиоме статики о равенстве сил действия и
противодействия.
Используя общую методологию теоремы Пуансо о приведении произвольной системы
сил к заданному центру и выбрав за полюс приведения центр масс,
сечения А', точку С', систему внутренних усилий для левой части {S’} сводим к
главному вектору 𝑅̅ʹ и главному моменту ̅̅̅
𝐿ʹ0 внутренних усилий. Аналогично делается
для правой отсеченной части, где положение центра масс сечения А”; определяется,
соответственно, точкой С" (рис.1 б,в).
{S’} ~ {R’,L’0}; {S"} ~ { R”,L”0},
(4)
R’ = – R”
(5)
’
”
L0=–L 0
Таким образом главный вектор и главный момент системы внутренних усилий,
возникающие в левой, условно отсеченной части бруса, равны по величине и
противоположны по направлению главному вектору и главному моменту системы
внутренних усилий, возникающих в правой условно отсеченной части.
последовательность действий (кроме п.1) составляет суть метода сечений (разреза),
единственного
метода
для
определения
внутренних
усилий.
1. Определите реакции в связях по величине и направлению в базовой системе
координат.
2. Определите количество участков бруса для использования метода сечений.
3. Мысленно рассеките брус в пределах исследуемого участка и изобразите на
Ваше усмотрение левую или правую условно отсеченную часть.
4. Укажите пределы изменения положения сечения вдоль продольной оси в
базовой системе координат на этом участке.
5. Введите в искомом сечении соответственно левую или правую следящую
систему координатных осей.
6. Задайтесь положительными направлениями внутренних усилий в следящей
системе координат.
7. Составьте уравнения равновесия для рассматриваемой условно отсеченной
части бруса в следящей системе координат.
8. Определите из уравнений равновесия искомые внутренние усилия.
9. Вычислите искомые внутренние усилия на границах участков и при
необходимости, — их экстремальные значения.
10.Выбрав масштаб усилий, выполните построение эпюры в соответствие с
полученными их модульными значениями и знаками.
3. Понятие о напряжениях и деформациях
Как отмечалось выше, внутренние силы, действующие в некотором сечении со
стороны отброшенной части тела, можно привести к главному вектору и главному
моменту. При уменьшении размеров площадки соответственно уменьшаются главный
вектор и главный момент внутренних сил, причем главный момент уменьшается в
большей степени. В пределе при ∆𝐹 → 0 получим
Аналогичный предел для главного момента равен нулю. Введенный таким образом
вектор рn называется вектором напряжений в точке. Этот вектор зависит не только от
действующих на тело внешних сил и координат рассматриваемой точки, но и от
ориентации в пространстве площадки ∆F, характеризуемой вектором п. Совокупность
всех векторов напряжений в точке М для всевозможных направлений
вектора п определяет напряженное состояние в этой точке.
В общем случае направление вектора напряжений рn не совпадает с направлением
вектора нормали п. Проекция вектора рn на направление вектора п называется
нормальным напряжением 𝜎𝑛1 , а проекция на плоскость, проходящую через точку М
и ортогональную вектору n, — касательным напряжением 𝜏𝑛 . Размерность
напряжений равна отношению размерности силы к размерности площади. В
международной системе единиц СИ напряжения измеряются в паскалях: 1 Па=1 Н/м2.
При действии внешних сил наряду с возникновением напряжений происходит
изменение объема тела и его формы, т. е. тело деформируется.
При этом различают начальное (недеформированное) и конечное (деформированное)
состояния тела.
Перемещение, при котором взаимное расположение точек тела не меняется, не
сопровождается деформациями.
Деформации тела характеризуются изменением взаимного расположения точек тела
до и после деформации. Предел отношения
называется относительной линейной деформацией в точке М в направлении вектора s,
При ∆𝑆1 → 0, ∆𝑆 → 0 изменение угла 𝛾12 между двумя ортогональными до деформации
направлениями называется угловой деформацией.
угловая деформация складывается из двух углов 𝛼1 и 𝛼2 , Если заданы три взаимно
ортогональных вектора, направленных вдоль координатных осей, то имеются три
угловые деформации 𝛾𝑥𝑦 , 𝛾𝑥𝑧 и 𝛾𝑦𝑧 , которые вместе с тремя линейными
деформациями 𝜀𝑥 , 𝜀𝑦 , 𝜀𝑧 полностью определяют деформированное состояние в точке.
4. Свойства тензора напряжений. Главные напряжения
Тензор напряжений обладает свойством симметрии. Так как тело находится в
равновесии, следовательно, находится в равновесии любая его часть, в том числе и
элементарный объем. Запишем одно из шести уравнений равновесия этого объема, а
именно — сумму моментов всех сил относительно оси Ох. Все силы, кроме двух, либо
не создают момента относительно ocи Ох, либо взаимно уничтожаются. Отличные от
нуля моменты создают компоненты 𝜏𝑦𝑧 (верхняя грань) и 𝜏𝑧𝑦 (права грань):
После сокращения на элемент объема dV=dxdydz получим
Аналогично, приравнивая нулю сумму
осей Оу и Ог, получим еще два соотношения
моментов
всех
сил
относительно
Эти условия симметрии и тензора напряжений называются также
условиями парности касательных напряжений: касательные напряжения,
действующие по двум взаимно перпендикулярным площадкам в направлениях,
ортогональных ребру, образованному пересечением этих площадок, равны по
величине. С учетом этих свойств из девяти компонент тензора напряжений
независимыми оказываются шесть компонент.
компоненты тензора напряжений определенные для трех взаимно перпендикулярных
площадок, полностью характеризуют напряженное состояние в точке, т. е. позволяют
вычислить компоненты вектора напряжений на площадках, произвольно
ориентированных относительно выбранной системы координат.
Главные напряжения обладают важным свойством: по сравнению со всеми другими
площадками нормальные напряжения на главных площадках принимают
экстремальные значения.
Три главные площадки, соответствующие главным напряжениям 𝜎1 , 𝜎2 , 𝜎3 , взаимно
перпендикулярны или, что то же самое, векторы nj и nk, соответствующие различным
значениям j и k —; ортогональны. Условие ортогональности имеет вид
Термин «инвариантность» обозначает независимость некоторой величины от выбора
системы координат.
Введем среднее напряжение по формуле
Тензор напряжений можно представить в виде суммы двух тензоров
𝜎̃ = 𝑠̃ + 𝑑̃ , где
Первый тензор называется шаровым, он характеризует изменение объема тела без
изменения его формы. Второй тензор, называемый девиатором, характеризует
изменение формы. Особенностью девиатора напряжений является равенство нулю его
первого инварианта:
Найдем положение площадок, на которых касательные напряжения принимают
экстремальные значения. Для этого нужно отыскать экстремумы касательного
напряжения. Экстремальные касательные напряжения
действуют на площадках, параллельных одной из главных осей и образующих с двумя
другими осями угол
.
№ 5. Упругость и пластичность. Закон Гука
Действие внешних сил на твердое тело приводит к возникновению в точках его
объема напряжений и деформаций. При этом напряженное состояние в точке, связь
между напряжениями на различных площадках, проходящих через эту точку,
определяются уравнениями статики и не зависят от физических свойств материала.
Деформированное состояние, связь между перемещениями и деформациями
устанавливаются с привлечением геометрических или кинематических соображений
и также не зависят от свойств материала.
Наиболее распространенными для конструкционных материалов являются модели
упругости и пластичности. Упругость — это свойство тела изменять форму и
размеры под действием внешних нагрузок и восстанавливать исходную
конфигурацию при снятии нагрузок.
При высоких уровнях нагружения, когда в теле возникают значительные
деформации, материал частично теряет упругие свойства: при разгрузке его
первоначальные размеры и форма полностью не восстанавливаются, а при полном
снятии внешних нагрузок фиксируются остаточные деформации. В этом
случае зависимость между напряжениями и деформациями перестает быть
однозначной. Это свойство материала называется пластичностью.
Накапливаемые в процессе пластического деформирования остаточные деформации
называются пластическими.
Пусть материал является линейно-упругим и изотропным.
При таком нагружении происходит увеличение размеров в направлении
оси Ох, характеризуемое линейной деформацией
, которая пропорциональна
величине напряжения
(1)
Это соотношение является математической записью закона
Гука, устанавливающего пропорциональную зависимость между напряжением и
соответствующей линейной деформацией при одноосном напряженном
состоянии. Коэффициент пропорциональности E называется модулем продольной
упругости или модулем Юнга. Он имеет размерность напряжений.
(5)
Касательные напряжения вызывают угловые деформации, причем при малых
деформациях они не влияют на изменение линейных размеров, и следовательно, на
линейные деформации. Поэтому они справедливы также в случае произвольного
напряженного состояния и выражают так называемый обобщенный закон Гука.
(6)
которые выражают закон Гука при сдвиге. Коэффициент пропорциональности G
называется модулем сдвига.
6. Механические характеристики конструкционных
материалов
Механические характеристики определяются следующими факторами:
веществом, его структурой и свойствами;
конструктивными особенностями элемента, т. е, размерами, формой, наличием
концетраторов, состоянием поверхности;
условиями при нагружении: температурой, скоростью, повторяемостью
нагрузки и др.
Конструкционные материалы в процессе деформирования вплоть до разрушения
ведут себя по разному. Пластичное поведение характеризуется существенным
изменением формы и размеров, при этом к моменту разрушения развиваются
значительные деформации, не исчезающие после снятия нагрузки. Такие материалы
называют пластичными. При хрупком поведении разрушение наступает при весьма
малых деформациях, и материалы с такими свойствами называют хрупкими. Однако
одни и те же конструкционные материалы, находящиеся в различных условиях
деформирования, ведут себя по разному: при одних условиях проявляют себя как
пластичные материалы, при других—как хрупкие. В связи с этим, основные
макромеханические характеристики материалов — упругость, пластичность, вязкость
и др. правильнее относить не к их свойствам, а к состояниям материала.
В упругом состоянии деформации обратимы, и вся энергия, затраченная на
деформирование, при разгрузке возвращается (диссипация энергии отсутствует). Для
любого твердого тела процесс деформирования начинается с упругой деформации.
Изотропное тело имеет две константы упругости— модуль упругости
Е и коэффициент Пуассона 𝜇 . Для анизотропных тел число упругих констант в
общем случае равно 21. Из основных констант упругости можно получить их
производные—модуль сдвига G, модуль объемной реформации К и постоянную Ламе
𝜆 . Вязкое сопротивление — в некотором смысле противоположно упругому —
работа внешних сил, уравновешенных силами вязкого сопротивления, полностью
рассеивается в виде тепла.
Высокоэластическое состояние — наиболее характерно для полимеров;
особенностями этого состояния являются большая изменяемость формы и
деформирование без изменения объема.
. Состояние разрушения — состояние, при котором за счет интенсивного развития
трещин в материале тела начинается нарушение его сплошности и непрерывности.
Основным опытом для определения механических характеристик конструкционных
материалов является опыт на растяжение призматического образца центрально
приложенной силой, направленной по продольной оси; при этом в средней части
образца реализуется однородное напряженное состояние. Форма, размеры образца и
методика проведения испытаний определяются соответствующими стандартами,
например, ГОСТ 34643—81, ГОСТ 1497-73.
У многих конструкционных материалов площадка текучести не выражена столь явно,
как у малоуглеродистых сталей. Для таких материалов вводится понятие условного
предела текучести ; это напряжение, которому соответствует остаточная
(пластическая) деформация, равная 0,2%. После площадки текучести для
дальнейшего увеличения деформации необходимо увеличение растягивающей силы.
. Хрупкие материалы проявляют значительно лучшую способность сопротивляться
деформациям сжатия, чем деформациям растяжения; для них разрушающее
напряжение при сжатии превышает предел прочности при растяжении в несколько
раз. Разрушение хрупких материалов при сжатии происходит за счет образования
трещин.
7. Влияние различных факторов на механические
характеристики материалов
Зависимость механических характеристик конструкционных материалов от их
химического состава, внешних условий и условий нагружения весьма многообразна;.
Влияние содержания углерода- Введение различных легирующих добавок в
металлы позволяет значительно повысить прочностные характеристики сплавов
Влияние температуры окружающей среды. - Повышенные температуры
оказывают существенное влияние на такие механические характеристики
конструкционных материалов, как ползучесть и длительная
прочность. Ползучестью называют медленное непрерывное возрастание
пластической (остаточной) деформации под воздействием постоянных
нагрузок. Длительной прочностью называется зависимость разрушающих
напряжений (временного сопротивления) от длительности эксплуатации. Свойства
ползучести и длительной прочности проявляются у углеродистых сталей при Т
>300oС, для легированных сталей при Т>350oС. для алюминиевых сплавов при
Т>100oС.
предел ползучести — напряжение, при котором пластическая деформация за
определенный промежуток времени достигает заданной величины. Ползучесть
сопровождается релаксацией напряжений — самопроизвольным уменьшением
напряжений с течением времени при неизменной деформации. Скорость релаксации
напряжений возрастает при повышении температуры. Мерой скорости релаксации
служит время релаксации—промежуток времени, в течение которого напряжение
уменьшается по сравнению с начальным значением в е=2,718 раза. Прочность
материала при повышенных температурах оценивается пределом длительной
прочности — напряжением, при котором материал разрушается не ранее заданного
времени.
Влияние температур на упругие свойства. Температурный коэффициент
линейного расширения
упругости
и температурный коэффициент модуля
связаны между собой соотношением
или
где r и m — постоянные, характеризующие параметры
кристаллической решетки. Для сталей с повышением температуры испытаний с 25 до
450oС модули упругости Е и G уменьшаются на 20—40%, при этом, начиная с 300—
400oС наблюдается расхождение между значениями модулей, определенными при
статических и динамических испытаниях. Изменение модулей упругости при малый
колебаниях температуры (от –50 до +50oС) незначительно и им обычно
пренебрегают.
8.
НАПРЯЖЕНИЯ ПРИ РАСТЯЖЕНИИ (СЖАТИИ) ПРИЗМАТИЧЕСКИХ
СТЕРЖНЕЙ. РАСЧЕТ НА ПРОЧНОСТЬ
Стержни постоянного поперечного сечения с прямолинейной осью призматические стержни. деформация растяжения -сжатия. под растяжением
(сжатием) понимают такой вид деформации стержня, при котором в его поперечном
сечении возникает лишь один внутренний силовой фактор — продольная
сила Nz. Поскольку продольная сила численно равна сумме проекций, приложенных к
одной из отсеченных частей внешних сил на ось стержня (для прямолинейного
стержня она совпадает в каждом сечении с осью Oz), то растяжение (сжатие) имеет
место, если все внешние силы, действующие по одну сторону от данного
поперечного сечения, сводятся к равнодействующей, направленной вдоль оси
стержня . Одна и та же продольная сила Nz при действии на различные части стержня
(левую или правую) имеет противоположные направления. Знак Nz зависит от
характера вызываемой ею деформации. Продольная сила считается положительной,
если вызывает растяжение элемента и она отрицательна, если вызывает сжатие .
Представим себе стержень, изготовленный из какого-либо податливого материала
на боковую поверхность которого нанесена система продольных и поперечных рисок
. Эта ортогональная система рисок остается таковой и после приложения
растягивающей нагрузки. Поскольку поперечные риски являются следами
поперечных сечений на поверхности стержня и остаются прямыми и
перпендикулярными к оси стержня то это свидетельствует о выполнении гипотезы
плоских сечений (Бернулли). С учетом гипотезы об отсутствии поперечного
взаимодействия продольных волокон приходим к выводу, что деформация
растяжения стержня сводится к одноосному растяжению его продольных волокон,
Ортогональность продольных и поперечных рисок свидетельствует также об
отсутствии сдвигов, а, следовательно, и связанных с ними касательных напряжений т
в поперечных и продольных сечениях стержня.
Тогда продольная сила Nz равная сумме проекции внутренних сил, действующих в
данном поперечном сечении площадью F очевидно будет равна
.
Таким образом, задача определения напряжений даже в самом простом случае
деформирования стержня (растяжении или сжатии) оказывается статически
неопределимой.
или
Таким образом, при растяжении (сжатии) призматического стержня нормальные
напряжения равномерно распределены по поперечному сечению, а касательные
напряжения в сечениях отсутствуют, что является следствием гипотезы плоских
сечений.