Учебная презентация (введение в сопротивление материалов)
реклама
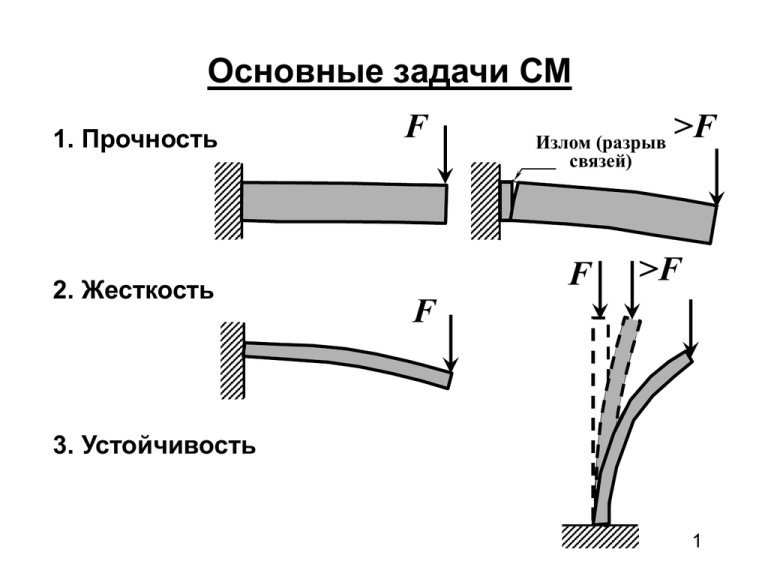
Основные задачи СМ 1. Прочность 2. Жесткость F Излом (разрыв связей) F >F >F F 3. Устойчивость 1 Типы элементов конструкций l b h d брус или стержень l >> d a пластинки h<a, h<b 2 Типы элементов конструкций h c R b a массивные тела abc оболочка h<<R 3 Основные гипотезы Сплошность – непрерывность пространства тела, хотя тела имеют дискретное (атомарное) строение. Однородность – независимость механических свойств от координат точек тела. Изотропность – одинаковость механических свойств во всех направлениях. Упругость – способность материала восстанавливать начальную форму и размеры после снятия нагрузки. Относительная жесткость – деформации и перемещения малы можно использовать ТМ для определения реакций опор и внутренних усилий 4 Классификация сил 1. Внешние и внутренние 2. Статические и динамические 3. Постоянные и временные 5 Метод сечений F3 z B Mz П F1 F3 Qz F4 F4 N A П F2 y Qy Mx My x 6 Метод сечений F1 DA – элементарная площадь F2 DF f cp – среднее напряжение DA DF – полное lim f напряжение на элем. DA площадке DA fср DF F f L 2 H ; 2 м Н 1 2 1Па; м 7 Метод сечений Разложим полное напряжение на составляющие: x y sx tyx tzx z sx DA t zx ,t yx – нормальное напряжение – касательные напряжение 8 Растяжение (сжатие) прямых стержней Деформацией растяжения (сжатия) прямого стержня называется такой случай сопротивления стержня, когда внутренние силы в его поперечном сечении сводятся (статически эквиваленты) к одной равнодействующей, направленной вдоль продольной оси стержня. Эта равнодействующая называется продольной силой. 9 F1 Растяжение (сжатие) прямых стержней F3 F2 Y y F1 = 20 кН F2 = 30 кН F3 = 25 кН X x A F1 F1 B I N 1 kx F M ky II F2 N 2 I MB F II II F3 N2 B 0; F1 F2 F3 X 0; 0; Y 0; 0; M B 0; X = F1 - F2 + F3 = 15 кН X II 20 15 + + - Эп N (кН) 10 10 Растяжение (сжатие) прямых стержней Важное правило знаков: Продольная растягивающая сила направляется от сечения и считается положительной. Правило: Продольная сила равна сумме проекций всех внешних сил, взятых по одну сторону от сечения, на продольную ось стержня с учетом правила знаков. 11 Напряжения и деформации F F Гипотеза Бернулли (гипотеза плоских сечений): Поперечные сечения при деформации не искривляется, т.е. остаются плоскими при растяжении-сжатии все продольные волокна удлиняются на оду и ту же величину. 12 Напряжения и деформации «до» деформации b b1 «после» деформации l Dl - удлинение стержня, Dl Db = b1 – b – сужение стержня Ведем относительные деформации: Dl l - продольная деформация Db b * - поперечная деформация 13 Напряжения и деформации Пуассон заметил: * - Const для каждого материала Коэффициент Пуассона – отношение относительной поперечной деформации к относительной продольной деформации при растяжении или сжатии стержня Для изотропных материалов: 0 0.5 Сталь: ~ 0.25 …0.3 Медь: ~ 0.4 Бетон: ~ 0.15 Резина: ~ 0.5 14 Напряжения и деформации В 1676 году Роберт Гук экспериментально установил sx = E E – модуль продольной упругости ([E] = МПа) Сталь: E ~ 2·105 МПа Медь: E ~ 1·105 МПа Бетон: E ~ 104 …105 МПа Алюминий: E ~ 7·104 МПа 15 Напряжения и деформации В поперечном сечении стержня: N s x DA A DА sx N N s x dA т.к.s x const s x A A N нормальное напряжение в поперечном сечении sx A стержня Nl Dl EA закон Гука для удлинения жесткость стержня при растяжении 16 Напряжения и деформации Условие прочности при растяжении: s max N max R A или [s ] R – расчетное сопротивление [s] – допускаемое напряжение 17








