Изотермы и изобары адсорбции. Уравнение Генри. Константа адсорбционного равновесия. Уравнение Лэнгмюра. Адсорбция из растворов. Уравнение Брунауэра – Эмета– Теллера (БЭТ) для полимолекулярной адсорбции. Определение площади поверхности адсорбента.
реклама

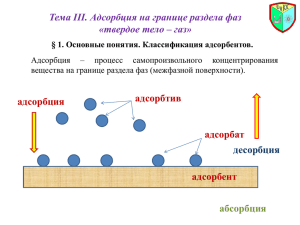
Государственное бюджетное образовательное учреждение высшего образования Московской области «Университет «Дубна» Реферат по теме: Изотермы и изобары адсорбции. Уравнение Генри. Константа адсорбционного равновесия. Уравнение Лэнгмюра. Адсорбция из растворов. Уравнение Брунауэра – Эмета– Теллера (БЭТ) для полимолекулярной адсорбции. Определение площади поверхности адсорбента. Аспирант Логунов А.И. Направление 04.04.01 «Физическая химия» Кафедра Химии, новых технологий и материалов Оглавление Введение .............................................................................................................................3 Изотермы и изобары адсорбции .......................................................................................4 Уравнение Генри................................................................................................................8 Константа адсорбционного равновесия...........................................................................9 Уравнение Лэнгмюра ......................................................................................................11 Уравнение Брунауэра – Эмета– Теллера (БЭТ) для полимолекулярной адсорбции 13 Использованная литература ............................................................................................18 Введение Адсорбция – как явление сопровождает двухфазные многокомпонентные системы. Адсорбция имеет место на границах раздела: газ – тв. тело, жидкость – тв. тело, жидкость – жидкость, газ – жидкость в отсутствии химического взаимодействия и растворения. Теплота адсорбции ∆Η = ∆G + T⋅∆S всегда отрицательна, так как ∆G и ∆S отрицательны при самопроизвольной адсорбции. Все адсорбционные процессы экзотермичны. Различают два вида адсорбции – физическая и химическая адсорбция. Физическая адсорбция вызвана Ван – дер – ваальсовыми силами взаимодействия между молекулами адсорбата и адсорбента. Эти силы невелики и поэтому теплота физической адсорбции составляет ~ 10 – 30 кДж/моль. Химическая адсорбция, или хемосорбция, обязана химической связи, возникающей между адсорбатом и адсорбентом. При этом образуются поверхностные соединения. Теплота хемосорбции составляет ~ 100 – 400 кДж/моль, а сам процесс хемосорбции носит активационный характер. Молекулы адсорбата и адсорбента должны обладать энергией, которая превышает некоторое пороговое значение (энергия активации). Энергетические характеристики этих двух видов адсорбции и обуславливают их основные отличия (см таблицу 1). Адсорбция характеризуется величиной Гi = ni/S , т. е. числом частиц ,адсорбированных на единицу поверхности. Твёрдые адсорбенты обладают развитой поверхностью, величина которой составляет 1 – 2000 м2/г. Если поверхность адсорбента неизвестна, то количество поглощённого газа относят к 1 см3 или к 1г адсорбента. Зависимость Г = f(P) или Г = f(C) при постоянной температуре называется изотермой адсорбции. Таблица 1. Основные различия между физической и химической адсорбцией[1]. Изотермы и изобары адсорбции Изотермы Сложность изучения адсорбции из растворов обусловлена воз - можностью сорбции всех компонентов, что влияет на характер изотермы адсорбции. Даже если раствор содержит одно растворённое вещество, то на его адсорбцию будет влиять растворитель, который может конкурировать за адсорбционные центры поверхности. Кроме того, возможны случаи разного характера взаимодей- ствия молекул адсорбирующегося вещества в растворе и на поверхности адсорбента, что также приводит к разнообразию изотерм адсорбции. Чарльз Гильс предложил разделить изотермы адсорбции на 4 класса (S, L, Н, С) по форме начального участка изотермы и на 5 типов по изменению формы кривой при более высоких концентрациях (рис. 1). Рисунок 1. Классификация изотерм адсорбции из растворов по Гильсу [2] Изотермы класса S имеют вогнутый начальный участок. При возрастании концентрации адсорбтива в растворе резко увеличивается адсорбционная ёмкость сорбента, что может быть связано с изменением ориентации адсорбированных молекул относительно поверхности сорбента (например, для ароматических соединений возможна параллельная и перпендикулярная ориентация бензольного кольца) или с быстрым переходом к полимолекулярной адсорбции. Далее часто следует точка перегиба и появляется второе плато (S2-S4), что придаёт таким изотермам характерный 8-образный вид. Причина - сильное взаимодействие между адсорбированными молекулами при одновременном ослаблении взаимодействия молекул адсорбтива с адсорбентом, что приводит, в целом, к увеличению теплоты адсорбции. В этом случае адсорбированные молекулы стремятся расположиться на поверхности в виде скоплений (цепей, кластеров и т. д.), чему способствует монофункциональный характер адсорбтива и сильная адсорбция растворителя, который в ряде случаев может вытеснять адсорбированное вещество. При этом на изотерме появляется максимум (S5). Этому способствует и изменение состояния растворённого вещества при достижении определённой концентрации его в растворе. Изотермами класса S описывается адсорбция ограниченно растворимых жидких веществ из воды, адсорбция фенола на оксиде алюминия из воды, адсорбция пнитрофенола на кремнеземе из бензола, насыщенного водой. При изучении адсорбции веществ из растворов довольно часто встречаются изотермы адсорбции класса L (изотермы Ленгмюра). Ими хорошо описывается, например, адсорбция метанола на триацетате целлюлозы или сухой целлюлозе из бензола, адсорбция глюкозы на графите из воды, адсорбция 1,4-нитрофенола из бензола на оксиде алюминия. Для изотерм класса L характерна независимость теплоты адсорбции от степени заполнения поверхности и отсутствие конкуренции со стороны растворителя. Для изотерм класса L характерен выгнутый относительно оси концентраций начальный участок, так как с увеличением доли занятых адсорбционных мест молекулам адсорбтива сложнее найти вакантное место, особенно если они склонны к образованию больших ассоциатов с повышением их концентрации в растворе за счёт межмолекулярного взаимодействия. Изотермы L2 характерны для случаев, когда при определённой концентрации адсорбтива адсорбция достигает предела. Если адсорбция продолжается и после заполнения монослоя, то возможны изотермы L3, которые при насыщении адсорбционного слоя и появлении второго плато переходят в изотермы L4. Это может быть обусловлено полимолекулярной адсорбцией или переориентацией молекул или их ассоциатов относительно поверхности сорбента. Наличие максимума на изотермах типа L5 возможно в результате какого-либо изменения, происходящего с растворённым веществом, например, при мицеллообразовании, или при наличии примесей высокоактивных веществ (например, ПАВ), находящихся в виде ассоциатов с молекулами адсорбтива. Изотермы класса Н в области низких концентраций имеют круто восходящий, практически вертикальный участок. Это возможно в случае большого сродства адсорбата к адсорбенту и чрезвычайно сильной адсорбции, которая может привести к образованию химических соединений на поверхности сорбента (хемосорбции). Часто изотермы класса Н являются следствием обмена между функциональными группами сорбента и ионами, образующимися при диссоциации адсорбтива в растворителе. Изотермы этого класса наблюдаются при адсорбции жирных кислот из бензола на никеле Ренея, при адсорбции стеариновой кислоты на натриевой селитре из бензола, при адсорбции хлорида додециламмония на оксиде алюминия из воды. Изотермы класса С отличаются линейным начальным участком, что соответствует сохранению числа адсорбционных центров в широком диапазоне концентраций вплоть до максимально возможной адсорбции адсорбтива из раствора. При этом может реализоваться случай, когда по мере заполнения одних центров появляются новые и доступная для адсорбции поверхность увеличивается пропорционально количеству адсорбированного из раствора веще - ства. Так, при адсорбции красителей на микропористых волокнистых материалах (полимерах) происходит увеличение поверхности адсорбента пропорционально количеству адсорбированного веще - ства (происходит раскрытие ранее недоступной поверхности - механизм замка на застежке «молния»). Условиями получения изотерм класса С являются наличие у пористого сорбента «гибких» слоев или областей с различной степенью кристалличности, высокое сродство адсорбирующегося вещества к сорбенту, большая проникающая способность адсорбти- ва и геометрия молекулы адсорбтива. Кроме того, изотермы класса С описывают адсорбцию вещества, распределённого между двумя несмешивающимися растворителями. Изобары Величина адсорбции компонента а может быть выражена как функция а = f(P,T, i ), где i -остальные параметры, которые для каждой конкретной пары адсорбент/адсорбат остаются постоянными и далее для упрощения могут не записываться. Величина а обычно выражается в мМоль (адсорбата)/г (адсорбента), в нсм3 адсорбированного газа/г адсорбента, см3жидкости/г адсорбента, может быть отнесена не к массе, а к поверхности адсорбента, объему слоя адсорбента и т.д. Изобара адсорбции - это зависимость равновесных величин адсорбции от температуры при постоянном давлении Р адсорбтива, т.е. зависимость а = f(Т)Т,i. Типичный вид изобар адсорбции показан на рис 1. Область насыщения соответствует полному заполнению всех пор. С повышением Т адсорбция обычно убывает. Рисунок 2. Изобара адсорбции для случая активированной адсорбции Обычно изобары адсорбции рассчитывают по ИА, измеренным при разных Т, хотя возможно и прямое их измерение. Связь между изотермами, изобарами и изотермами адсорбции следует из общего анализа уравнения а = f(P,T)i, рассматриваемого как непрерывная функция двух независимых аргументов Р и Т. Полный дифференциал этой функции равен da = a/P T dP + a/T P dT где член a/P T - производная изотермы адсорбции при температуре Т, а член a/TP - производная изобары адсорбции при давлении Р. Отметим, что это уравнение может быть использовано для расчета погрешностей измерений величин адсорбции а, обусловленных ошибками измерений Р и Т. Уравнение Генри При адсорбции из низкоконцентрированных растворов количество адсорбированного вещества прямо пропорционально содержа - нию адсорбтива в растворе. Следовательно, экспериментальная изотерма представляет собой прямую линию, выходящую из начала координат (кроме изотерм класса Н). Эти начальные участки хорошо описываются уравнением изотермы Генри: Г = КнС, где Г - величина адсорбции (моль/г), С - равновесная концентрация (моль/л) и Кн константа Генри (л/г), которая характеризует распределение вещества между адсорбентом и раствором. На её величину влияют температура и природа веществ, но она не зависит от концентрации адсорбтива. Закон Генри выполняется только при низких степенях заполнения поверхности адсорбатом, поэтому область его действия мала. Неоднородность поверхности и усиление взаимодействия между адсорбированными молекулами с увеличением заполнения поверхности приводит к отклонению от линейной зависимости. степени Константа адсорбционного равновесия Константа адсорбционного равновесия К, подобно константам равновесия реакций в газах или растворах, связана со стандартным изменением изохорного потенциала уравнением F0 =U0- T S0 = - RT ln K (1) откуда следует К =e S0/R e-U0/RT =g eQ/RT (2) где g- энтропийный множитель, Q- теплота адсорбции. Аналогично можно получить уравнение Ленгмюра при одновременной адсорбции смеси компонентов на одних и тех же центрах. Так, адсорбцию бинарной смеси газов А и В можно рассматривать как две параллельные реакции взаимодействия газов А и В со свободной поверхностью по схеме Ленгмюра, полагая, что молекулы А и В адсорбируются на одних и тех же свободных центрах: А(газ) + свободное место [Z] [ A Z ] и В(газ) + свободное место [Z] [ B Z ] где [ A Z ] и [ B Z ] - соответствующие поверхностные комплексы. Условия равновесия для каждого компонента аналогичны уравнению: КА = А/ PА [1 - А - В ) (3) КВ= В/ PВ [1 - А - В ) (4) Разделив (1) на (2), получим А/В = КА РА / КВ РВ (5) Далее подстановка выражения для В из (2.15) и простейшие преобразования дают А =КАРА/[1+ КАРА+ КВРВ] (6) Аналогично получается выражение для В. В общем случае адсорбции i компонентов получим выражение для степени покрытия поверхности компонентом i i =КiPi /[1+iКi Pi] (7) и суммарной степени покрытия поверхности всеми компонентами = I Кi Pi /[1+i Кi Pi ] (8) где Рi- парциальное давление компонента смеси i, Кi - его константа рав- новесия. Из уравнения (2.18.1) следует, что адсорбция каждого компонента смеси возрастает с увеличением его парциального давления Рi и убывает с ростом парциального давления других компонентов, это влияние усиливает-ся с ростом значений Кi для других компонентов. Уравнение Ленгмюра для хемосорбции, сопровождающейся диссоциацией молекул на два фрагмента, каждый из которых занимает один отдельный центр, записывается как =(кР)1/2 / [1+(КР) 1/2 ] (9) Дальнодействие сил при физической адсорбции обуславливает образование нескольких слоев адсорбированных молекул. Заполнение второго слоя маловероятно до тех пор, пока на поверхности находятся только отдельные изолированные молекулы, т.к. силы взаимодействия между единичной ад-сорбированной молекулой и ударяющейся о нее молекулой обычно малы по сравнению с силами на поверхности адсорбента, где в взаимодействии одновременно участвует большое число молекул. Но по мере увеличения поверхностной концентрации адсорбата возрастает вероятность одновременного взаимодействия ударяющейся молекулы адсорбтива с 3, 4 и более адсорбированными ранее молекулами. “Время жизни” возрастает до значений, при которых на отдельных участках поверхности может начи-наться полимолекулярная адсорбция. Уравнение Лэнгмюра Если на поверхности адсорбента может адсорбироваться только один слой молекул, то с ростом концентрации растворённого вещества происходит насыщение поверхности молекулами адсорбата (рис. 2). Данная теория мономолекулярной адсорбции была предложена американским химиком Ирвингом Ленгмюром и основывается на следующих допущениях: адсорбция локализована (молекулы не перемещаются по поверхности) на отдельных адсорбционных центрах, каждый из которых взаимодействует только с одной молекулой адсорбата; Б) адсорбционные центры энергетически эквивалентны - поверхность адсорбента эквипотенциальна; адсорбированные молекулы не взаимодействуют друг с дру- том; Г) при адсорбции происходит обратимая квазихимическая реакция между распределяемым компонентом и адсорбционными центрами поверхности. Уравнение Ленгмюра широко используют для описания экспериментальных изотерм адсорбции: где Г - величина адсорбции (моль/г), Гтах - ёмкость адсорбционного монослоя или максимальная величина адсорбции (моль/г), С - равновесная концентрация (моль/л), Со стандартная концентрация, равная 1 моль/л, Кл - константа равновесия процесса взаимодействия адсорбата с адсорбентом (константа Ленгмюра). Линейная форма уравнения Ленгмюра удобна для анализа экспериментальных изотерм адсорбции: Используя полученные значения Гтсх и Кл, можно вычислить максимальный объём (Vо) адсорбированного вещества, стандартную энергию Гиббса адсорбции ( площадь (ω), которую занимает одна молекула адсорбата («посадочная площадка»): ) и где М - молярная масса вещества (г/моль), р - плотность вещества (г/см3), R универсальная газовая постоянная (8,3143 Дж/моль·К), Т - температура (К), АУД - удельная поверхность сорбента (м2/г), NА - число Авогадро (6,022·1023 1/моль). Если Кд·(С/С0) << 1, то уравнение Ленгмюра переходит в уравнение Генри. Использование уравнений Генри и Ленгмюра справедливо только для описания изотерм адсорбции, в случае адсорбентов с энергетически эквивалентными адсорбционными центрами. Уравнение Брунауэра – Эмета– Теллера (БЭТ) для полимолекулярной адсорбции Физическая адсорбция газов непористыми твердыми телами в большинстве случаев описывается изотермами адсорбции II типа. В принципе из такой изотермы адсорбции, полученной для данного газа на определенном образце твердого тела, можно определить емкость монослоя для этого образца, которую в свою очередь можно использовать для вычисления его удельной поверхности. Емкость монослоя определена как количество адсорбата, которое можно определенным образом разместить в полностью заполненном адсорбционном слое толщиной в одну молекулу – монослое – на поверхности единицы массы (1 г) твердого тела. Из емкости монослоя nm (выраженной в молях адсорбата) в расчете на грамм адсорбента удельная поверхность S как поверхность 1 г твердого тела вычисляется по простому уравнению: S = nmsmNA где sm – средняя площадь, занимаемая молекулой адсорбата в заполненном монослое. Если адсорбированное количество выражено в других единицах, вводится соответствующий коэффициент. Так, если адсорбция выражена в граммах, а sm в нм2 на одну молекулу, то S = (xm/M)smNA·10-18 где M – молекулярная масса адсорбата, xm – емкость монослоя в граммах на грамм твердого тела, S – удельная поверхность в квадратных метрах на грамм. Если емкость монослоя vm выражена в виде объема газа при нормальных условиях (мл/г), то удельная поверхность составит: S = (vm/22414)smNA·10-18 м2/г Чтобы получить величину емкости монослоя из изотермы, необходимо дать количественную интерпретацию последней. Ни одна из теорий, выдвинутых в разное время, не решает эту задачу полностью. Наиболее успешной и наиболее известной попыткой является теория Брунауэра, Эммета, Теллера. Хотя она основана на очень простой модели и поэтому неоднократно критиковалась, выдвинутое этими авторами уравнение, так называемое уравнение БЭТ, привело к замечательному успеху в определении удельной поверхности из изотерм адсорбции II типа. Так как в реальных случаях адсорбции допущения, на которых основана теория Ленгмюра, зачастую не выполняются строго, то реальные изотермы адсорбции более или менее сильно отклоняются от ленгмюровской изотермы. Поэтому в последующие годы различные авторы развивали теорию изотермы адсорбции, ослабляя категоричность постулатов, лежащих в основе классической модели Ленгмюра [3]: Во-первых, адсорбция не всегда строго локализована. Во-вторых, поверхность твердого тела энергетически не вполне однородна, адсорбционные центры неравноценны. Еще сам Ленгмюр показал, как изменится уравнение изотермы, если считать адсорбционные центры энергетически неоднородными (рис. 7.12). В-третьих, всегда имеет место взаимодействие адсорбированных молекул между собой. Рисунок 3. Адсорбционные центры с разной энергией В этом случае уравнению Ленгмюра будет подчиняться адсорбция для каждой группы одинаковых по энергии центров: В этом уравнении подстрочные символы 1, 2, 3,..., i относятся к разным группам одинаковых по энергии центров. Р. Фаулер и Э. Гугенгейм, а также Я. де Бур и Т. Хилл получили уравнения изотермы адсорбции, в которых учитываются тангенциальные взаимодействия адсорбированных молекул. Наконец, С. Брунауэр, П. Эммет и Э. Теллер отказались от допущения Ленгмюра, приводящего к мономолекулярной адсорбции. Эти авторы разработали теорию полимолекулярной адсорбции, называемую теорией БЭТ, по начальным буквам фамилий ее авторов. Теория БЭТ описывает все пять видов изотерм адсорбции. Основные положения теории БЭТ следующие: • молекулы первого слоя адсорбируются на поверхности адсорбента в результате межмолекулярного взаимодействия адсорбент — адсорбат; • каждая адсорбированная молекула первого адсорбционного слоя может являться вторичным центром адсорбции для молекул второго слоя, а те в свою очередь — молекул третьего и т.д. (формируются второй и последующие адсорбционные слои). Адсорбция считается полислойной; • теплота адсорбции в первом слое определяется взаимодействием адсорбат — адсорбент, во всех последующих слоях — взаимодействием адсорбат — адсорбат. Поэтому теплота адсорбции во всех слоях, начиная со второго, равна теплоте конденсации; • начало образования второго и последующих слоев возможно и при незаконченном первом (рис. 3). • каждый адсорбционный слой находится в динамическом равновесии с окружающей средой и соседними слоями. Теория БЭТ сохраняет ленг- мюровскую концепцию о динамическом характере адсорбции. Рисунок 4. Модель адсорбционного слоя по теории БЭТ Составив уравнение адсорбционного равновесия для каждого слоя и просуммировав их, авторы теории получили уравнение изотермы адсорбции (основное уравнение теории БЭТ): где Р/Р$ — относительное давление пара адсорбгива (Ps — давление насыщенного пара при данной температуре); ат — величина адсорбции при мо- нослойном заполнении поверхности, г.е. емкость монослоя (в уравнении Ленгмюра аналогичная величина обозначалась aj) с —константа. Значение константы с определяет форму начального участка изотермы. Обратим внимание на то, что, несмотря на схожесть обозначений, в уравнении БЭТ с — не концентрация. Константу с можно рассчитать термодинамически: Если Qадс << QК0НД, то изотерма относится ко II или IV типу, если Оадс > > Окоцд — то к III или V типу. Уравнение БЭТ широко используется для определения удельной поверхности адсорбента. Наиболее распространенным адсорбентом для определения является азот, поскольку он показывает близкие значения константы с для большинства твердых поверхностей. Определение сводится к нахождению предельной адсорбции по опытным данным. Рассчитывают удельную поверхность S^ но уравнению: Где NA— число Авогадро; S0— площадь, занимаемая одной молекулой газа или пара в адсорбционном слое («посадочная площадка»). Предельная адсорбция A∞ по экспериментальным данным должна выражаться числом молей адсорбата на единицу массы адсорбента (моль/кг). Для определения удельной поверхности по методу БЭТ обычно используют инертные газы: азот, аргон или криптон. Такие газы проявляют слабое межмолекулярное взаимодействие на поверхности адсорбента, что находится в соответствии с исходными допущениями теории и обеспечивает достоверность полученных результатов. Для увеличения адсорбции таких газов опыт проводится при низких температурах (отсюда еще одно название — метод низкотемпературной адсорбции). УравнениеБЭТ применяется с хорошим приближением в области давлений При меньших соотношениях в результаты вносит искажение неоднородность поверхности, при больших — сказывается взаимодействие между адсорбированными молекулами. Следует отметить, что в результате измерений по БЭТ можно получить изотерму только кажущейся адсорбции. Основной недостаток метода БЭТ состоит в том, что образец изучается в сухом состоянии, которое может существенно отличаться от влажного состояния адсорбента, контактирующего с исследуемым раствором. Вследствие этого при высушивании осажденных адсорбентов их удельная поверхность может значительно снижаться. Особенно сложно определять удельную поверхность гранулированных твердых веществ — либо из-за неполного их смачивания при используемых условиях, либо из-за диспергирования субстрата при получении свежей поверхности. Ряд материалов, например, глины, тальк и целлюлоза, могут набухать при контакте с полярными жидкостями и применение азота в качестве адсорбата для них становится сомнительным. Возможным способом определения площади «влажной» поверхности является изучение адсорбции из раствора молекул органических веществ, например, бутанола. В лабораторном практикуме удельная поверхность активированного угля находится из соотношения Значение предельной гиббсовской адсорбции находят из экспериментальных данных по зависимости Г=f(c). Для этого измеряют поверхностное натяжение ряда растворов с известной начальной концентрацией. По изотерме поверхностного натяжения определяют значения адсорбции для нескольких концентраций (не менее пяти), строят изотерму адсорбции (предпочтительно в обратных координатах) и находят . Использованная литература 1. А.С. Вячеславов, Е.А. Померанцева, Методическая разработка «Измерение площади поверхности и пористости методом капиллярной конденсации азота», МГУ, Москва 2006, С. 55. 2. О. В. Нецкина, Методическое пособие « Адсорбция из растворов на твердой поверхности», НГУ, Новосибирск 2015, С. 17. 3. А.А.Лопаткин, Теоретические основы физической адсорбции, М. изд. МГУ, 1983.