Еще две замечательные точки.
реклама

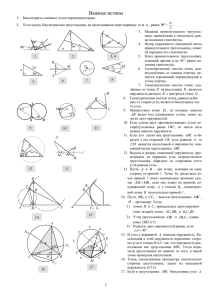
Еще две замечательные точки. 1. Вспомните все известные Вам замечательные точки треугольника. Сделайте соответствующие чертежи. 2. Перечислите теоремы, которые доказываются с помощью «замечательных» точек. I этап. Рассмотрите центры вневписанных окружностей. Исследуйте:1) их положение; 2) взаимосвязь периметра треугольника отрезков касательных; Задача1. В треугольнике ВАС проведены биссектрисы ВL и АК. Отрезок КL лежит на биссектрисе угла АКС . Найдите угол А. Задача 2. С помощью вневписанной окружности доказать, что S = R∙pH, где S – площадь остроугольного треугольника АВС, R – радиус описанной окружности, pHполупериметр ортоцентрического треугольника Н1Н2Н3. Задача 3. Доказать, что точка касания вневписанной в треугольник окружности со стороной, инцентр и середина высоты, проведенной к этой же стороне, лежат на одной прямой. II этап. Рассмотрим точку пересечения биссектрисы внутреннего угла треугольника с окружностью, описанной около этого треугольника; это три аналогичные точки: К1, К2, К3. Доказать теоремы: 1. Через точку Кi проходит серединный перпендикуляр к соответствующей стороне треугольника АВС. 2. Справедлива "теорема трилистника": КсА = КсВ = КсI. Задача 4. Определите вид треугольника АВС, если АКА = ВКВ = СКС. Задача 5. Докажите, что биссектриса АDА угла ВАС делит угол ОАНА пополам. Задача 6. Найдите угол С неравнобедренного треугольника АВС, если центр окружности, описанной около Δ М1М2М3, принадлежит биссектрисе этого угла. (М1, М2, М3 – середины сторон ΔАВС) Задача 7. Для Δ АВС найдите произведение АI∙IКА. Задача 8. Для Δ АВС найдите значение выражения: IK A IK C IB II этап. Рассмотрите точки пересечения биссектрис внутренних углов треугольника и окружности, описанной около этого треугольника.