Важные истины
реклама
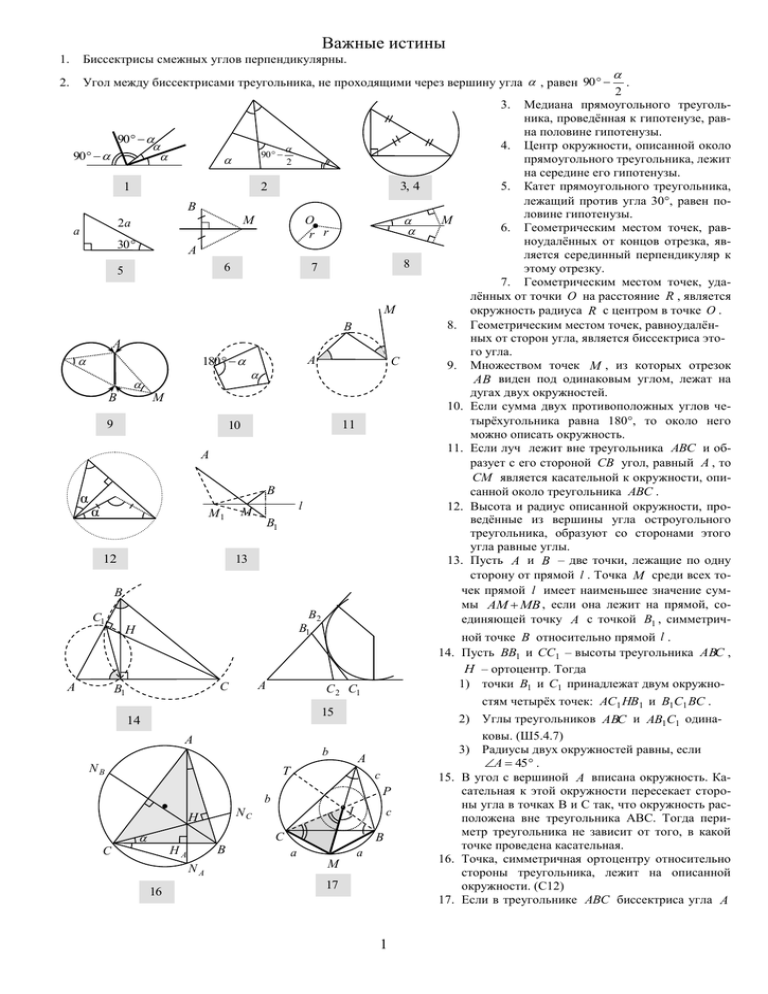
Важные истины 1. Биссектрисы смежных углов перпендикулярны. 2. Угол между биссектрисами треугольника, не проходящими через вершину угла , равен 90 90 90 90 1 2 3, 4 2 В М 2а а 30 О r r 7 8 А 6 5 М В А 180 В А С М 9 11 10 A α B α M1 l M B1 13 12 В С1 А В2 В1 Н А С В1 С 2 С1 15 14 А b NB А Т с Р b С В НА NA 16 с I NC Н С В а М а 17 1 . 2 3. Медиана прямоугольного треугольника, проведённая к гипотенузе, равна половине гипотенузы. 4. Центр окружности, описанной около прямоугольного треугольника, лежит на середине его гипотенузы. 5. Катет прямоугольного треугольника, лежащий против угла 30, равен половине гипотенузы. М 6. Геометрическим местом точек, равноудалённых от концов отрезка, является серединный перпендикуляр к этому отрезку. 7. Геометрическим местом точек, удалённых от точки О на расстояние R , является окружность радиуса R с центром в точке О . 8. Геометрическим местом точек, равноудалённых от сторон угла, является биссектриса этого угла. 9. Множеством точек М , из которых отрезок АВ виден под одинаковым углом, лежат на дугах двух окружностей. 10. Если сумма двух противоположных углов четырёхугольника равна 180, то около него можно описать окружность. 11. Если луч лежит вне треугольника АВС и образует с его стороной СВ угол, равный А , то СМ является касательной к окружности, описанной около треугольника АВС . 12. Высота и радиус описанной окружности, проведённые из вершины угла остроугольного треугольника, образуют со сторонами этого угла равные углы. 13. Пусть А и В – две точки, лежащие по одну сторону от прямой l . Точка M среди всех точек прямой l имеет наименьшее значение суммы AM MB , если она лежит на прямой, соединяющей точку А с точкой B1 , симметричной точке В относительно прямой l . 14. Пусть ВВ1 и СС1 – высоты треугольника АВС , Н – ортоцентр. Тогда 1) точки В1 и С1 принадлежат двум окружностям четырёх точек: АС1 НВ1 и В1С1 ВС . 2) Углы треугольников АВС и АВ1С1 одинаковы. (Ш5.4.7) 3) Радиусы двух окружностей равны, если А 45 . 15. В угол с вершиной А вписана окружность. Касательная к этой окружности пересекает стороны угла в точках В и С так, что окружность расположена вне треугольника АВС. Тогда периметр треугольника не зависит от того, в какой точке проведена касательная. 16. Точка, симметричная ортоцентру относительно стороны треугольника, лежит на описанной окружности. (С12) 17. Если в треугольнике АВС биссектриса угла А пересекает описанную окружность в точке W1 и I – её инцентр, то верна теорема трилистника: CW1 IW1 BW1 . (С12). С1 В А1 18. Высоты остроугольного треугольника АВС являются биссектрисами его ортотреугольника.(С11, Ш5.4.19) b Н а c В1 А d ac bd 19 С 18 β β E B b C b В M γ 19. В четырёхугольник можно вписать окружность тогда и только тогда, когда суммы его противоположных сторон равны. (С10). 20. Описанная окружность делит пополам отрезок между центрами вписанной и вневписанной окружностью. 21. Пусть а и b – основания прямоугольной трапеции, описанной около полукруга радиуса r . Тогда боковые стороны трапеции равны 2r и a b . Окружность с диаметром на большей боковой стороне касается меньшей в её середине 22. 23. 24. 25. 26. 27. Т C γ r M N a I r r А A 20 a D 21 2










