Вариант 9 что 1 миля равна 1,6 км.). B1.

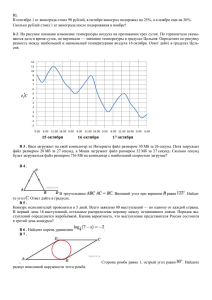
Вариант 9
B1. Спидометр автомобиля показывает скорость в милях в час. Какую скорость (в милях в
час) показывает спидометр, если автомобиль движется со скоростью 48 км в час? (Считайте,
что 1 миля равна 1,6 км.).
B2. Только 92% из 26000 выпускников города правильно решили задачу В2. Сколько человек
правильно решили задачу ?
B3. На рисунке жирными точками показано суточное количество осадков, выпадавших в
Элисте с 7 по 18 декабря 2001 года. По горизонтали указываются числа месяца, по вертикали
— количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности
жирные точки на рисунке соединены линией. Определите по рисунку, сколько дней из
данного периода выпадало менее 2 миллиметров осадков.
B4. Мебельный салон заключает договоры с производителями мебели. В договорах
указывается, какой процент от суммы, вырученной за продажу мебели, поступает в доход
мебельного салона.
Фирмапроизводитель
Процент от выручки, поступающий в
Примечания
доход салона
«Альфа»
5%
Изделия
руб.
«Альфа»
3%
Изделия ценой свыше
руб.
«Бета»
3,5 %
Все изделия
«Омикрон»
4%
Все изделия
ценой
до
В прейскуранте приведены цены на четыре буфета. Определите, продажа какого буфета
наиболее выгодна для салона. В ответ запишите, сколько рублей поступит в доход салона от
продажи этого буфета.
Фирма-производитель Изделие
Цена
«Альфа»
Буфет «Ананий»
14500 руб.
«Альфа»
Буфет «Борислав» 21500 руб.
«Бета»
Буфет «Галактион» 18500 руб.
«Омикрон»
Буфет «Мирослав» 16000 руб.
B5. В треугольнике ABC АВ = ВС. Внешний угол при вершине B равен 126°. Найдите угол C.
Ответ дайте в градусах.
В6. Научная конференция проводится в 4 дня. Всего запланировано 40 докладов — первые
два дня по 9 докладов, остальные распределены поровну между третьим и четвертым днями.
Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М.
окажется запланированным на последний день конференции?
В7. Найдите корень уравнения
корня, укажите меньший из них.
Если уравнение имеет более одного
В8. Дуга окружности
, не содержащая точки , имеет градусную
меру
, а дуга окружности
, не содержащая
точки , имеет градусную меру
.
Найдите вписанный угол
. Ответ дайте в градусах.
В9. На рисунке изображен график
—
производной функции
, определенной на интервале
. Найдите промежутки убывания функции
.
В ответе укажите длину наибольшего из них.
В10. Найдите объем многогранника, вершинами которого являются точки ,
параллелепипеда
, у которого
,
,
.
В11. Найдите значение выражения
,
,
.
В12. Установка для демонстрации адиабатического сжатия представляет собой сосуд с поршнем, резко сжимающим газ. При этом объeм и давление связаны соотношением
,
где (атм.) — давление в газе, — объeм газа в литрах. Изначально объeм газа равен
243,2 л, а его давление равно одной атмосфере. В соответствии с техническими характеристиками поршень насоса выдерживает давление не более 128 атмосфер. Определите, до какого
минимального объeма можно сжать газ. Ответ выразите в литрах.
В13. Найдите объем пирамиды, изображенной на рисунке. Ее основанием является многоугольник, соседние стороны которого перпендикулярны, а одно из боковых ребер перпендикулярно плоскости основания и равно 3.
В14. Улитка ползет от одного дерева до другого. Каждый день она проползает на одно и то же
расстояние больше, чем в предыдущий день. Известно, что за первый и последний дни улитка
проползла в общей сложности 10 метров. Определите, сколько дней улитка потратила на весь
путь, если расстояние между деревьями равно 150 метрам.
В15. Найдите наименьшее значение функции
на отрезке
.
С1.
С2. В правильной четырёхугольной призме ABCDA1 B1 C1 D1 сторона основания равна 11, а
боковое ребро AA1 = 7 . Точка K принадлежит ребру B1 C1 и делит его в отношении 8:3 ,
считая от вершины B1 . Найдите площадь сечения этой призмы плоскостью, проходящей
через точки B, D и K .
С3.
С4. В треугольник ABC вписана окружность радиуса R, касающаяся стороны AC в точке D,
причём AD = R.
а) Докажите, что треугольник ABC прямоугольный.
б) Вписанная окружность касается сторон AB и BC в точках E и F .
Найдите площадь треугольника BEF , если известно, что R = 5 и CD =15.
С5. Найдите все значения a , при каждом из которых уравнение
имеет единственный корень.
С6. Задумано несколько (не обязательно различных) натуральных чисел. Эти числа и все их
возможные суммы (по 2, по 3 и т.д.) выписывают на доске в порядке неубывания. Если какоето число n , выписанное на доске, повторяется несколько раз, то на доске оставляется одно
такое число n ,
а остальные числа, равные n , стираются. Например, если задуманы числа 1, 3, 3, 4, то на доске
будет записан набор 1, 3, 4, 5, 6, 7, 8, 10, 11.
а) Приведите пример задуманных чисел, для которых на доске будет записан набор 3, 6, 9, 12,
15.
б) Существует ли пример таких задуманных чисел, для которых на доске будет записан набор
1, 3, 4, 5, 6, 8, 9, 11, 12, 13, 14, 17, 18, 19, 21, 23?
в) Приведите все примеры задуманных чисел, для которых на доске будет записан набор 8, 9,
10, 17, 18, 19, 20, 27, 28, 29, 30, 37, 38, 39, 47.