Введение «Решение задач – практическое искусство, подобное
реклама

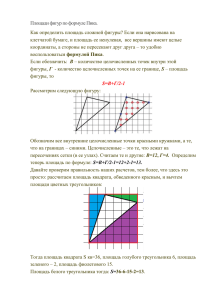
Введение «Решение задач – практическое искусство, подобное плаванию, катанию на лыжах или игре на фортепиано; научиться ему можно, только подражая хорошим образцам и постоянно практикуясь» Д. Пойя Увлечение математикой часто начинается с размышления над какой-то особенно понравившейся задачей. Богатым источником таких задач служат различные олимпиады – школьные, городские, дистанционные, международные. Готовясь к олимпиадам, мы рассмотрели множество разноплановых заданий и выделили группу задач, подход к решению которых нам показался интересным и оригинальным. Это задачи на клетчатой бумаге. У нас возникали вопросы: в чём заключается особенность таких задач, существуют ли специальные методы и приёмы решения задач на клетчатой бумаге. Увидев такие задачи в контрольно – измерительных материалах ОГЭ и ЕГЭ в нашем кабинете математики, решили обязательно исследовать задачи на клетчатой бумаге, связанные с нахождением площади изображённой фигуры. Казалось бы, что увлекательного можно найти на клетчатой плоскости, то есть, на бесконечном листке бумаги, расчерченном на одинаковые квадратики? Оказывается, задачи, связанные с бумагой в клеточку, достаточно разнообразны. Мы научились вычислять площади многоугольников, нарисованных на клетчатом листке. Так и была определена тема для исследования. Объект исследования: задачи на клетчатой бумаге. Предмет исследования: задачина вычисление площади многоугольника на клетчатой бумаге, методы и приёмы их решения. Методы исследования: Теоретические: анализ и синтез. Эмпирические: сравнение. Индуктивный метод – получение выводов из конкретных примеров. Эксперимент. Цель исследования: Проверить формулу Пика для вычисления площадей геометрических фигур в сравнении с формулами геометрии. Гипотеза: Площадь фигуры, вычисленная по формуле Пика равна площади фигуры, вычисленной по формуле планиметрии. А кто же такой Пик? Георг Алекса́ндр Пик (10 августа 1859 — 13 июля 1942) — Пик поступил в университет в Вене в 1875 году. Уже в следующем году он опубликовал свою первую работу по математике, ему было всего лишь семнадцать лет. Он изучал математику и физику, окончил в 1879 г. универститет, получив возможность преподавать оба эти предмета. В 1877 году из Дрезденской Высшей технической школы (Technische Hochschule) переехал Лео Кёнигсбергер, который занял кафедру в венском университете. Он стал руководителем Пика, и 16 апреля 1880 г. Пик защитил докторскую диссертацию “О классе абелевых интегралов” Формула Пика позволит вам с необычайной легкостью находить площадь любого многоугольника на клетчатой бумаге с целочисленными вершинами Формула Пика вычисляется так: А сейчас мы хотели показать вам пример, как с помощью формулы Пика можно найти площадь фигуры на клетчатой решетки. На данном слайде показаны два способа решения задачи на нахождение площади на квадратной решётки. При работе с данной темой, мы рассмотрели доказательство формулы Пика, также доказали справедливость формулы Пика для единичного квадрата. Вывод: Таким образом, рассматривая задачи на нахождение площадей многоугольников, изображенных на клетчатой бумаге, по формулам геометрии и по формуле Пика и сравнивая результаты в таблицах, мы показали справедливость формулы Пика и пришли к выводу, что площадь фигуры, вычисленная по формуле Пика равна площади фигуры, вычисленной по выведенной формуле геометрии. Итак, наша гипотеза оказалась верной.