Площади фигур по формуле Пика.
реклама
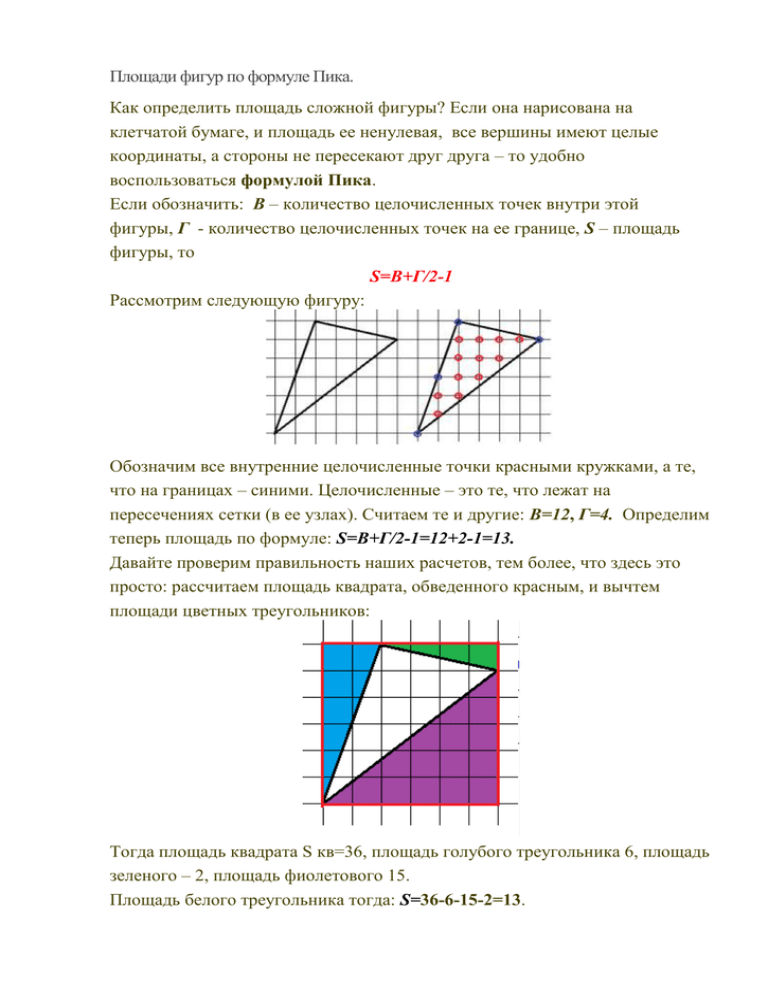
Площади фигур по формуле Пика. Как определить площадь сложной фигуры? Если она нарисована на клетчатой бумаге, и площадь ее ненулевая, все вершины имеют целые координаты, а стороны не пересекают друг друга – то удобно воспользоваться формулой Пика. Если обозначить: В – количество целочисленных точек внутри этой фигуры, Г - количество целочисленных точек на ее границе, S – площадь фигуры, то S=В+Г/2-1 Рассмотрим следующую фигуру: Обозначим все внутренние целочисленные точки красными кружками, а те, что на границах – синими. Целочисленные – это те, что лежат на пересечениях сетки (в ее узлах). Считаем те и другие: В=12, Г=4. Определим теперь площадь по формуле: S=В+Г/2-1=12+2-1=13. Давайте проверим правильность наших расчетов, тем более, что здесь это просто: рассчитаем площадь квадрата, обведенного красным, и вычтем площади цветных треугольников: Тогда площадь квадрата S кв=36, площадь голубого треугольника 6, площадь зеленого – 2, площадь фиолетового 15. Площадь белого треугольника тогда: S=36-6-15-2=13. Рассмотрим такую фигуру: Для нее S=В+Г/2-1=4+3-1=6. Проверим: Тогда площадь прямоугольника Sпр=20, площадь голубого треугольника 5, площадь зеленого – 4, площадь фиолетового 5. Площадь искомой фигуры тогда: S=20-5-4-5=6. Третья фигура: Для нее S=В+Г/2-1=4+4-1=7. Проверим: площадь треугольников, составляющих нашу фигуру: голубого – 4, зеленого – 1, оранжевого – 2. Сумма их площадей S=4+1+2=7. Еще две фигуры: Площадь первой: S=10+2-1=11, второй – S=10+5-1=14. Проверить правильность расчета их площадей вы можете самостоятельно. Теорема Пика. Пусть — число целочисленных точек внутри многоугольника, — количество целочисленных точек на его границе, его площадь. Тогда справедлива формула Пика: Пример. Для многоугольника на рисунке (желтые точки), (синие точки, не забудьте о вершинах!), поэтому квадратных единиц. — Вот здесь вы можете сами строить различные многоугольники, а площадь их будет вычислена по формуле Пика (многоугольники, присутствующие в этой статье, построены именно там). Доказательство теоремы Пика. Сначала заметим, что формула Пика верна для единичного квадрата. Действительно, в этом случае мы имеем и . Рассмотрим прямоугольник со сторонами, лежащими на линиях решетки. Пусть длины его сторон равны и . Имеем в этом случае и, по формуле Пика, Рассмотрим теперь прямоугольный треугольник с катетами, лежащими на осях координат. Такой треугольник получается из прямоугольника со сторонами и , рассмотренного в предыдущем случае, разрезанием его по диагонали. Пусть на диагонали лежат целочисленных точек. Тогда для этого случая и получаем, что Теперь рассмотрим произвольный треугольник. Его можно получить, отрезав от прямоугольника несколько прямоугольных треугольников и, возможно, прямоугольник (см. рисунки). Поскольку и для прямоугольника, и для прямоугольного треугольника формула Пика верна, мы получаем, что она будет справедлива и для произвольного треугольника. Остается сделать последний шаг: перейти от треугольников к многоугольникам. Любой многоугольник можно разбить на треугольники (например, диагоналями). Поэтому нужно просто доказать, что при добавлении любого треугольника к произвольному многоугольнику формула Пика остается верной. Пусть многоугольник и треугольник имеют общую сторону. Предположим, что для формула Пика справедлива, докажем, что она будет верна и для многоугольника, полученного из добавлением . Так как и имеют общую сторону, то все целочисленные точки, лежащие на этой стороне, кроме двух вершин, становятся внутренними точками нового многоугольника. Вершины же будут граничными точками. Обозначим число общих точек через и получим — число внутренних целочисленных точек нового многоугольника, — число граничных точек нового многоугольника. Из этих равенств получаем Так как мы предположили, что теорема верна для то и для по отдельности, Тем самым, формула Пика доказана. К сожалению, эта замечательная формула не обобщается на большие размерности, даже на трехмерный случай. Это показал Рив. Рассмотрим тетраэдр Рива, вершины которого имеют координаты (Здесь — произвольное натуральное число.) При любом внутри этого тетраэдра нет ни одной целочисленной точки, а на границе нет никаких целочисленных точек, кроме и . Таким образом, при различных объемах и площадях поверхностей данных тетраэдров число целочисленных точек, которые лежат внутри них и на их границах, остается неизменным, и обобщения формулы Пика получить не удается. Однако некоторое обобщение получается с помощью полиномов Эрхарта.