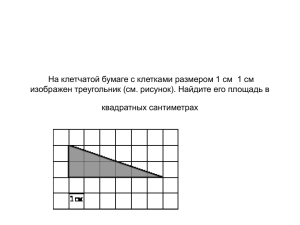
Фестиваль ученических проектов- 2018 Муниципальное Бюджетное Общеобразовательное Учреждение «Средняя общеобразовательная школы п .Керамкомбинат» Секция - Точные науки, предмет- Математика Тип проекта - исследовательский «Задачи на клетчатой бумаге» Выполнила: учащаяся: 9 «А» класса Глушкова Анастасия Руководитель: Терещенко Светлана Васильевна учитель математике первой квалификационной категории 2018 1 Содержание Введение………………………………………………………………2 - 4 Основная часть……………………………………………………….. Глава 1. Решение задач по формулам ………………………............5-8 Глава 2. Задачи из ОГЭ вычислить величины угла, синуса, косинуса, тангенса угла на клетчатой бумаге……………………………………………..9 Глава 3. Нахождение расстояния между точками, от точки до прямой…………………………………………………………………10 Глава 4.Формула Пика………………………………………………..11-13 Игра ………………………………………………………………… . 14 Заключение. ………………………………………………………… 15 Список использованной литературы….…………………………………………….....................16 2 Введение: Увлечение математикой часто начинается с размышления над какой-то особенно понравившейся задачей. Я рассмотрела множество разных заданий и больше всего мне понравились такие как задачи на клетчатой бумаге. Оказывается, задачи, связанные с бумагой в клеточку, достаточно разнообразны. Есть задачи на нахождение: 1) Площади фигуры или ее части на клетчатой бумаге; 2) Величины угла, синуса, косинуса, тангенса угла. 3) Задачи на доказательство и т.д. Мы рассмотрели четыре способа решения таких задач: 1.Метод непосредственных вычислений 2.Метод дополнения 3.Метод разделения 4.С помощью формулы Пика 1.Основной вопрос проекта: Задачи на клетчатой бумаге? Объект исследования: Задачи разного вида. Предмет исследования: Задачи по математике на клетчатой бумаге. Цель: Рассмотреть задачи на клетчатой бумаге. 2.Задачи: 1.Изучить историю вопроса. 2.Познакомить с формулой Пика и показать ее применение при решении задач. 3.Узнать больше о задачах по математике на клетчатой бумаге и показать решение их. 4.Сделадь вывод. 5.Сделать слайдовую презентацию на тему: «Математика на клетчатой бумаге ». 3.Методы исследования: 3 Сбор материала, обработка данных, наблюдение ,сравнение ,анализ. 4.План работы по организации проекта 1. Подготовительно – организационный ( 1 четверть ) 2. Самостоятельная творческая деятельность ( сентябрь – январь ) 3. Реализация проекта ( второе полугодие учебного года - февраль месяц, с 10 – 14 февраля ) 4.Деятельность по реализации проекта НА первом этапе составили план работы. Нашли и изучили дополнительную литературу. Рассмотрели задачи, входящие в базу данных по ОГЭ. Второй этап выполнения проекта . После того ,как мы самостоятельно изучили всю необходимую литературу, составили план проекта, исследовали и сформулировали цели и задачи проекта , мы стали работать над проектом. Третий этап реализация проекта. Оформили проектную работу и выступили перед классом. 4 Основная часть. Глава 1. Решение задач по формулам . Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в квадратных сантиметрах. 2.Задание B3 (№ 251249) Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). Ответ дайте в квадратных сантиметрах. 3.Задание B3 (№ 5193) Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). Ответ дайте в квадратных сантиметрах. 4.Задание B3 (№ 249883) Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). Ответ дайте в квадратных сантиметрах. 5 5.Задание B3 (№ 248775) Найдите площадь квадрата, изображенного на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). Ответ дайте в квадратных сантиметрах. 6.Задание B3 (№ 5187) Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в квадратных сантиметрах. 7.Задание B3 (№ 246707) Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). Ответ дайте в квадратных сантиметрах. 6 8.Задание B3 (№ 257919) Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). Ответ дайте в квадратных сантиметрах. Задача № 9. . На клетчатой бумаге с размером клетки 1x1 изображена фигура. Найдите её площадь. 1.Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 7 На клетчатой бумаге с размером клетки 1x1 изображён треугольник ABC. Найдите длину его высоты, опущенной на сторону AС 37. 1 см × 1 см. Ответ дайте в квадратных сантиметрах. Есть формула расчета площади треугольника: S= снование*высота/2 S=4*8/2= 16 Ответ: 16 9.Задание B3 (№ 263465) Найдите (в см2) площадь фигуры, изображенной на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). В ответе запишите 10..Найдите (в см2) площадь бумаге с размером клетки 1 см . фигуры, изображенной на клетчатой 1 см (см. рис.). В ответе запишите 8 . Глава2. Задачи из ОГЭ вычислить величины угла, синуса, косинуса, тангенса угла на клетчатой бумаге. . Найдите тангенс угла AOB, изображенного на рисунке. 2. Найдите тангенс угла А треугольника ABC, изображённого на рисунке. 3. Найдите тангенс угла B треугольника ABC, изображённого на рисунке. 4. Найдите тангенс угла С треугольника ABC , изображённого на рисунке. 9 Глава 3. Нахождение расстояния между точками, от точки до прямой; . На клетчатой бумаге с размером клетки 1 см × 1 см отмечены точки А, В и С. Найдите расстояние от точки А до середины отрезка ВС. Ответ выразите в сантиметрах. 26. На клетчатой бумаге с размером клетки 1 см × 1 см отмечены точки А, В и С. Найдите расстояние от точки А до середины отрезка ВС. Ответ выразите в сантиметрах. 10 Глава 4. Формула Пика Георг Пик – австрийский математики. Он известен своей теоремой о вычислении площади многоугольника, которая появилась в его восьмистраничной работе 1899 года. Эта теорема оставалась незамеченной в течение некоторого времени после того, как Пик её опубликовал, однако в 1949 г. польский математик Гуго Штейнгауз включил теорему (или как её ещё называют — формулу) в свой знаменитый «Математический калейдоскоп». С этого времени теорема Пика стала широко известна. В Германии формула Пика включена в школьные учебники [1, с. 2]. Оказывается, площади многоугольников, вершины которых расположены в узлах сетки, можно вычислять гораздо проще: есть формула, связывающая их площадь с количеством узлов, лежащих внутри и на границе многоугольника. Эта замечательная и простая формула называется формулой Пика [2 с. 2]. Линии, идущие по сторонам клеток, образуют сетку, а вершины клеток – узлы этой сетки. Нарисуем на листе многоугольник с вершинами в узлах (Приложение 1, рис. 1) и найдем его площадь. Искать её можно по-разному. Например, можно разрезать многоугольник на достаточно простые фигуры, найти их площадь и сложить. Но тут нас ждёт много хлопот. Решение приведено в практической части работы в п. 2.1. Но можно найти площадь этого же многоугольника, используя формулу Пика: где S – площадь фигуры; В - количество вершин клеток внутри фигуры; Г - количество пересечений контура фигуры с вершинами клеток. Эта формула верна как для прямоугольников, так и для произвольных многоугольников с вершинами в узлах сетки. Обозначим все внутренние целочисленные точки красными кружками, а те, что на границах – синими. Целочисленные – это те, что лежат на пересечениях сетки (в ее узлах). Считаем те и другие: В=12, Г=4. Определим теперь площадь по формуле: S=В+Г/2-1=12+2-1=13. 11 Для нее S=В+Г/2-1=4+3-1=6. Проверим: Тогда площадь прямоугольника Sпр=20, площадь голубого треугольника 5, площадь зеленого – 4, площадь фиолетового 5. Площадь искомой фигуры тогда: S=20-5-4-5=6. Третья фигура: второй – S=10+5-1=14. Проверить правильность расчета их площадей вы можете самостоятельно. 12 13 Игра на клетчатой бумаге 1) Крестики – нолики Популярная игра в крестики – нолики состоит в следующем. Двое по очереди рисуют на листе клетчатой бумаги крестики и нолики. Первый игрок рисует крестики, второй – нолики. Выигрывает тот, кто первым поставит определённое количество своих знаков в ряд (по вертикали, горизонтали или диагонали). Следующая задача относится к этой игре. относится к этой игре. 14 Заключение Головоломки увлекают решением задач на клетчатой бумаге, прежде всего потому, что универсального метода решения таких задач не существует, и каждый, кто берётся за их решение, может в полной мере проявить свою смекалку. Задачи на клетчатой плоскости являются серьёзными и полезными. Основной метод, который использовался в проекте - это метод систематизации и обработки данных. При всем многообразии задач на клетчатой бумаге чёткой классификации и структурирования по методам и способам решения я не встретила. Очень вероятно, потому, что для многих задач на бумаге в клетку нет общего правила решения, конкретных способов и приёмов. Вот это их свойство обуславливает их ценность для развития не конкретного учебного умения или навыка, а вообще умения думать, размышлять, анализировать, искать аналогии, то есть, эти задачи развивают мыслительные навыки. При выполнении проекта я расширила свои знания о решении задач на клетчатой бумаге, определила для себя классификацию исследуемых задач, убедилась в их многообразии. Я научилась вычислять площади многоугольников, нарисованных на клетчатом листке, познакомилась с совсем новыми, необычными «расстояниями», узнала, как раскраска клеточек помогает решать многие задачи, а также познакомилась поближе с задачами на разрезание и, наконец, научилась играть в увлекательные игры на листке бумаги в клетку. «Математика в клетку» является занимательным элементом обычной математики и считается альтернативным, а во многом и незаменимым способом решения многих задач. 15 Литература: 1.Жарковская Н. М., Рисс Е. А . Геометрия клетчатой бумаги. Формула Пика // Математика, 2009, № 17, с. 24-25. 2.Задачи открытого банка заданий по математике ФИПИ. 3.Смирнова И. М., Смирнов В. А . Геометрия на клетчатой бумаге. – М.: Чистые пруды, 2009. 4.Смирнова И. М., Смирнов В. А . Геометрические задачи с практическим содержанием. – М.: Чистые пруды, 2010. 16