Построение параболы по методу наименьших квадратов Чтобы понять, как одна величина
реклама

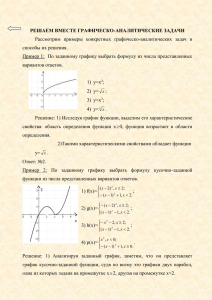
Построение параболы по методу наименьших квадратов Чтобы понять, как одна величина y зависит от другой величины x , например длина стержня y от температуры x показатель преломления y данного материала от длины световой волны x высота свободно падающего тела y от времени x , мы проводим ряд экспериментов и получаем следующую таблицу. X1 X2 … Xi … Xn Y1 Y2 … Yi … Yn Для наглядного представления этих данных их следует изобразить на координатной плоскости, нанеся на нее n точек с координатами ( X i , Yi ) . Может оказаться, что полученные точки расположены вдоль некоторой параболы, и мы можем предположить, что зависимость между величинами x и y квадратичная. И только ошибки измерений вызывают некоторые небольшие отклонения полученных экспериментальных точек от некоторой параболы. Возникает задача нахождения параболы, которая лучше всего описывает эти экспериментальные данные. Запишем уравнение параболы в виде (1) y ( x ) a0 a1 x a2 x 2 . И тогда задача нахождения наилучшей параболы сводится к задаче нахождения ее коэффициентов a0 , a1 , a3 . Какую же параболу следует считать наилучшей? Чтобы ответить на этот вопрос, для каждой точки ( X i , Yi ) вычислим отклонение по вертикали от параболы, заданной уравнением (1), до этой точки i Yi y ( X i ) . Эти расстояния, измеренные по вертикали, называются невязками. Для параболы, наилучшим образом описывающей наши данные, каждая из этих невязок должна быть мала – они должны быть малы в совокупности. В качестве критерия малости невязок выбирается сумма их квадратов S (a0 , a1 , a2 ) i (Yi y( X i )) 2 (Yi (a0 a1 X i a2 X i )) 2 . 2 2 Чем меньше эта сумма, тем лучше парабола y ( x ) a0 a1 x a2 x 2 описывает наши данные. Таким образом, наилучшая парабола – это та, для которой сумма S (a1 , a2 , a3 ) минимальна. Минимум суммы S (a1 , a2 , a3 ) ищем, приравнивая ее частные производные нулю S 2 a 2 (Yi ( a0 a1 X i a2 X i )) 0 0 S 2 2 (Yi ( a0 a1 X i a2 X i )) X i 0 . a1 S 2 2 2 (Yi ( a0 a1 X i a2 X i )) X i 0 a2 Или na0 a1 X i a2 X i 2 Yi 2 3 a0 X i a1 X i a2 X i X iYi . 2 3 4 2 a0 X i a1 X i a2 X i X i Yi Это система из трех уравнений с тремя неизвестными a0 , a1 , a3 , после решения которой получаем параболу y ( x ) a0 a1 x a2 x 2 , наилучшим образом описывающую наши данные по методу наименьших квадратов. Аналогичным образом может быть построен кубический многочлен y ( x ) a0 a1 x a2 x 2 a3 x 3 , наилучшим образом описывающую наши данные по методу наименьших квадратов. Его коэффициенты являются решением следующей системы из четырех уравнений с четырьмя неизвестными na0 a1 X i a2 X i 2 a3 X i 3 Yi 2 3 4 a0 X i a1 X i a2 X i a3 X i X iYi . 2 3 4 5 2 a X a X a X a X X Y 0 i i i 1 i 2 i 3 i 3 4 5 6 3 a0 X i a1 X i a2 X i a3 X i X i Yi В Mathcad имеются собственные средства, реализующие метод наименьших квадратов – это функции regress и interp.