Москва 2006 Содержание. - Институт прикладной математики

ОРДЕНА ЛЕНИНА
ИНСТИТУТ ПРИКЛАДНОЙ МАТЕМАТИКИ
имени М.В.Келдыша
РОССИЙСКОЙ АКАДЕМИИ НАУК
И.С. Барская, С.И. Мухин, В.М. Чечеткин
Математическое моделирование
равновесных конфигураций
самогравитирующего газа.
Москва
2006
3
Содержание.
1. Введение. ........................................................................................................................ 3
2. Модель равновесной конфигурации самогравитирующего газового облака. ......... 4
3. Вычислительный алгоритм. .......................................................................................... 6
4. Расчеты эволюции системы при разных скоростях вращения и различных
граничных условиях для гравитационного потенциала. ............................................. 10
5. Заключение. .................................................................................................................. 14
6. Список литературы. ..................................................................................................... 15
1. Введение.
Одной из актуальных, недостаточно изученных и требующих дальнейшего
исследования проблем математического моделирования эволюции звезд является
построение равновесных конфигураций гравитирующих газовых тел [1-6]. Такие
конфигурации важны для моделирования газодинамических процессов на этапах
образования нейтронных звезд или черных дыр, а также для моделирования
коллапса и вспышек сверхновых.
В настоящей работе звезда рассматривается как самогравитирующее газовое
облаком и решается задача построения ее равновесных конфигураций, как с
учетом вращения так и без него.
В отсутствии вращения звезда имеет сферическую форму, поверхности
постоянного давления – изобарические поверхности – являются концентрическими
сферами, и все газодинамические параметры обладают центральной симметрией
[7]. В этом случае равновесные конфигурации можно построить аналитически и
определить газодинамические параметры в явном виде. Такие конфигурации
использовались в предлагаемой в работе в качестве тестовых.
Если газ вращается вокруг фиксированной в пространстве оси с некоторой
заданной угловой скоростью, то, как показано в работе [1], форма звезды
становится эллипсовидной. В этом случае равновесные конфигурации звезды
можно построить аналитически только при специальных ограничениях на
газодинамические параметры, а в общем случае задачу приходится решать
численно [1].
Одной из основных функций, определяющих изучаемую нами равновесную
конфигурацию самогравитирующего тела, является гравитационный потенциал.
Гравитационное поле вне тела со сферически симметричным распределением
вещества зависит только от полной массы притягивающего тела. Распределение
гравитационного потенциала внутри звезды описывается уравнением Пуассона [7],
основной трудностью при решении этого уравнения является выбор граничных
условий [2, 8, 11]. В данной работе для численного моделирования
самогравитирующей вращающейся звезды и получения ее равновесных
конфигураций используются три различных типа граничных условий для
уравнения Пуассона и проводится сравнение полученных решений.
Работа выполнена при поддержке РФФИ, грант 03-01-00311.
4
2. Модель равновесной конфигурации самогравитирующего газового облака.
Как показывают наблюдения [1], большая часть звезд находится в состоянии
гидростатического равновесия, и поэтому значительный интерес с точки зрения
астрофизики представляют собой различные стационарные и квазистационарные
образования вращающегося самогравитирующего газа. Особенно важно
исследовать процессы, которые приводят начальную конфигурацию газового
облака к таким стационарным состояниям. В рамках предлагаемой модели
равновесные конфигурации можно получить за счет равновесия силы
собственного тяготения, центробежной силы и градиента газового давления,
решив систему трехмерных уравнений газовой динамики [8]:
 (r )  (r u ) 1  (r v)  (r w)



0,
t
r
r 
z
 (r u )  (r u 2  r p) 1  (r u v)  (r u w)



 p   v 2  r Fr ,
t
r
r 
z
 (r v)  (r v u) 1  (r v 2  r p)  (r v w)



   u v  r F ,
t
r
r

z
(2.1)
 (r w)  (r w u ) 1  (r w v)  (r w2  r p)



 r Fz ,
t
r
r

z
 (r e)  (r u h) 1  (r v h)  (r w h)



 r ( F , v ) ,
t
r
r 
z
e    u 2 2  v 2 2  w2 2 , h  e  p  .
Уравнения (2.1) записаны в цилиндрической системе координаты r,, z  . Для
замыкания системы (2.1) используем уравнение состояния идеального газа:
p  (  1)   .
(2.2)
Здесь r - радиус,  - полярный угол, t - время,  - плотность газа, p - давление,
 - удельная внутренняя энергия, e - полная удельная энергия,  - показатель
адиабаты, h - полная удельная энтальпия, v  (u, v, w)T - скорость газа, u - ее
радиальная компонента, v - азимутальная, w - компонента скорости по оси z, F суммарная удельная сила с компонентами (Fr , F , Fz ) , действующая на частицу
газа. Сила F в данной задаче – это сила гравитации, которая выражается через
гравитационный потенциал Ф:
F   grad () ,
а гравитационный потенциал удовлетворяет уравнению Пуассона:
   4 G ,
(2.3)
5
где G – гравитационная постоянная [7].
Будем решать задачу в безразмерном виде. В качестве масштабных величин
выберем {  0,l0 ,t0 }, где l0 - характерный пространственный размер задачи,  0 плотность в центре звезды, t0 - характерный временной масштаб. В безразмерных
переменных, выбранных согласованным образом, система уравнений (2.1),
уравнение (2.2) и (2.3) сохраняют прежний вид.
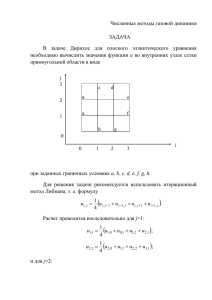
Систему уравнений (2.1), (2.2), (2.3) в силу симметрии относительно
плоскости z = 0 будем решать в области  (Рис.1):
  (0  r  r2 )  (0    2 )  (0  z  z2 ) .
(2.4)
На «внешней» границе этой цилиндрической области (r = r2 , z = z2) в
качестве граничных условий поставим «свободные» условия:
f
r
 0,
r  r2
f
z
0
,
(2.5)
zz2
где f – это одна из функций ρ, p, u, v, w, h. На «нижней» (z = 0) и «внутренней»
(r = 0) границе - условия симметрии.
Поскольку мы ищем стационарные конфигурации, на данном этапе работы
будем полагать, что сила гравитации обладает осевой симметрией, что позволит
ограничиться
рассмотрением двумерного уравнения Пуассона для
гравитационного потенциала. При этом расчет газодинамических параметров
будем проводить в трехмерном случае, что позволит нам исследовать
устойчивость осесимметричных газодинамических состояний.
Исключим из уравнения (2.3) слагаемые связанные с производной по углу φ,
и будем его решать в двумерной области G   0  r  r2 ,0  z  z2  . Область G - это
подобласть области Ω при фиксированном угле φ. Обозначим символом Г
прямоугольную границу области G, которая состоит из четырех отрезков: Г1 –
левая сторона прямоугольника, Г2 – верхняя сторона прямоугольника, Г3 – правая
сторона прямоугольника и Г4 – нижняя сторона прямоугольника (Рис.1).
В области G задача для гравитационного потенциала примет вид:
 1      2 
 r r  r r   z 2  4 G ( r, z, t ) , ( r, z )  G





   0 ,
0,
 Г , Г   ( r, z, t )
2
3
 r Г1
z Г 4
.
(2.6)
В качестве краевых условий для этой задачи на границе Г2 и Г3 возьмем
функцию  (r , z , t ) , представляющую собой точное значение гравитационного
потенциала:
 (r , z, t )  G 
G
 (r , z , t )
(r  r ) 2  ( z  z ) 2
dG .
6
Система (2.1), (2.2), (2.6) решается совместно, так как для нахождения силы
гравитации, компоненты которой входят в правую часть системы уравнений
газовой динамики (2.1) используется функция плотности.
В качестве начальных данных для системы уравнений (2.1), (2.2), (2.6)
возьмем гидростатически равновесную стационарную конфигурацию, которую,
можно найти [7], задав распределение плотности, из системы уравнений:
GM ( r ) 
 dp
 dr  
r2
 dM

 4 r 2 
 dr
 p  p(  ,  )

.
(2.7)
3. Вычислительный алгоритм.
Систему уравнений (2.1), (2.2), (2.6) будем решать численно, разбиением по
процессам: газодинамическому и гравитационному. В начальный момент времени
найдем распределение всех газодинамических параметров, решив систему
уравнений (2.7). Затем, зная распределение плотности, найдем распределение
гравитационного потенциала, численно решив задачу (2.6). Это распределение
потенциала используем для нахождения силы гравитации, стоящей в правой части
системы уравнений (2.1), и, наконец, численно решив систему (2.1), найдем
распределение физических параметров в следующий момент времени.
Запишем систему уравнений газовой динамики (2.1) в цилиндрической
системе координат в виде:
q F 1 G H



  , где
t r r  z
(3.1)
q   r , r u, r v, r w, r e
(3.2)
T
F   r u, r u 2  rp, r uv, r u w, r uh
T
G   r v, r uv, r v 2  rp , r v w, r vh
T
H   r w, r u w, r v w, r w2  rp, r wh
T


 
  0, p   v 2  r Fr ,   vu  r F , r Fz , r ( F , v )
T
Для решения этой системы уравнений в области  построим сетку
  r     z , где

 r  ri ; ri  r1  i  r ; i  0,..., N r  1 ; r 

r2 

Nr 
7


   i ;  i  i   ; i  0,..., N   1 ;  

 z   z i ; z i  i  z ; i  0,..., N z  1 ; z 

2 

N  
(3.3)
z2 

Nz 
Будем использовать явную разностную схему первого порядка
аппроксимации - схему Роу, которая в цилиндрической системе координат
представляется в виде [14]:
qˆi , j ,k  qi , j ,k


Fi 1/ 2, j ,k  Fi 1/ 2, j ,k
r

Gi , j 1/ 2,k  Gi , j 1/ 2,k
r

H i , j ,k 1/ 2  H i , j ,k 1/ 2
z
 i , j ,k ,
где qˆi , j ,k  q( ri ,  j , zk , tn1 ) - функции с верхнего временного слоя, а потоки в
полуцелых точках вычисляются по следующим формулам:
A
F
G
H
,B 
,C 
,
q
q
q
v  u, v, w ,
T
v2
P v2
e    ,h     ,
2
 2
0
0
2
1 
 1
 uc
0
0
2u u  c 

RA   v
2c
0
2v
v ,


0
2c 2 w
w 
 w
 h  uc 2vc 2 wc v 2 h  uc 


 A  diagu  c, u, u, u, u  c,
Fi 1/ 2, j ,k 
Fi , j ,k  Fi 1, j ,k
2

1
 Am (qi*1/ 2, j,k ) sim1/ 2, j,k rAm (qi*1/ 2, j,k ),
2 m
8
si1,5
1/ 2, j ,k 
si21/ 2, j ,k 
si31/ 2, j ,k 
si41/ 2, j ,k 
1
*2
i 1/ 2, j ,k
2c
1
*2
i 1/ 2, j ,k
2c
1
2
*
i 1/ 2, j ,k
2c
1
( Pi 1, j ,k  Pi , j ,k ) i*1/ 2, j ,k ci*1/ 2, j ,k (ui 1, j ,k  ui , j ,k )  ,
 i*1/ 2, j ,k ci*1/ 2, j ,k (vi 1, j ,k  vi , j ,k )  ,
 i*1/ 2, j ,k ci*1/ 2, j ,k ( wi 1, j ,k  wi , j ,k )  ,
 ci*1/ 2, j ,k ( i 1, j ,k  i , j ,k )  ( Pi 1, j ,k  Pi , j ,k )  ,


2
*2
i 1/ 2, j ,k
2c
i*1/ 2, j ,k  i 1, j ,k i , j ,k ,
vi*1/ 2, j ,k 
hi*1/ 2, j ,k 
*
i 1/ 2, j ,k
c

i , j ,k vi , j ,k  i 1, j ,k vi 1, j ,k
i , j ,k  i 1, j ,k
i , j ,k hi , j ,k  i 1, j ,k hi 1, j ,k
i , j ,k  i 1, j ,k
,
,
i , j ,k ci2, j ,k  i 1, j ,k ci21, j ,k
i , j ,k  i 1, j ,k

 1
i 1, j ,k i , j ,k
2 ( i , j ,k  i 1, j ,k )
2
(vi 1, j ,k  vi , j ,k )2 .
Аналогично записываются выражения для Gi , j 1/ 2,k и для H i , j ,k 1/ 2 .
Компоненты силы гравитации (Fr , F , Fz ) , входящие в правую часть  на
каждом временном слое находятся численным решением системы уравнений для
гравитационного потенциала (2.6).
Для решения системы (2.6) аппроксимируем уравнение Пуассона и граничные
условия следующим образом [9]:
1 1 
1
1
r 1
i 1, j  i, j  r 1
i, j  i 1, j
i  , j r
ri, j r  i  , j r
2
 2




1
 i, j1  2 i, j   i, j1   4
z 2
i  1,.. N r ,









G i , j ,
j  1,.. N z
1
i 1, j  i , j  0 , i  0, j  1,.. N z
r
1
 i, j 1   i , j  0 , j  0, i  1,.. N r
z
Правая часть в уравнении (3.4) берется с нижнего временного слоя.
(3.4)
9
В результате такой аппроксимации и после перенумерования переменных
получим систему линейных алгебраических уравнений диагонального вида:
Аy = f ,
(3.5)
матрица которой имеет вид:
a m ,n
 2i 2
  2 , при m  k * N 1  i, n  m, k  1,..., N 2  1 , i  2,..., N 1
 h1 h2
 2
1
2
 2 , при m  k * N 1  1, n  m, k  1,..., N 2  1
 
 h1 2h1 h2
 2
1
2 h
 2  12 , при n  m  1
 
 h1 2h1 h2 h2
 1
i 

  2 , при m  k * N 1  i, n  m  1, k  0,..., N 2  1 , i  1,..., N 1  1
 h1
 1
i 
 2 , при m  k * N 1  i, n  m  1, k  0,..., N 2  1 , i  2,..., N 1
 h1
 ih
 1 , при m  k * N 1  i, n  m  N 1 , k  0,..., N 2  2 , i  1,..., N 1
 h22

 ih1 , при m  k * N  i, n  m  N , k  1,..., N  1 , i  1,..., N
1
1
2
1
 h22
Таким образом, вышеописанная аппроксимация уравнения (2.6) приводит к
необходимости решать систему линейных алгебраических уравнений с
разреженной матрицей. Для этого воспользуемся предложенным в работе [13]
эффективным итерационным методом обращения матрицы А, основанном на
методе сопряженных градиентов с модификацией в виде неполного разложения
Холецкого.
Следуя [13], в целях экономии памяти, будем хранить матрицу А системы
(3.5) в (A0, IA, JA) формате. При использовании этого формата достаточно
”помнить” лишь два массива A0 и JA длиной NА, равной числу ненулевых
элементов матрицы А, и один массив IA длиной N + 1. В одномерном массиве A0
содержатся значения всех ненулевых элементов матрицы А, перебираемые по
строкам, в массиве JA содержатся соответствующие номера столбцов этих
элементов, а каждый элемент IA(i) массива IA указывает номер элемента в массиве
A0, с которого начинается i-ая строка матрицы А.
10
4. Расчеты эволюции системы при разных скоростях вращения и различных
граничных условиях для гравитационного потенциала.
В рамках описанной выше модели решим задачу о равновесии
невращающегося газового шара радиуса l, внутри которого вещество распределено
по следующему закону:

1

 ( R )  1  l R , 0  R  l ,

0
(4.1)
, lR
где R  r 2  z 2 - расстояние от точки, в которой ищется решение, до начала
координат. Как уже было сказано выше, модель обладает осевой симметрией,
поэтому функции, описывающие физические параметры, не зависят от угла φ.
Учитывая, что масса М |R = 0 = 0, и давление p|R ≥ l = 0 , из системы (2.7)
можно найти распределение давления по радиусу R внутри звезды:
p( R )  
 G R2
36l
2
9l
2
 28Rl  24l 2  
5
 Gl 2 , 0  R  l
36
(4.2)
Из уравнения (2.6) найдем распределение гравитационного потенциала:
 2 2 1 3 2
2
 G 3 R  3l R   3  GR

 
( R)  
3
 G l
 3R
положив функцию μ равной 
,Rl
,
(4.3)
,Rl
GM
, что соответствует известному [7] значению
R
гравитационного потенциала в точке, находящейся за пределами гравитирующего
шара массы М и отстоящей на расстоянии R от центра гравитации.
Найденное распределение физических параметров используем в качестве
начальных данных для численного решения системы уравнений (2.1) в области 
и уравнения (2.6) в области G со свободными граничными условиями (2.5) на
внешней границе, условиями симметрии на нижней и внутренней границе и
следующими граничными условиями для гравитационного потенциала:

0,
r r  0

 0 ,  r r , z  z  ( x ) .
2
2
z z  0
(4.4)
Здесь x   (r, , z) эйлеровы пространственные цилиндрические
координаты.
Будем рассматривать три различных типа граничных условий для
гравитационного потенциала на внешней границе.
В первом случае возьмем функцию  ( x ) равной значению гравитационного
потенциала на внешней границе в начальный момент времени (4.3):
11
GM 0
 GL3
 ( x )   (r ,  , z )  (r ,  , z )  ( Rr , , z )  

Rr , , z
3Rr , , z
(4.5)
В каждой точке границы это значение постоянно, то есть не изменяется с
течением времени, здесь Rr , , z – это расстояние до граничной точки с
координатами ( r,  , z ) .
Во втором случае в граничных условиях для потенциала учтем, что масса
звезды изменяется с течением времени. Тогда
( x )  ( x, t)  
GM (t )
Rr , ,z
,
(4.6)
где M (t )    ( x , t ) d  .

В третьем случае для нахождения гравитационного потенциала в граничных
точках используем его точное интегральное представление:
 ( x )  G 

 ( x )
x  x
d ,
(4.7)
аппроксимировав интергал (4.7) в граничных точках Г2 и Г3 по формуле:
 m l n  G 
im
j
k n
M i jk
ml n
Rijk
 G 
im
j
k n
 i j k ri r  z
ri 2  rm2  2ri rm cos( j   l )  ( z j  z n ) 2
(4.8)
В этой формуле Rijkml n - это расстояние от ячейки сетки с координатами i, j, k и
массой M i j k , которая создает потенциал, до ячейки с координатами m, l, n, в
которой ищем потенциал.
Для каждого из трех типов граничных условий проведем серию расчетов по
описанному в пункте 3 алгоритму. Область  (2.4) имеет размеры: r2  z2  1.5l , l =
2 – радиус звезды. Во всех расчетах число ячеек сетки  (3.3) N  50 , а
N r  N z  N , где N варьировалось от 50 до 100. В начальный момент времени
область считалась заполненной покоящимся газом, плотность и давление внутри
звезды распределены в соответствии с формулами (4.1), (4.2).
На рис.2 изображены линии уровня плотности, соответствующие начальному
распределению плотности (4.1), в сечении φ = π/4. На рис.3–8 представлены
характерные картины течения, возникающего в случае использования граничных
условий различного типа, характеризующие распределение плотности в различные
моменты времени. Для каждого типа граничных условий численное решение
представлено на два момента времени. В процессе расчета, исходя из критерия
Куранта, шаг по времени определяется автоматически по формуле:
12


   min r / im ,
i ,m
(4.9)
где 0    1 - параметр схемы, в связи с чем картины течения при различных
граничных условиях сравниваются на ближайшие моменты времени. В таблице 1
показано, какой рисунок соответствует каждому граничному условию, и указаны
соответствующие моменты времени; кроме того, там показано, на каком
временном слое достигается данный момент времени.
Номер
рисунка
Граничные
условия для 
Момент
времени
Номер слоя
по времени
3
4
5
6
7
8
Первого типа
Первого типа
Второго типа
Второго типа
Третьего типа
Третьего типа
7.021
21.75
6.9
21.99
6.976
21.955
400
1180
390
1170
324
1080
Таблица 1.
Из таблицы 1 видно, что использование граничных условий третьего типа для
гравитационного потенциала позволяет достигнуть нужной точности за меньшее
число итераций.
Сравнивая рис.4, 6 и 8, на которых изображены линии уровня плотности на
последний момент времени в сечении φ = π/4, можно заметить, что при
использовании в расчетах граничных условий для гравитационного потенциала
первого и второго типа линии уровня плотности становятся немонотонными, в то
время как использование граничных условий третьего типа к немонотонности не
приводит.
Рассмотрим, как изменяются физические параметры системы. На рис.10
отображены характерные графики изменения массы звезды с течением времени в
случае использования граничных условий первого, второго и третьего типа для
гравитационного потенциала. Из этих графиков видно, что в системе происходит
небольшой отток вещества. Потеря массы составляет примерно 6.3%, 5.8% и 2.1%
в первом, втором и третьем случае соответственно. На рис.9 изображен график
изменения плотности по одному из радиусов на два момента времени (начальный
момент времени t0 = 0 и конечный момент времени (см. таблицу 1)) в случае
использования граничных условий первого, второго и третьего типа. Сравнение
графиков массы (рис.10) и плотности (рис.9) для граничных условий различного
типа позволяет сделать вывод, что к конечному моменту времени расчета в модели
с граничными условия первого типа происходит наибольшая потеря массы, а в
модели с граничными условия третьего типа масса системы, распределение
плотности и давления почти не изменяется.
На основании изложенных выше результатов будем использовать для
дальнейших расчетов граничные условия третьего типа.
13
Рассмотрим теперь задачу о равновесии вращающегося газового шара. Будем
решать систему уравнений (2.1), (2.2), (2.6) с граничными условиями (2.5), (4.7).
Начальные плотность и давление распределены в соответствии с формулами (4.1),
(4.2), газ вращается с угловой скоростью ω. Область  имеет размеры:
r2  z2  1.5l , l = 2.
Известно, что если скорость вращения не велика (то есть энергия вращения
составляет не больше пяти процентов от энергии гравитации), то форма тела
вращения – это эллипсоид, полуоси которого близки по длине [1]. Обозначим
символами K и W энергию вращения и гравитационную энергию:
K
1
2
W

2
r2 d  ,
(4.10)

1
2
   d
.
(4.11)

Проведем серию расчетов, в которых скорость вращения ω будет изменяться
от некого значения ω0 до ω1 (ω0 ≤ ω ≤ ω1), которые выберем из условий:
0:
K 0  0.05 W
1:
K 1  0 .4 W
.
(4.12)
Таким образом, параметром, определяющим скорость вращения в каждом
расчете, является отношение кинетической энергии вращения к гравитационной
энергии. В проводимой серии расчетов этот параметр варьируется от 0.05 до 0.4, а
соответствующая ему скорость вращения изменяется в 2.83 раза.
Во всех расчетах в области  (2.4) строится сетка  (3.3) с числом ячеек
N   50 , а N r  N z  N  50 . Проводились расчеты и при больших N, в частности
при N =100, которые показали, что при увеличении числа ячеек сетки результат
расчета качественно и количественно практически не изменяется.
На рис.11-14 представлена характерная картина течения, в случае, когда
кинетическая энергия вращения составляет 20% от гравитационной энергии, а
скорость вращения ω в 1.99 раза больше ω0. На рис.11, 12 изображены линии
уровня плотности и давления в момент времени t = 66.2, что соответствует
примерно 7 оборотам звезды. На рис.13, 14 изображены линии уровня плотности и
давления в момент времени t = 99.67, что соответствует примерно 10 оборотам
звезды.
Как видно, с течением времени геометрическая форма внешней границы и
линий уровня плотности и давления приобретают форму приближенную к
эллипсоиду. Полуось эллипсоида, лежащая на оси вращения уменьшается по
длине, а радиальная полуось увеличивается. В представленном на рис. 11-14
расчете на конечный момент времени отношение полуосей было равным 0.9.
При увеличении скорости вращения ω отношение длины меньшей полуоси к
большей уменьшается. Так, при скорости вращения ω0 отношение длины меньшей
полуоси к большей на конечный момент времени составляло 0.99, а при скорости
вращения ω1 оно было равным 0.86.
14
Отметим, что начальная конфигурация звезды обладала осевой симметрией,
со временем она остается симметричной относительно оси вращения, при этом
система сохраняет состояние квазиравновесия в течение длительного времени.
5. Заключение.
В настоящей работе путем проведения серии численных экспериментов на
основе трехмерной нестационарной газодинамической модели получены
равновесные конфигурации самогравитирующего газового облака.
Показано, что при решении уравнения Пуассона для гравитационного
потенциала лучше использовать граничные условия интегрального вида (см. стр.
10, формулы 4.7, 4.8), так как в тестовых расчетах оно позволило получить более
точный результат.
Для расчетов создан комплекс программ, реализующий решение уравнения
Пуассона для гравитационного потенциала с различными граничными условиями
на внешней границе и решение уравнений газодинамики, основанное на
разностной схеме Роу, базирующейся на переменных Эйлера.
Найденные равновесные конфигурации могут быть использованы в качестве
начальных данных при численном трехмерном моделировании газодинамических
процессов на поздних этапах эволюции звезд.
Авторы выражают благодарность Абакумову М.В., предоставившему пакет
программ Calculated Data Viewer [15], который использовался нами для анализа
получаемых результатов вычислительного эксперимента.
15
6. Список литературы.
1. Тассуль Ж.Л., “Теория вращающихся звезд”, М. “Наука”, 1982, 472с.
2. Абакумов М.В., Мухин С.И., Попов Ю.П., Чечеткин В.М., “Исследование
равновесных конфигураций газового облака вблизи гравитирующего
центра”, препринт ИПМ им. М.В.Келдыша РАН №33, 1995.
3. Баранов В.Б., “Устойчивость течений в гидроаэромеханике”, Соросовский
образовательный журнал, №9, 1999, c.106-111.
4. Богоявленский
О.И.,
“Автомодельные
адиабатические
движения
самогравитирующего газа в звездах”, Письма в ЖЭТФ, том 27, вып.2, c.9194.
5. Aksenov, A.G., Blinnikov, S.I. “A Newton iteration method for obtaining
equilibria of rapidly rotating stars”, Astronomy and Astrophysics 290, 1994,
p.674-681.
6. Hachisu I., “A versatile method for obtaining structures of rapidly rotating stars”,
The Astrophysical Journal Supplement Series, 61, 1986, p.479-507.
7. Ландау Л.Д., Лифшиц Е.М., “Теория поля ”, М. “Наука”, 1962, 568с.
8. Самарский А.А., Попов Ю.П., “Разностные методы решения задач газовой
динамики”, М. “Наука”, 1992, 423с.
9. Самарский А.А., “Теория разностных схем”, М. “Наука”, 1971, 656с.
10. Самарский А.А., Николаев Е.С., “Методы решения сеточных уравнений”, М.
“Наука”, 1978, 378 с.
11. Дубошин Г.Н., ”Теория притяжения”, М. “Государственное издательство
физико-математической литературы”, 1961, 288 с.
12. Джордж А., Лю Дж., “Численное решение больших разреженных систем
уранений”, М. “Мир”, 1984, 77 с.
13. Гончаров А.Л., “Комплекс программ для решения разреженных систем
алгебраических уравнений”, отчет ИПМ за 1986 г.
14. Кузнецов О.А., “Численное исследование схемы Роу с модификацией
Эйнфельдта для уравнений газовой динамики”, препринт ИПМ им. М.В.
Келдыша РАН №43, 1998.
15. Абакумов М.В., “О некоторых методах визуализации сеточных данных”,
препринт ИПМ им. М.В.Келдыша РАН №72, 2004.
16. Лихтенштейн Л. Фигуры равновесия вращающейся жидкости. // М.:
Наука,1965.
17. Blinnikov, S.I., “Self-consistent field method in the theory of rotating stars”,
Astronomicheskii Zhurnal 52, 1975, p.243-254.
18. Blinnikov, S.I., Sasorov, P.V., Woosley, S.E., “Self-Acceleration of Nuclear
Flames in Supernovae”, Space Science Reviews 74, 1995, p.299-311.
16
Рис.1 Область Ω и подобласть G.
Рис. 2.
17
Рис. 3.
Рис. 4.
18
Рис. 5.
Рис. 6.
19
Рис. 7.
Рис. 8.
20
Рис. 9.
Изменение распределения плотности звезды по радиусу с течением времени
при условии использования в расчете граничных условий для гравитационного
потенциала трех различных типов.
21
Рис. 10.
Изменение массы звезды с течением времени при условии использования в расчете
граничных условий для гравитационного потенциала трех различных типов.
22
Рис. 11.
Рис. 12.
23
Рис. 13.
Рис. 14.