с-2
реклама

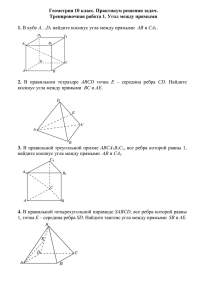
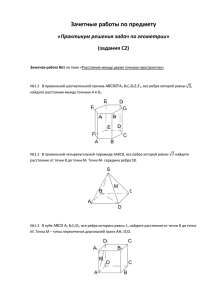
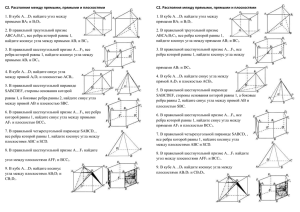
1. 1.В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, найдите расстояние между прямыми SA и BC. Решение: С-2(2) В правильной шестиугольной призме А…F1, все ребра которой равны 1, найдите расстояние от точки А до плоскости BFE1. С-2(3) Все ребра правильной шестиугольной призмы А…F1 равны 1. Найдите косинус угла между прямыми АВ1 и ВС1. С-2(4) В правильной шестиугольной призме А…F1 все ребра которой равны 1, найдите косинус угла между прямыми АВ1 и ВD1 Вершины четырехугольной пирамиды Дана правильная четырехугольная пирамида SABC D, в основании которой лежит квадрат со стороной 1. Боковое ребро BS = 3. Найдите координаты точки S. Решение: Координаты x и y этой точки мы уже знаем: x = y = 0,5. Это следует из двух фактов: Проекция точки S на плоскость OXY — это точка H; Одновременно точка H — центр квадрата ABCD, все стороны которого равны 1. Осталось найти координату точки S. Рассмотрим треугольник AHS. Он пр ямоугольный, причем гипотенуза AS = BS = 3, катет AH — половина диагонали. Для дальнейших вычислений нам потребуется его длина: Теорема Пифагора для 2 2 2 треугольника AHS: AH + SH = AS . Имеем: Итак, координаты точки S: Ответ Угол между двумя прямыми: Задача. В кубе ABCDA1B1C1D1 отмечены точки E и F — середины ребер A1B1 и B1C1соответственно. Найдите угол между прямыми AE и BF. Решение: положим AB = 1. Введем стандартную систему координат: начало в точке A, A = (0; 0; 0) и E = (0,5; 0; 1). B = (1; 0; 0) и F = (1; 0,5; 1), т.к. F — середина отрезка B1C1. Имеем: BF = (1 − 1; 0,5 − 0; 1 − 0) = (0; 0,5; 1). Ответ: arccos 0,8 2. . В правильной трехгранной призме ABCA1B1C1, все ребра которой равны 1, отмечены точки D и E — середины ребер A1B1 и B1C1 соответствен но. Найдите угол между прямыми AD и BE. Решение: Введем систему координат: Ответ: arccos 0,7 Задача. В правильной шестигранной призме ABCDEFA1B1C1D1E1F1, все ребра которой равны 1, отмечены точки K и L — середины ребер A1B1 и B1C1соответственно. Найдите угол между прямыми AK и BL Решение . Введем стандартную для призмы систему координат: начало координат поместим в центр нижнего основания, ось x направим вдоль FC, ось y — через середины отрезков AB и DE, а ось z — вертикально вверх. Единичный отрезок снова равен AB = 1. Выпишем координаты интересующих нас точек: координаты направляющих векторов AK и BL: Точки K и L — середины отрезков A1B1 и B1C1 соответственно, поэтому их координаты находятся через среднее арифметическое. Зная точки, найдем координаты направляющих векторов AK и BL: Теперь найдем косинус угла: Ответ: arccos 0,9