Эконометрика Лабораторная работа №1
реклама

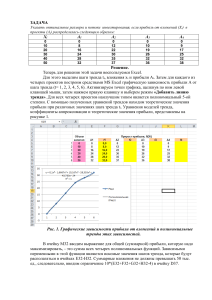
Эконометрика Лабораторная работа №1 Лабораторная работа №1 «Выбор оптимальной аппроксимирующей функции» • Цель работы: Для заданных значений Х и Y найти функцию, которая наиболее точно выражает связь между ними. • Аппроксимация наблюдаемых данных какой-либо математической формулой всегда приближенна. Чем меньше это отличие, тем ближе теоретические (модельные) значения подходят к наблюдаемым, и тем лучше качество модели. Величина отклонений фактических и расчетных значений результативного признака по каждому наблюдению представляет собой ошибку аппроксимации или отклонение. Таким образом, при выполнении задания надо выбрать такую функцию, для которой среднее отклонение будет минимальным. Строим график Y(X) У(Х) 50 45 40 35 30 25 У(Х) 20 15 10 5 0 0 2 4 6 8 10 12 14 Для выделения точечного графика Y(X) надо поставить курсор на одну из точек графика и нажать левую кнопку мыши. Затем, не перемещая курсор, нажать правую кнопку и выбрать в контекстном меню «Добавить линию тренда» После этого появится диалоговое окно: Построить линии тренда (5 штук, кроме линейного фильтра). Для этого: необходимо поставить галочку в строке «Показывать уравнение на диаграмме». Затем на основе уравнения аппроксимации ввести формулу (проставив знаки умножения и заменив Х адресом ячейки, которая этот Х содержит) и рассчитать теоретические значения У для всех значений аргумента Х. На графике добавится линия тренда и формула расчета Y(X) для линейной функции Y(X) 60 50 y = 2.2106x + 19.233 40 Y(X) 30 Linear (Y(X)) 20 10 0 0 2 4 6 8 10 12 14 Для расчета теоретического значения Y по этой функции вводим формулу в соответствующий столбец Отклонение для каждой точки рассчитывается y tyi zi i 100 по формуле: yi где ty – теоретическое значение для соответствующей точки, модуль вычисляется с помощью функции ABS(…). Повторяем аналогичные действия для каждой из пяти функций. • Не следует помещать на одном графике более двух трендов; • Для вычисления экспоненциальной функции ex использовать функцию exp(x); • Для вычисления модуля |x| использовать функцию abs(x) По всем наблюдениям вычисляется среднее отклонение для каждой функции и определяется оптимальная функция аппроксимации (с минимальной погрешностью). Выделите оптимальную функцию другим цветом. n 1 A zi n i 1` Далее каждый студент выполняет индивидуальный вариант задания на основе данных, представленных на листе 3. Номер варианта задания для лабораторной работы № 1 определяется по последней цифре номера зачетной книжки. Например, если номер зачетной книжки Д-11Г10/12, то номер варианта задания равен 2. Если номер зачетной книжки оканчивается на 0 (например, З-3Б10/30), то номер варианта задания равен 10. Таблица 2.